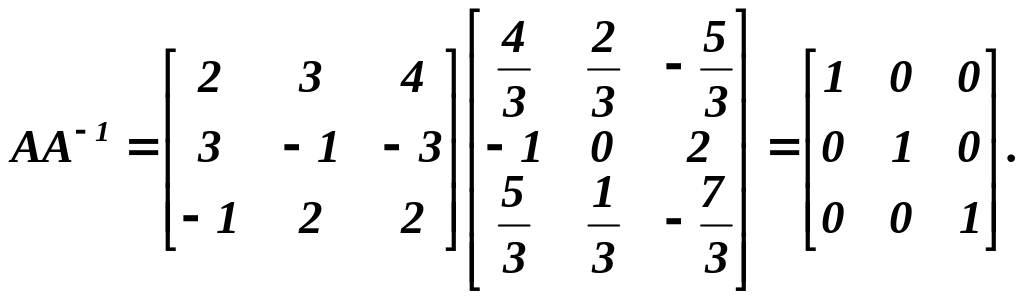§ 6. Обернена матриця

Означення 1. Квадратна матриця го порядку називається невиродженою (або неособливою), якщо її визначник ( ) не дорівнює нулю.

Означення 2.Квадратна матриця го порядку називається виродженою ( або особливою), якщо її визначник дорівнює нулю.

Означення 3. Матриця називається оберненою матрицею для квадратної невиродженої матриці , якщо виконуються рівності

ТЕОРЕМА. Якщо матриця го порядку невироджена, то для неї існує обернена матриця А^-1.

Доведення. Нехай задано квадратну невироджену матрицю , тобто її визначник

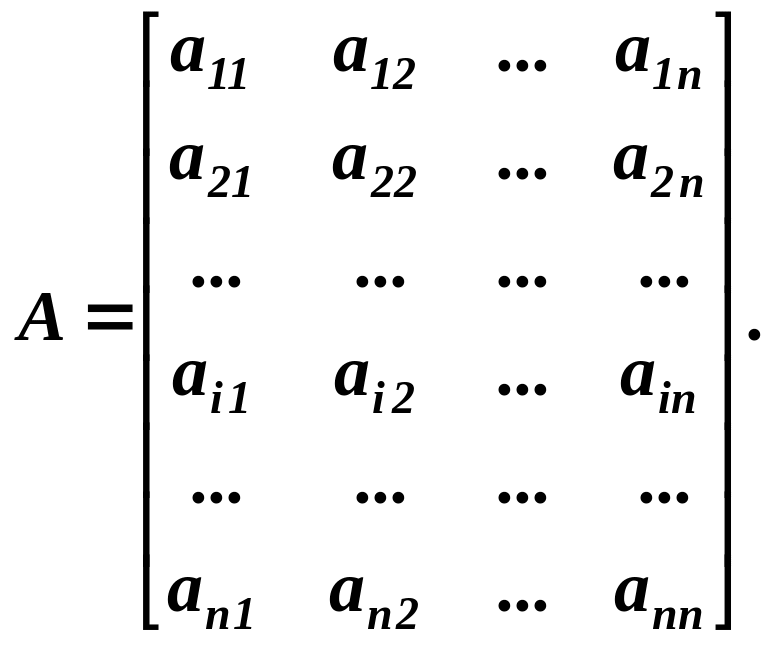
Розглянемо іншу матрицю

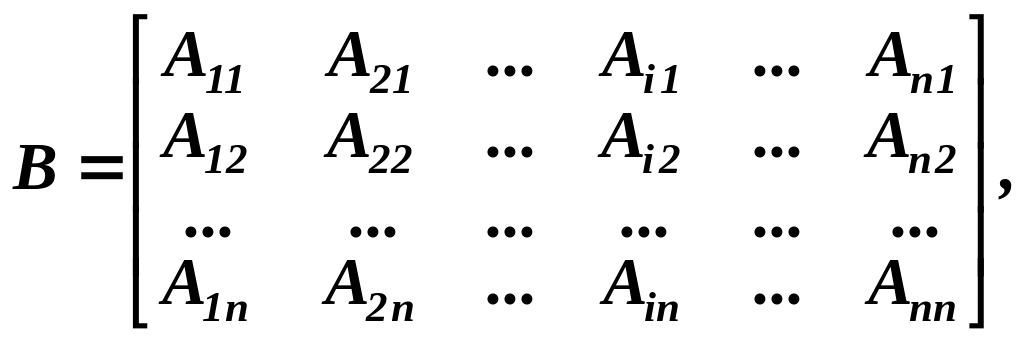
де - алгебраїчні доповнення елементів матриці

Знайдемо добуток АВ:

.

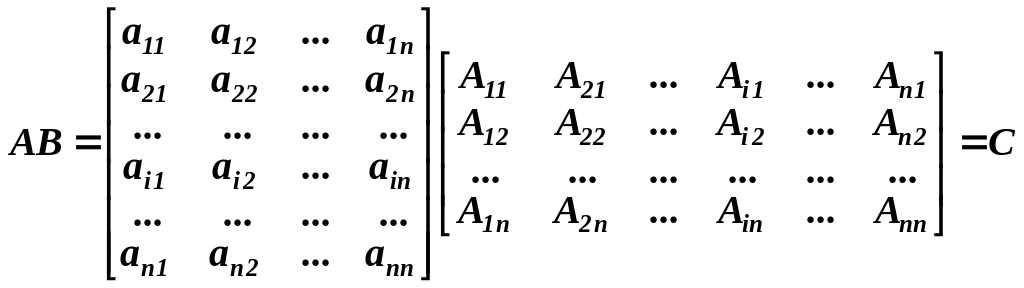Кожен елемент матриці С дорівнює

Якщо то маємо вираз, який є сумою добутків елементів і-го рядка на алгебраїчні доповнення елементів іншого рядка визначника матриці . За теоремою анулювання ця сума дорівнює нулю.

Якщо то вираз представляє собою суму добутків елементів довільного рядка на відповідні алгебраїчні доповнення цього рядка визначника матриці . За теоремою Лапласа така величина дорівнює визначнику матриці ( ).

Тобто матриця С має вигляд:

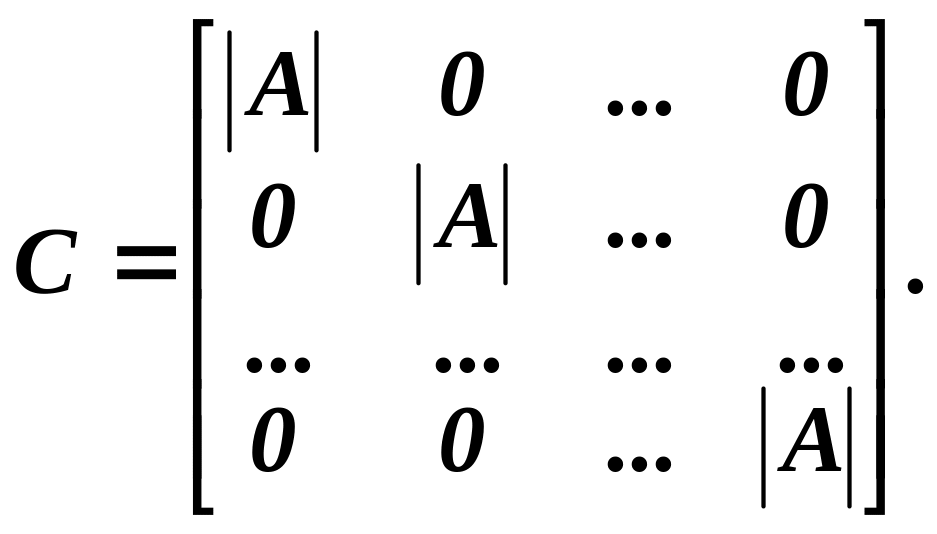
Якщо кожен елемент цієї матриці С розділити на (тобто помножити її на то одержимо одиничну матрицю , тобто

Це доводить теорему.

Отже, обернена матриця має вигляд:

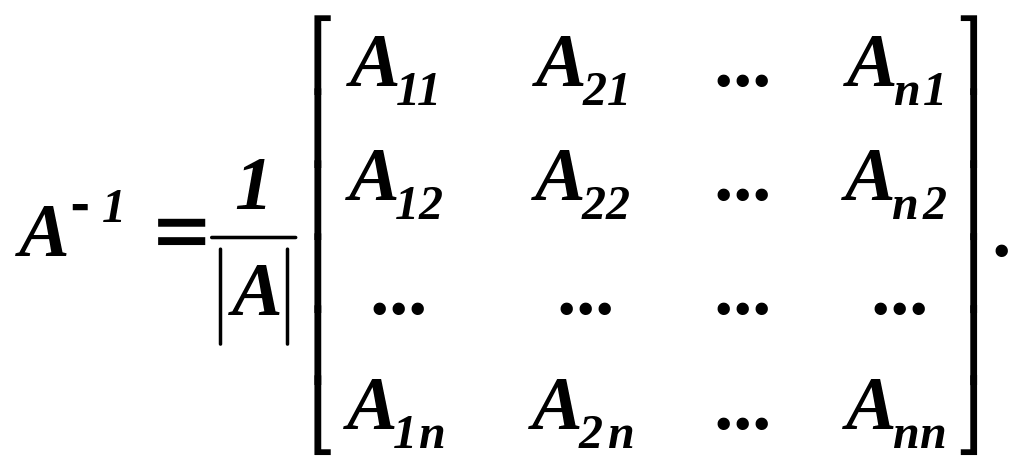
Дамо схему знаходження оберненої матриці для заданої квадратної невиродженої матриці.

1. Обчислимо визначник матриці ).

2. Транспонуємо матрицю , тобто одержуємо матрицю:

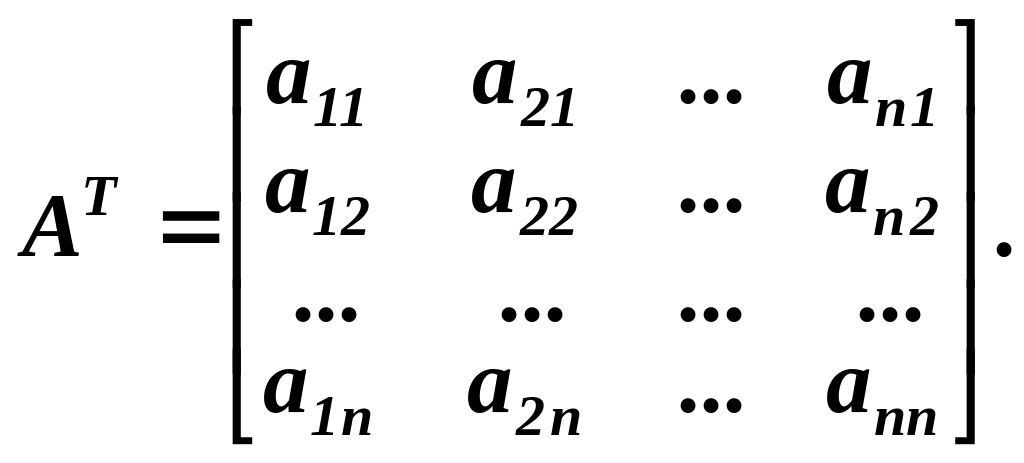
3. Знаходимо алгебраїчні доповнення кожного елемента транспонованої матриці А^Т і запишемо їх у вигляді матриці А^П :

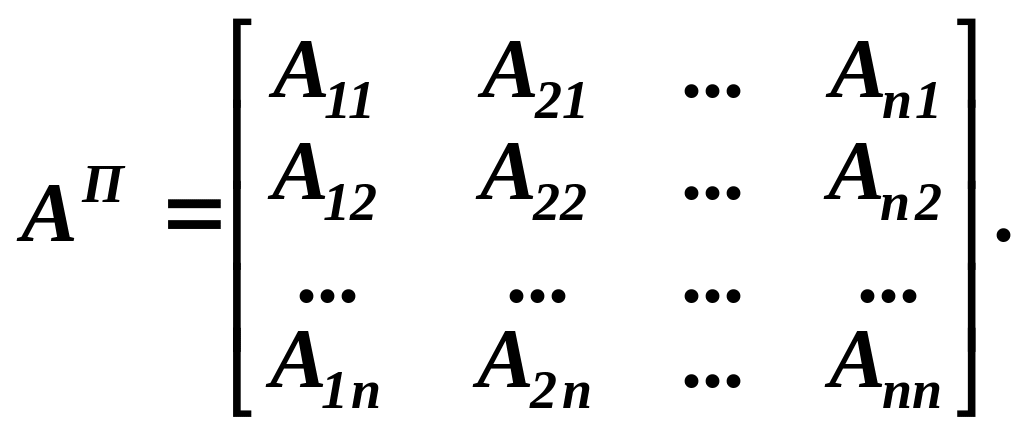
4. Поділимо кожен елемент матриці А^П на визначник матриці

, тобто помножимо число на матрицю . Одержана матриця

буде оберненою:

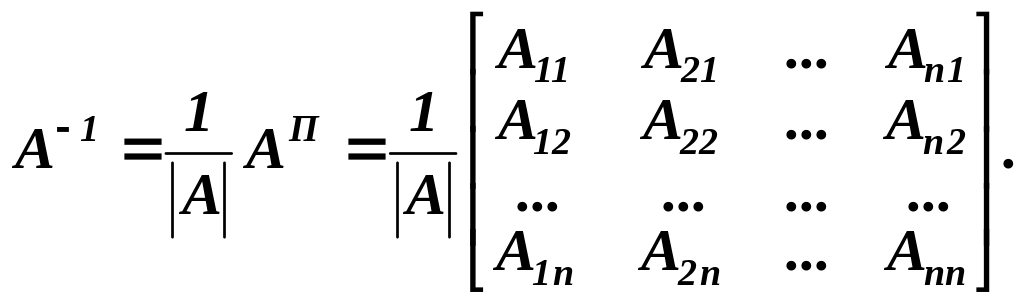
Матриця , яка складена із алгебраїчних доповнень елементів транспонованої матриці, називається приєднаною ( або союзною) до матриці .

Зауваження 1. Приєднана матриця матиме такий же вигляд , якщо транспонувати матрицю, складену із алгебраїчних доповнень елементів матриці .

Приклад 1. Знайти обернену матрицю для матриці

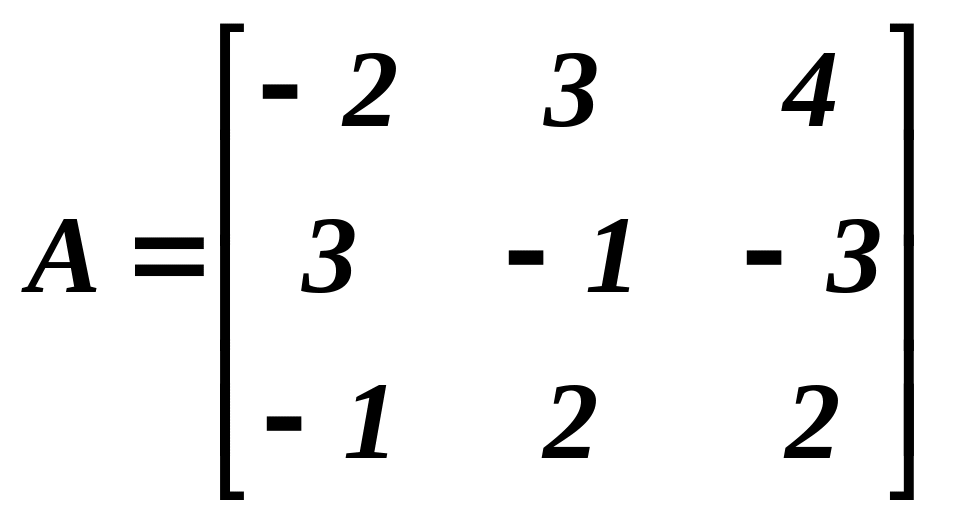
і показати, що

Розв’язування. Визначник цієї матриці

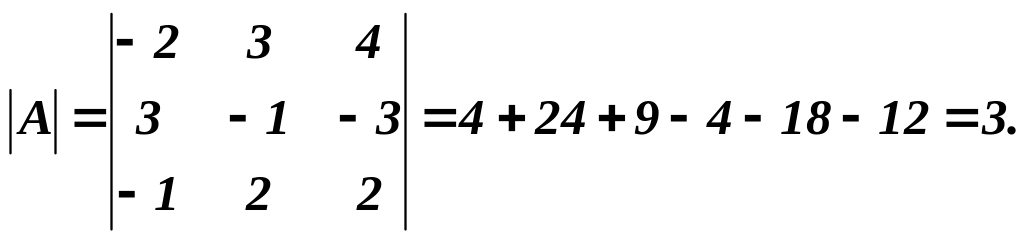
Транспонована матриця має вигляд

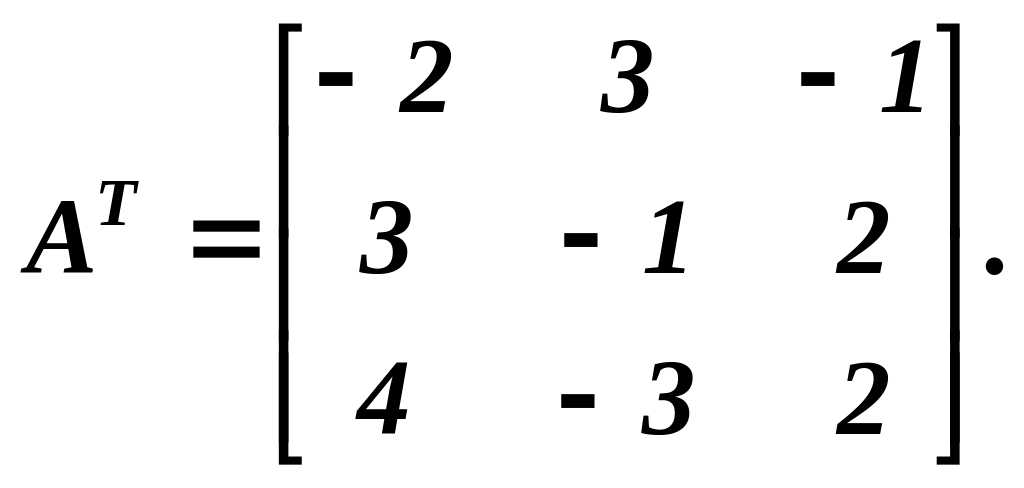
Знайдемо алгебраїчні доповнення кожного елемента цієї матриці

Приєднана матриця буде такою:

Обернена матриця А^-1 для заданої матриці А має вигляд

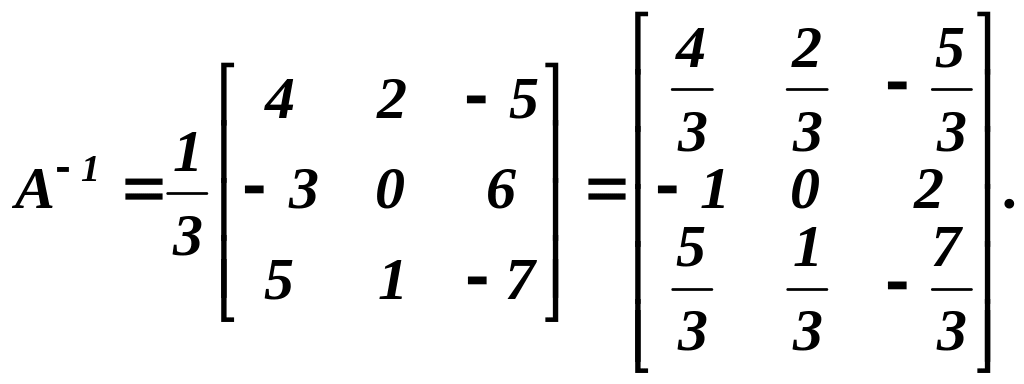
Легко перевірити,що

41