§ 2. Властивості визначників

Визначники довільного порядку мають ряд властивостей.

Властивість 1. Якщо у визначнику поміняти місцями рядки на стовпці, то величина визначника не зміниться:

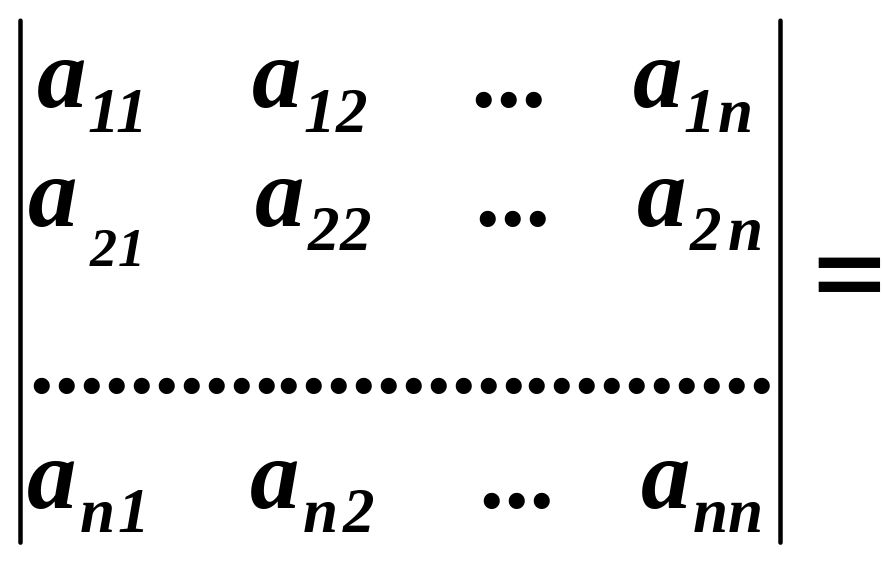
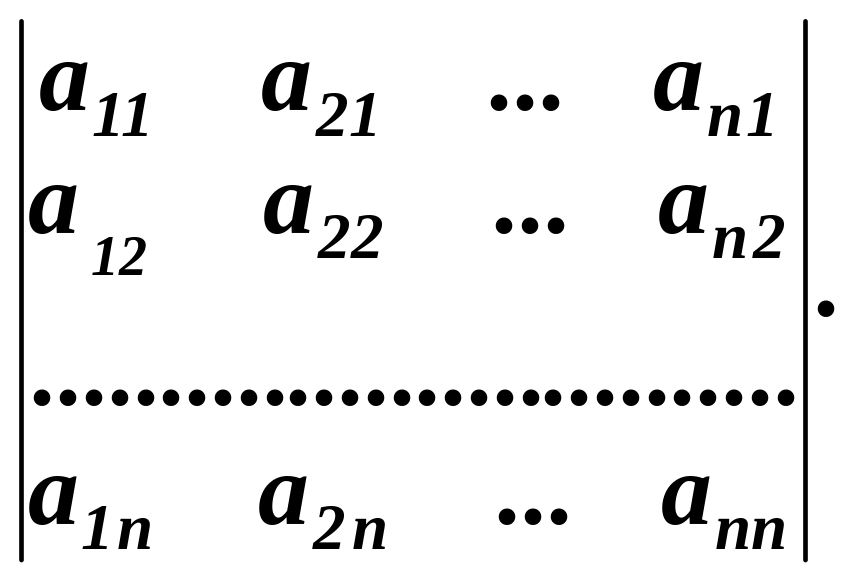
Доведення. Для визначника другого порядку маємо:

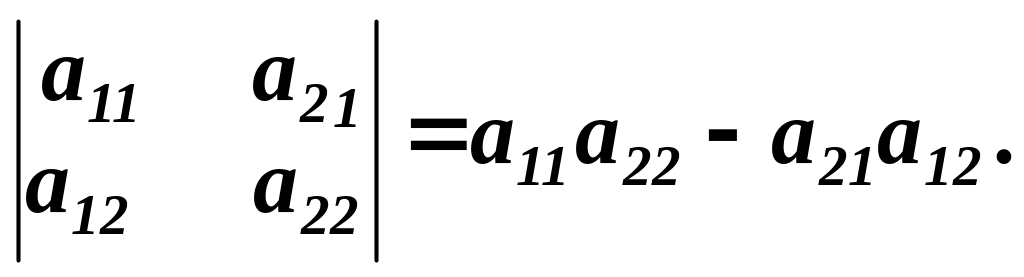
Заміну у визначнику рядків на відповідні стовпці називають

транспонуванням визначника.

Приклад 1. Перевіримо справедливість властивості на

прикладі визначника третього порядку:

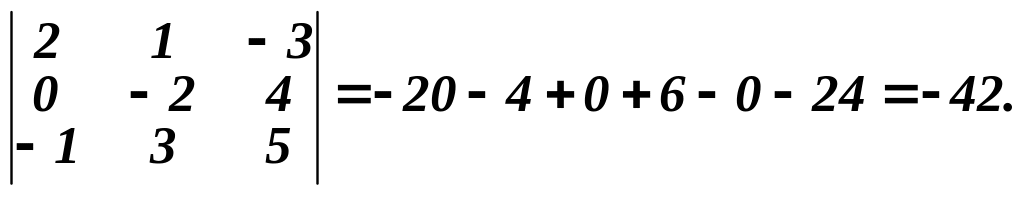
Поміняємо місцями рядки на стовпці:

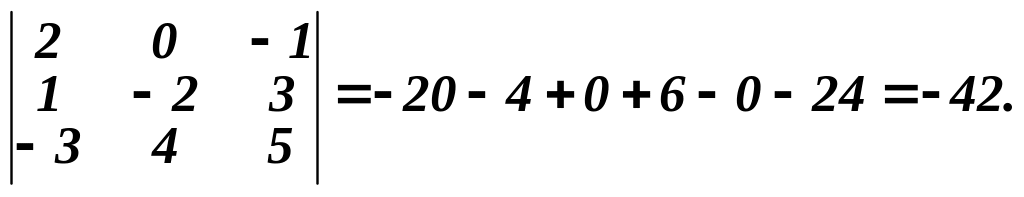
Отже, величина визначника не змінюється при його транспонуванні, тобто його рядки і стовпці рівноправні.

Властивість 2. Якщо у визначнику поміняти місцями два рядки (або стовпці), то він змінить тільки знак, не змінюючи абсолютної величини.

.

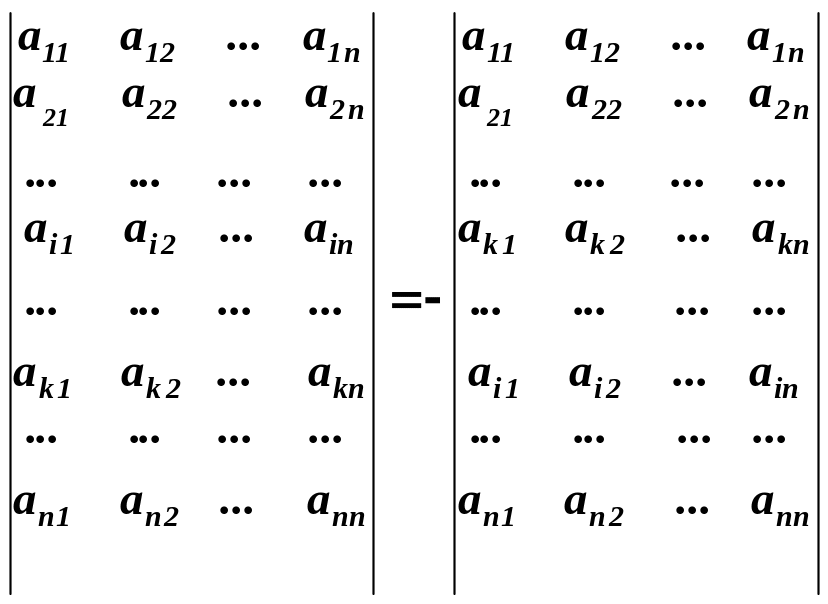Доведення. Поміняємо місцями рядки у визначнику другого порядку:

Приклад 2. Поміняємо місцями перший і третій рядки визначника третього порядку із прикладу 1.

Отже,

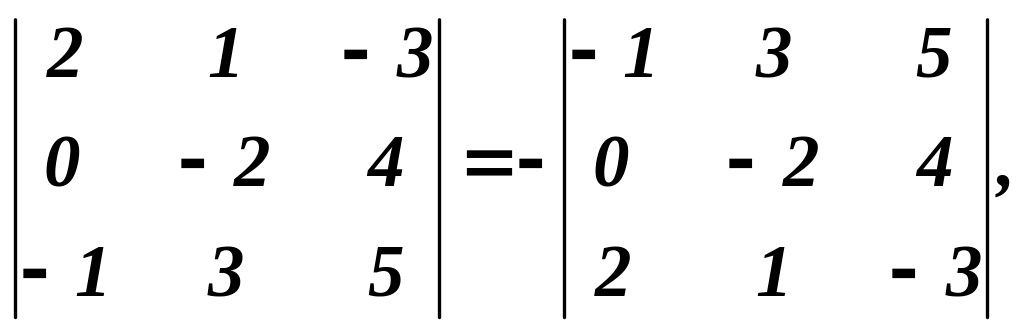
тобто має місце властивість 2.

Властивість 3. Якщо у визначнику всі елементи довільного рядка (або стовпця) дорівнюють нулю, то визначник дорівнює нулю:

і-ий рядок

.

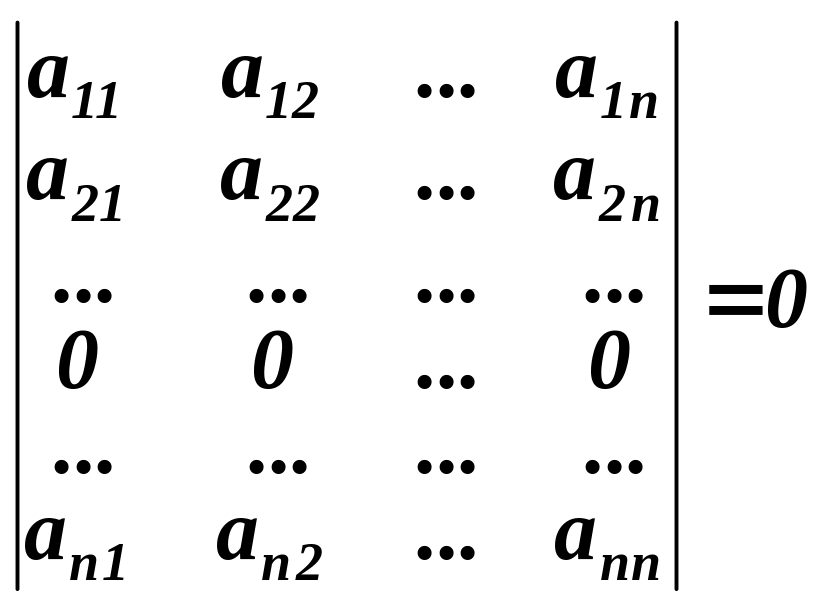
Доведення. Доведення цієї властивості очевидне, оскільки при обчисленні визначника всі доданки містять нульові множники -го рядка. Тому і сам визначник дорівнює нулю.

Властивість 4. Якщо у визначнику є два однакові рядки (або стовпці), то визначник дорівнює нулю.

Доведення. Для доведення цієї властивості поміняємо місцями -ий і ий рядки. З однієї сторони величина визначника не зміниться (оскільки однакові рядки) , а з другої – зміниться знак на протилежний (згідно з властивістю 2). Якщо позначити величину визначника через , то одержимо рівність , тобто , а значить

Приклад 3. Визначник третього порядку дорівнює нулю:

оскільки він має два однакові стовпці.

Властивість 5. Якщо всі елементи довільного рядка (або стовпця) мають спільний множник, то його можна винести за знак визначника:

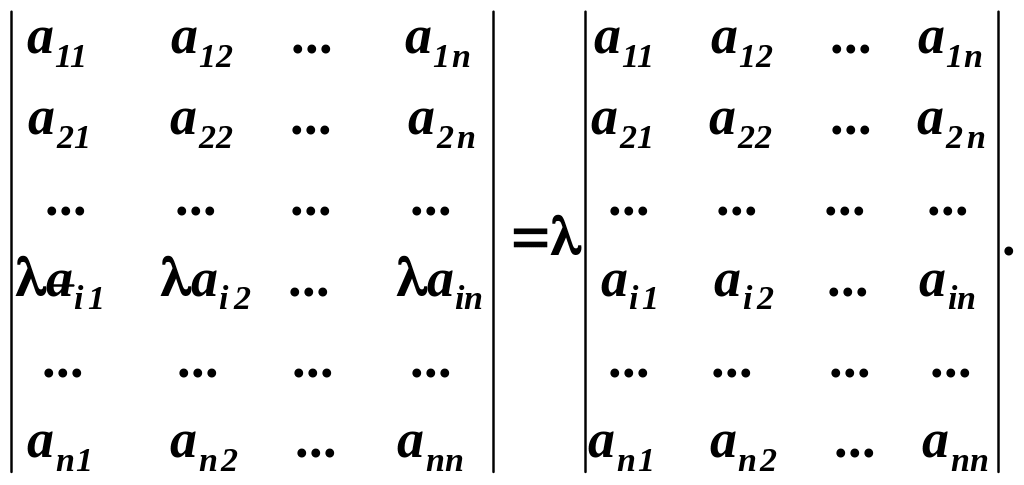
Доведення. Нехай всі елементи -го рядка визначника мають спільний множник λ. Оскільки визначник дорівнює сумі добутків елементів, в т.ч. з розглянутого -го рядка, то можна винести з цієї суми за дужки. Якщо записати вираз в дужках у вигляді визначника, то одержимо попередню рівність.

Наслідок. Якщо довільний рядок (або стовпець) визначника помножити на число λ, то величина визначника зміниться в λ раз.

Зокрема, якщо елементи, наприклад, першого рядка визначника другого порядку мають спільний множник “ ”, то

Приклад 4. У визначнику третього порядку

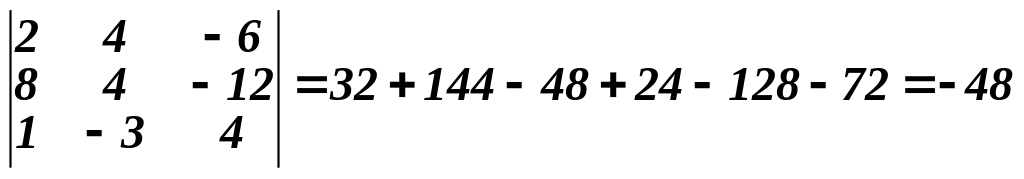
елементи першого і другого рядків мають спільні множники “2” і “4”, тому їх можна винести за знак визначника

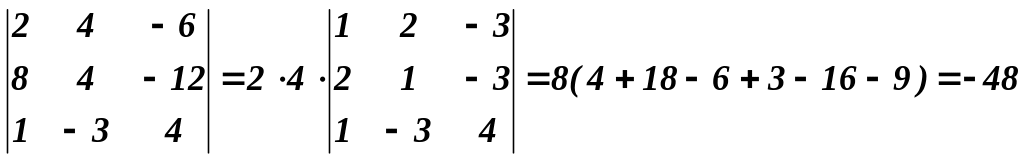
В

ластивість 6. Якщо у визначнику елементи одного рядка (або стовпця) пропорційні відповідним елементам іншого рядка (або стовпця), то визначник дорівнює нулю:

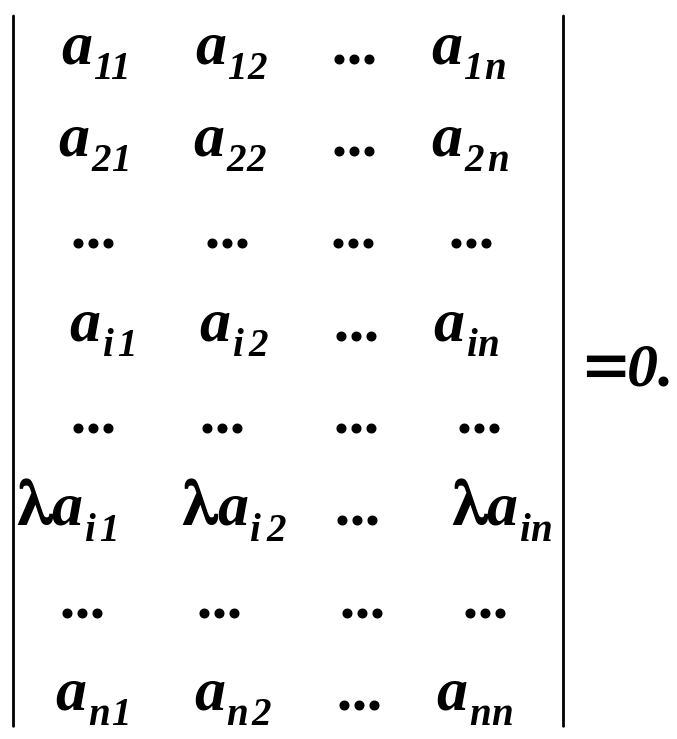
Доведення. Нехай елементи -го і -го рядків пропорційні. За властивістю 5 постійний множник пропорційності λ можна винести за знак визначника. При цьому одержимо добуток числа λ на визначник з двома однаковими рядками, який дорівнює нулю (за властивістю 4).

Приклад 5. Визначник третього порядку

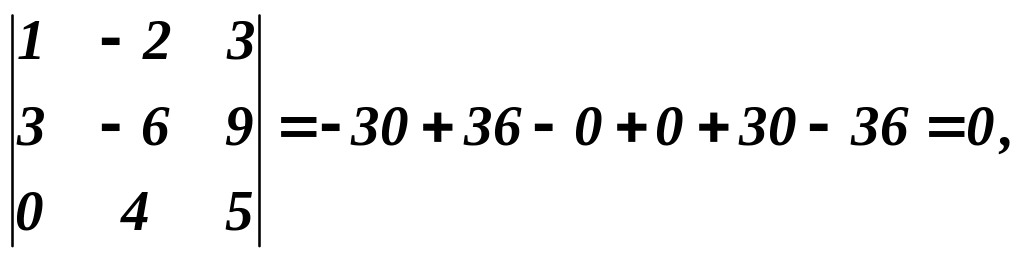
тому що перший і другий рядки пропорційні.

Властивість 7. Якщо у визначнику всі елементи довільного рядка ( або стовпця) є сумою двох доданків, то визначник можна представити у вигляді суми двох визначників. При цьому елементи розглянутого рядка ( або стовпця ) в першому визначнику є першими доданками, а елементи відповідного рядка ( або стовпця) другого визначника - другими доданками:

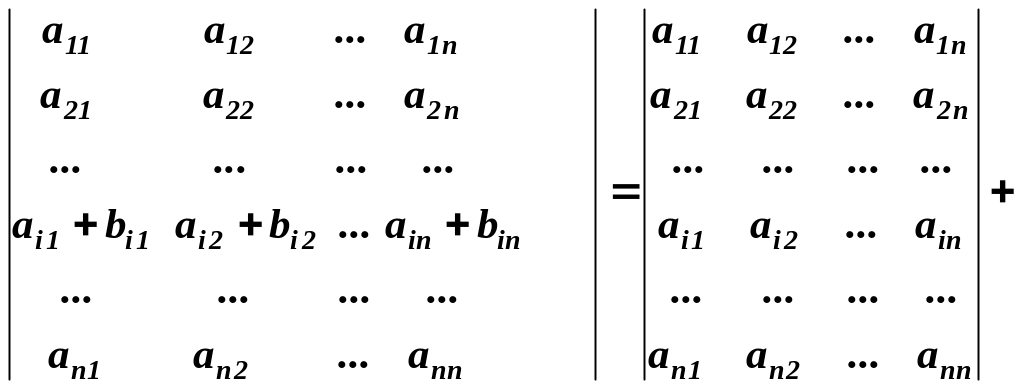
Доведення. Доведемо справедливість цієї властивості на прикладі визначника другого порядку:

Приклад 6. Обчислити визначник:

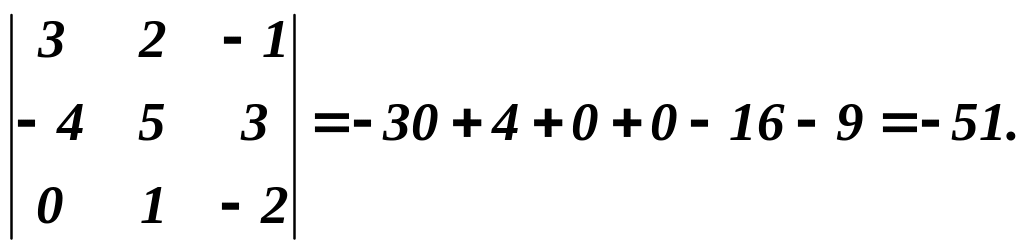
Елементи, наприклад, другого рядка можна представити у вигляді суми двох доданків:

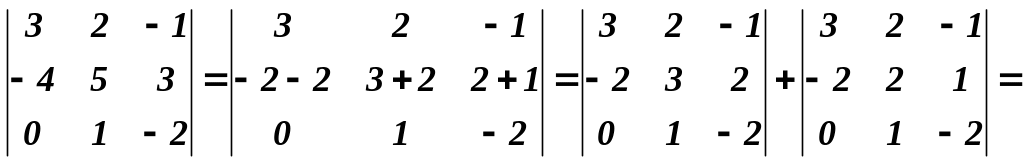
Властивість 8. Величина визначника не зміниться, якщо до

елементів довільного рядка (або стовпця) додати відповідні елементи іншого рядка (або стовпця), помножені на одне і те ж число :

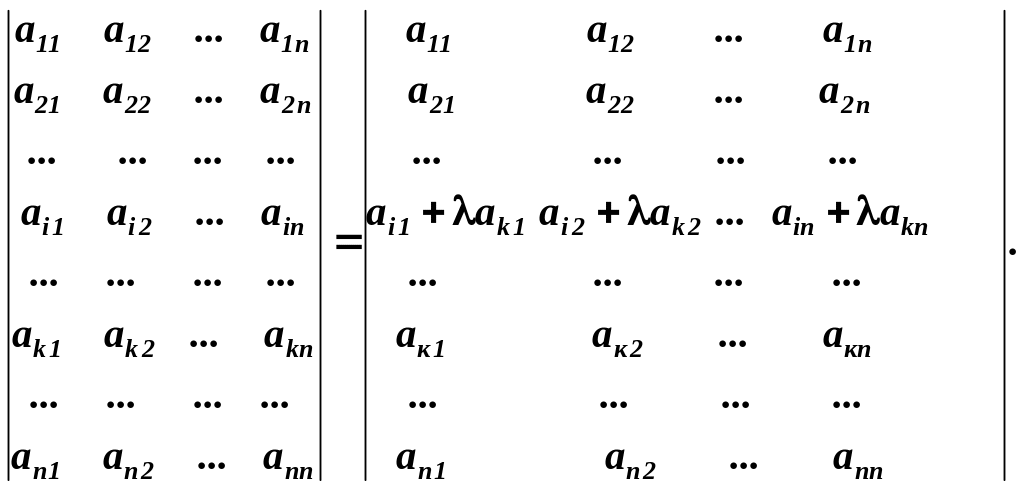
Доведення. Для доведення представимо визначник правої частини згідно з властивістю 7 у вигляді суми двох визначників:

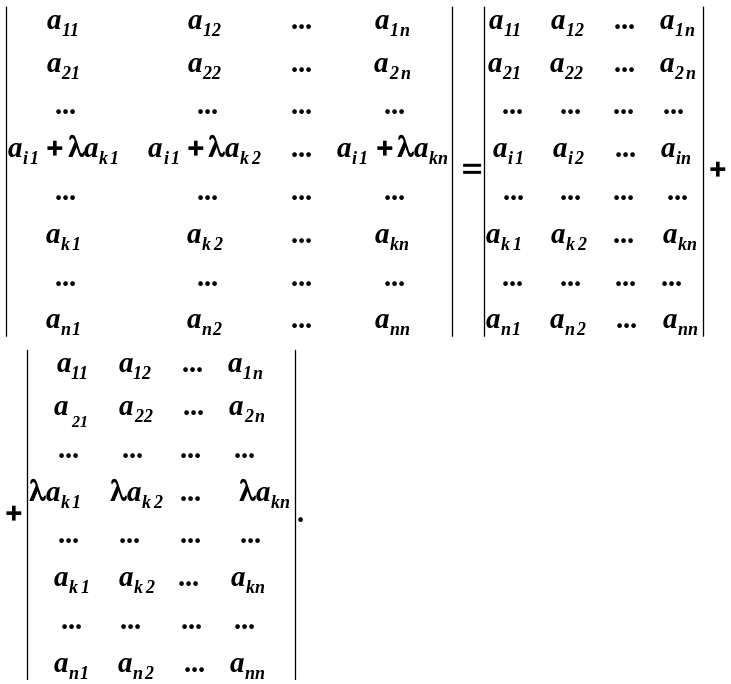
В другому визначнику правої частини елементи і-го рядка пропорційні відповідним елементам k-го рядка, тому за властивістю 6 такий визначник дорівнює нулю. Отже, має місце властивість 8.

Приклад 7. Обчислити визначник

Тут ми до елементів третього рядка додали відповідні елементи першого рядка, помножені на число “-3”.

Надалі, властивість 8 використовується для обчислення визначників вищих порядків. При цьому в довільному рядку ( або стовпці) утворюємо всі нулі, крім одного елемента.

Нехай маємо визначник го порядку ( ;

.

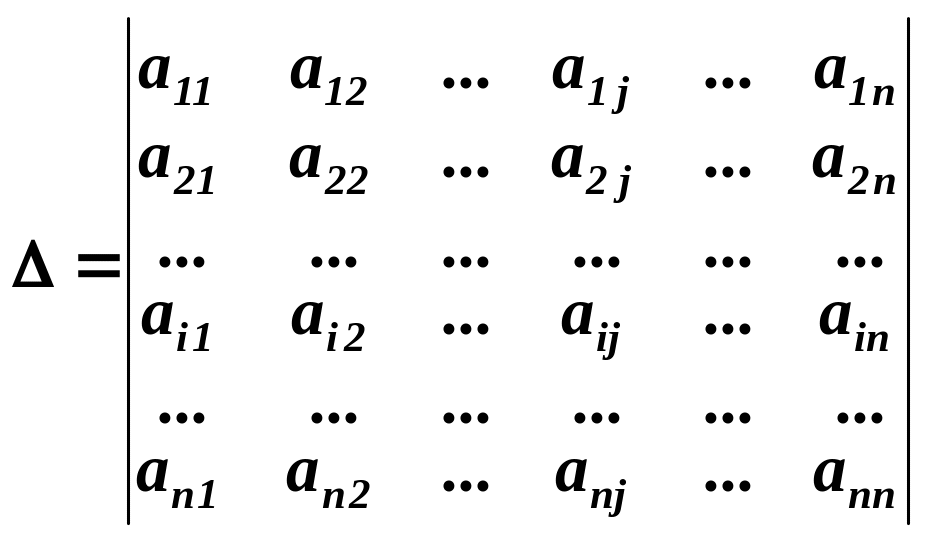Означення 1. Мінором елемента визначника го порядку називається визначник го порядку, одержаний із попереднього після викреслювання го рядка і го стовпця, на перетині яких знаходиться даний елемент.

Означення 2. Алгебраїчним доповненням елемента визначника го порядку називається мінор для цього елемента, взятий із знаком “+”, якщо число - парне та із знаком “-”, якщо воно непарне. Тобто .

Приклад 8. Знайти алгебраїчні доповнення до елементів та визначника .

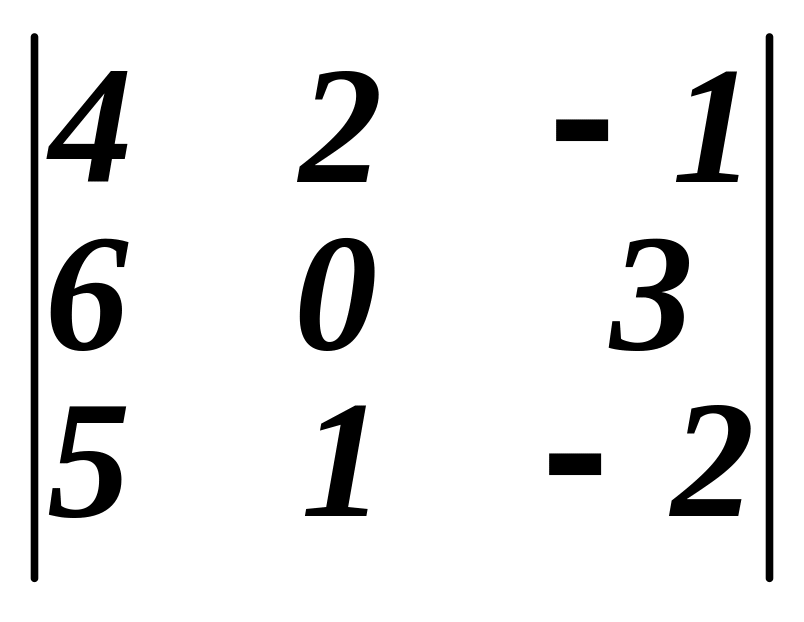Алгебраїчні доповнення A₁₃ і A₃₂ знайдемо за попередньою формулою:

;

Згідно з означенням 1 маємо:

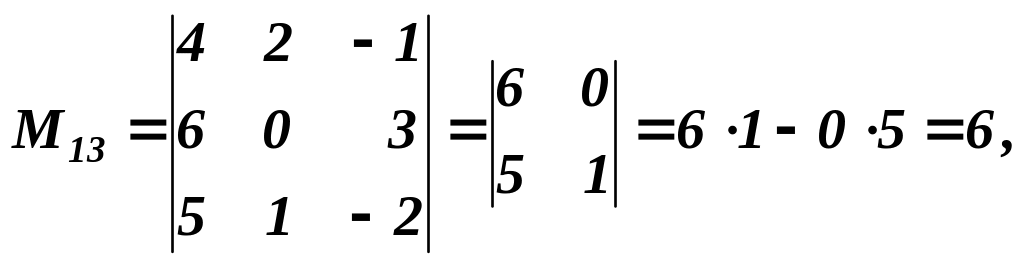
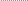
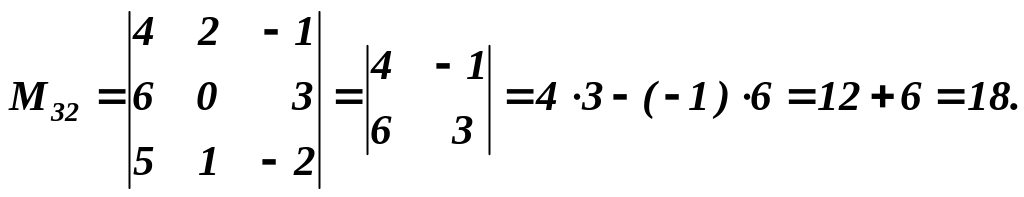
Шукані алгебраїчні доповнення будуть

Властивість 9. (Теорема Лапласа).

Визначник дорівнює сумі добутків елементів довільного рядка (або стовпця) на відповідні алгебраїчні доповнення:

(1.1)

Ця теорема називається ще теоремою розкладу. При цьому перша формула є розкладом визначника за елементами його рядка, а друга - розкладом визначника за елементами його стовпця.

Доведення. Доведемо цю властивість для визначника третього порядку:

Однак,

Таким чином,

Це формула розкладу визначника за елементами першого рядка. Аналогічно можна знайти розклад визначника за елементами іншого рядка або довільного стовпця.

З допомогою цієї властивості, обчислення визначника го порядку зводиться до обчислення визначників - го порядку. Тому при обчисленні таких визначників найкраще вибирати для розкладу рядок або стовпець, в якому є нулі. При цьому будемо обчислювати не визначників - го порядку, а менше.

Приклад 9. Обчислити визначник 3-го порядку , розклавши його за елементами першого рядка:

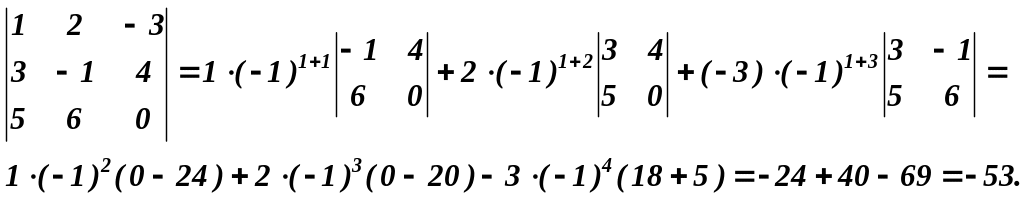Зауваження. Даний визначник простіше було б обчислювати, розклавши його за елементами третього рядка (або третього стовпця), оскільки один із доданків не потрібно обчислювати (елемент ).

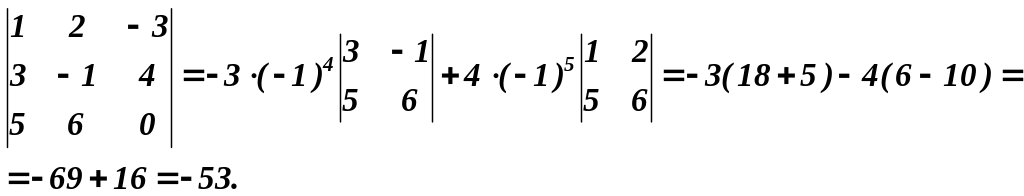Наслідок 1 (Теорема заміщення).

Нехай - алгебраїчні доповнення елементів -го

рядка визначника го порядку

Тоді сума добутків алгебраїчних доповнень елементів і-го рядка на довільні числа b₁, b₂,…, b_n дорівнює такому визначнику го порядку , в якого елементами -го рядка є числа b₁, b₂,…, b_n, а інші - співпадають з відповідними елементами визначника .

Доведення. За теоремою маємо, що

.

Тут

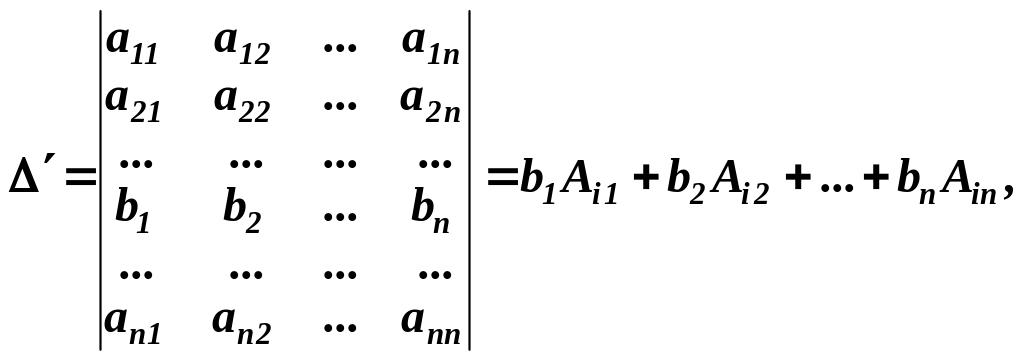
де права частина одержалась після розкладу визначника го порядку за елементами -го рядка. Це і доводить теорему.

Аналогічно, сума добутків алгебраїчних доповнень елементів го стовпця на довільні числа , тобто дорівнює визначнику , елементами го стовпця якого є числа , а інші елементи співпадають з відповідними елементами визначника .

Наслідок 2 (Теорема анулювання).

Сума добутків елементів довільного рядка (або стовпця) на алгебраїчні доповнення паралельного іншого рядка (або стовпця) дорівнює нулю.

Д

оведення. У визначнику виділимо два рядки -ий і -ий.

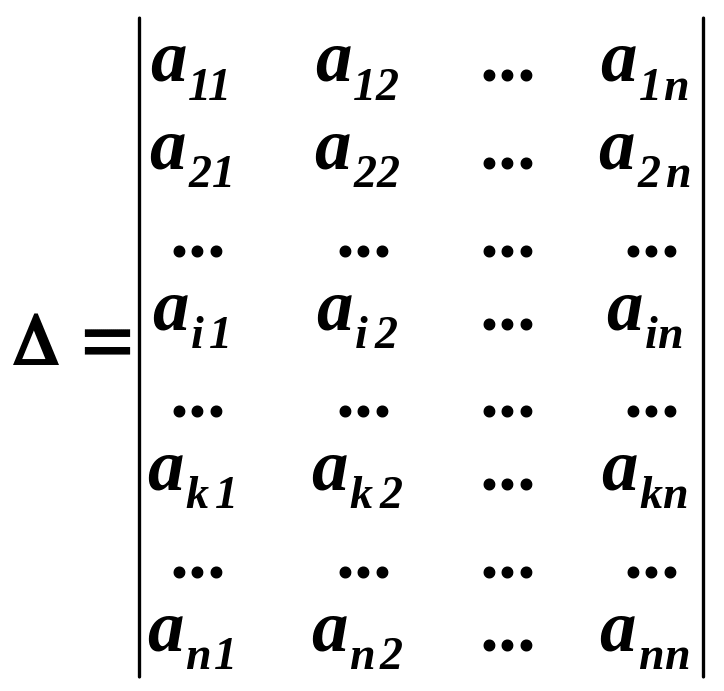
Знайдемо суму добутків елементів

-го рядка на алгебраїчні доповнення елементів -го рядка:

За теоремою заміщення цю суму можна замінити визначником з двома однаковими рядками

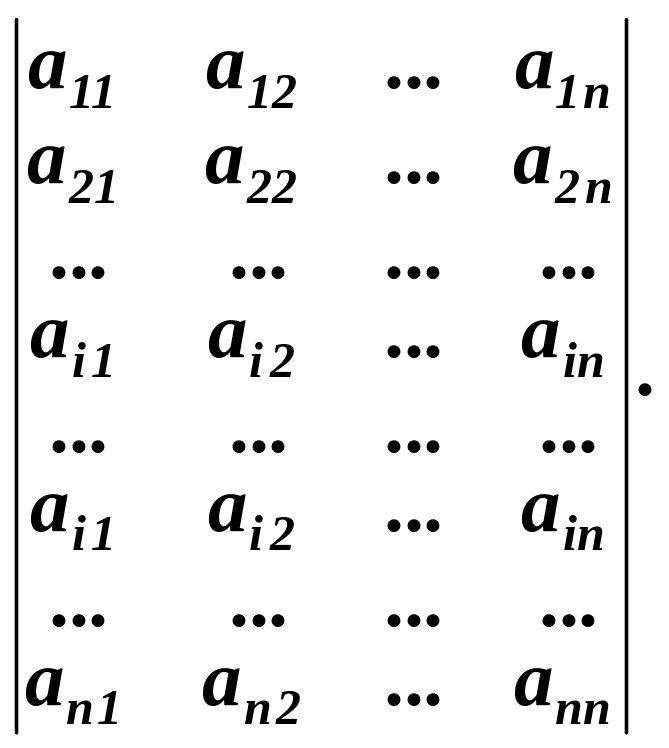
Одержаний визначник має два однакові рядки, а тому дорівнює нулю.

Приклад 10. Користуючись властивостями визначників, обчислити

Розв’язування. Додамо елементи першого і другого стовпців, а від елементів третього стовпця віднімемо подвоєні елементи першого. Одержимо:

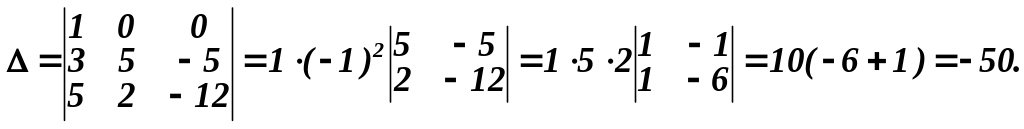Приклад 11. Обчислити визначник, використавши його властивості:

Розв’язування. Винесемо за знак визначника спільний множник “8” першого стовпця і спільний множник “7” другого рядка

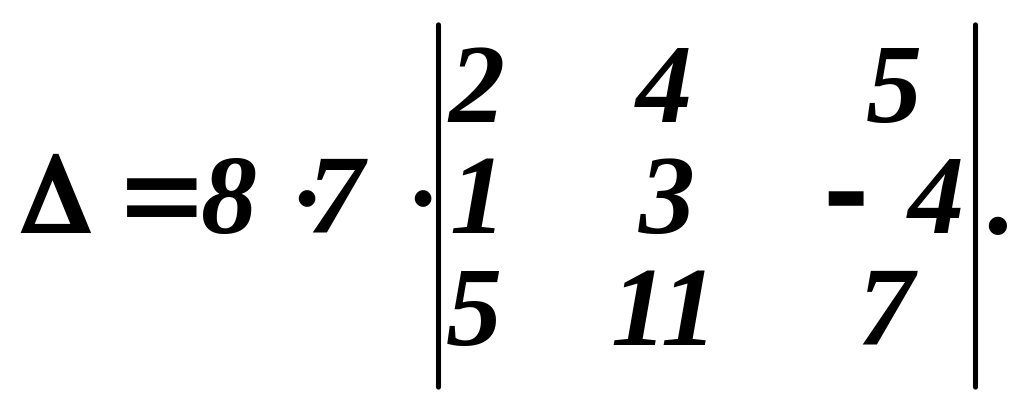
Віднімемо від елементів першого рядка подвоєні відповідні елементи другого рядка. До елементів третього рядка додамо відповідні елементи другого рядка, помножені на число “-5”

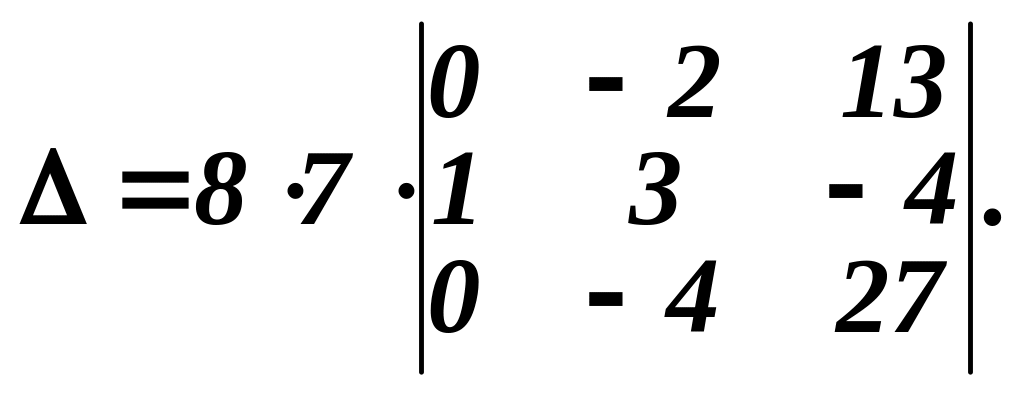
Такий визначник легко обчислити, розклавши його за елементами першого стовпця: