Розділ 1. Елементи лінійної алгебри

§1. Поняття визначника. Визначники другого і третього порядків

Розв’язування багатьох економічних задач зводиться до розв’язування систем лінійних алгебраїчних рівнянь. В основі деяких методів розв’язування таких систем використовуються вирази, які називаються визначниками ( або детермінантами).

Розглянемо квадратну таблицю з чисел, розміщених в - горизонтальних і -вертикальних рядах. За спеціальними правилами знаходиться число, яке називають визначником -го порядку і позначають буквою грецького алфавіту:

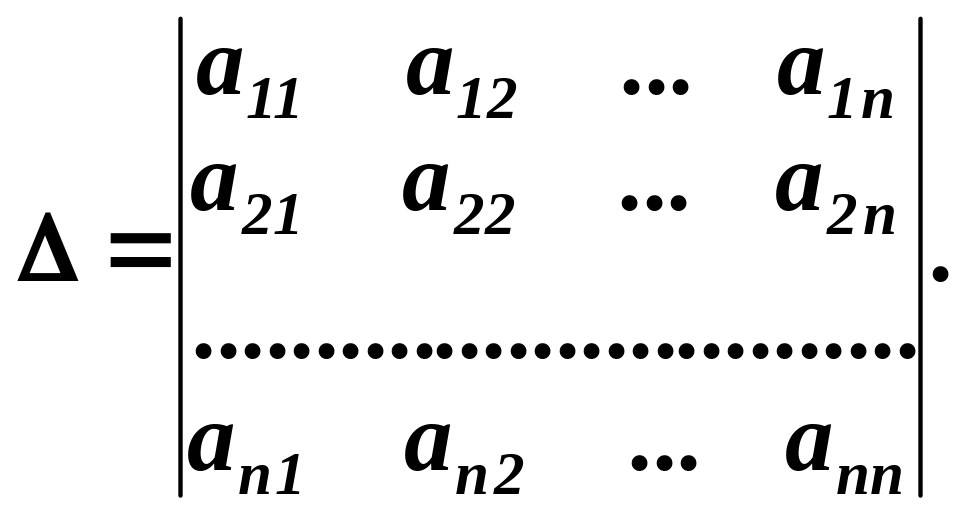
Числа - називають елементами

визначника. Перший індекс вказує номер рядка, а другий – номер стовпця, на перетині яких знаходиться елемент. Елементи, в яких обидва індекси однакові (тобто елементи утворюють головну діагональ визначника. Інша діагональ називається неголовною (допоміжною). Порядок визначника визначає кількість його рядків (або стовпців).

При обчисленні визначників -го порядку одержуємо число, яке дорівнює алгебраїчній сумі всіх можливих добутків його еле-ментів, взятих по одному з кожного з рядків і кожного із стовпців. При цьому половина доданків мають свої знаки, а інша - протилежні.

Покажемо, як обчислюються визначники другого і третього порядків. Для уточнення поняття “визначник” розглянемо два лінійних рівняння з двома невідомими з буквеними коефіцієнтами:

Для розв’язування цих рівнянь ми повинні помножити їх на

відповідні коефіцієнти, при яких виключається одне з невідомих:

В залежності від використаної пари множників ( по вертикалі) виключаємо або або і отримаємо такі рівняння:

Звідси

.

Ці вирази мають зміст тільки при умові, якщо знаменник не дорівнює нулю.

Якщо, то система рівнянь або немає розв’язку , або має нескінченну множину розв’язків. Коефіцієнти при невідомих утворюють вирази, які називаються визначниками.

Розглядаючи ці коефіцієнти, ми бачимо, що вони однакові при обох невідомих; складаються з двох добутків,кожний з яких включає два елементи.

Визначники другого порядку символічно позначаються так:

.

Визначником другого порядку називається число, яке дорівнює різниці добутків елементів головної і допоміжної діагоналей, тобто .

Ц е ілюструється схемою:

Приклад 1. Обчислити визначник другого порядку:

Розв’язування. За попередньою формулою знаходимо:

Визначником третього порядку називається число, яке знаходиться за формулою

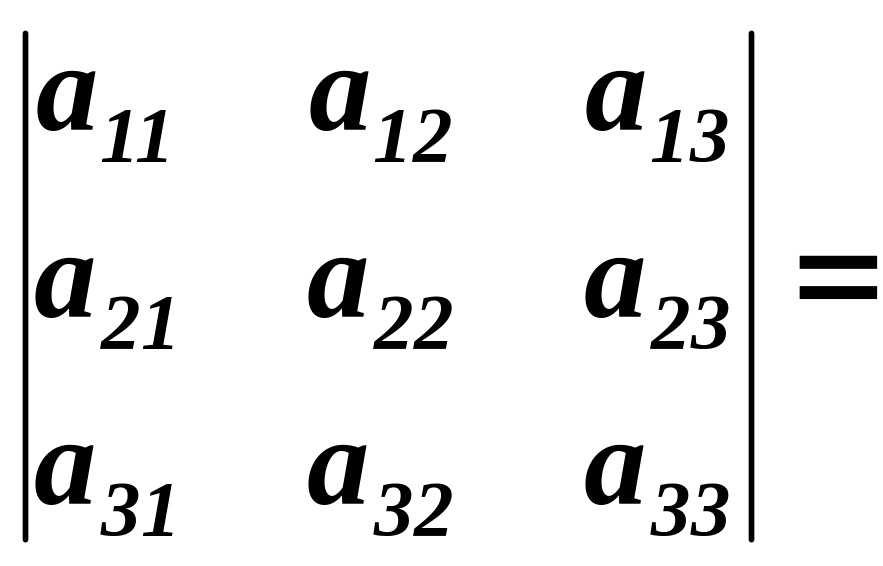
Знаки, які стоять перед кожним із доданків, слід вибирати з такої схеми:

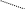
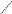
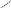
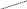
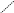
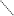
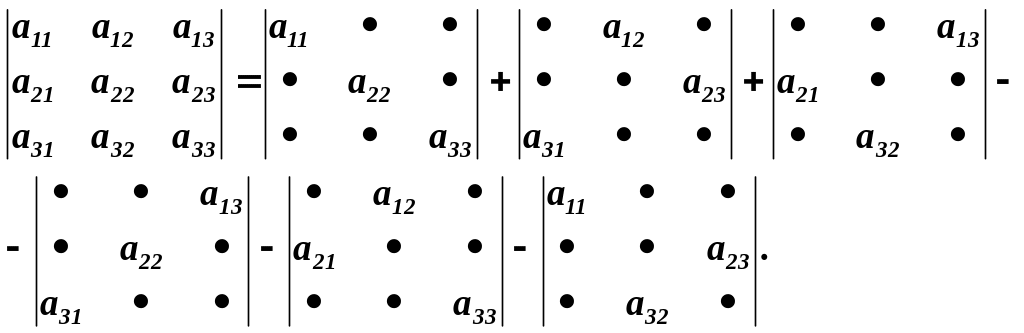
Це правило обчислення визначників 3-го порядку називається правилом трикутників. Тут доданки із знаком “+” є добутками елементів, які стоять на головній діагоналі визначника і добутки елементів, які стоять у вершинах трикутників з основами паралельними головній діагоналі і . Із знаком “-” беруться доданки, які є добутками елементів неголовної діагоналі і добутки елементів вершин трикутників із основами, паралельними цій діагоналі визначника: і .

Приклад 2. Обчислити визначник .

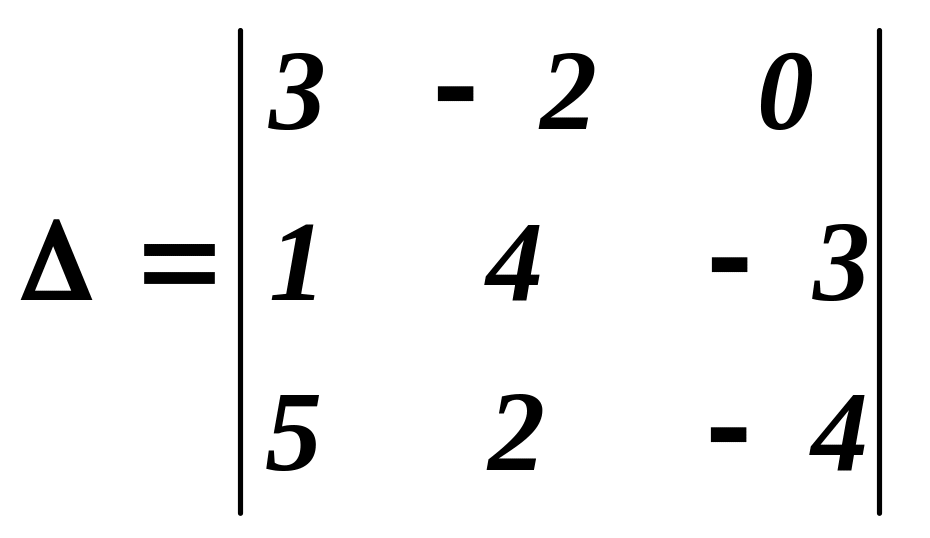Розв’язування. Користуючись правилом трикутників,

одержимо

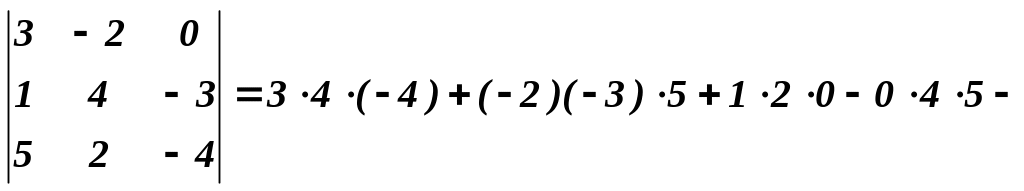
Правило трикутників легко запам’ятати, якщо дописати поряд з визначником перший, а потім другий його стовпці. Добутки елементів, які знаходяться на діагоналях, відмічених на схемі суцільними лініями, беруться із знаком “+”, a добутки елементів, які знаходяться на діагоналях, позначених на схемі пунктиром, із знаком

“-”. Алгебраїчна сума цих шести добутків і дає значення визначника

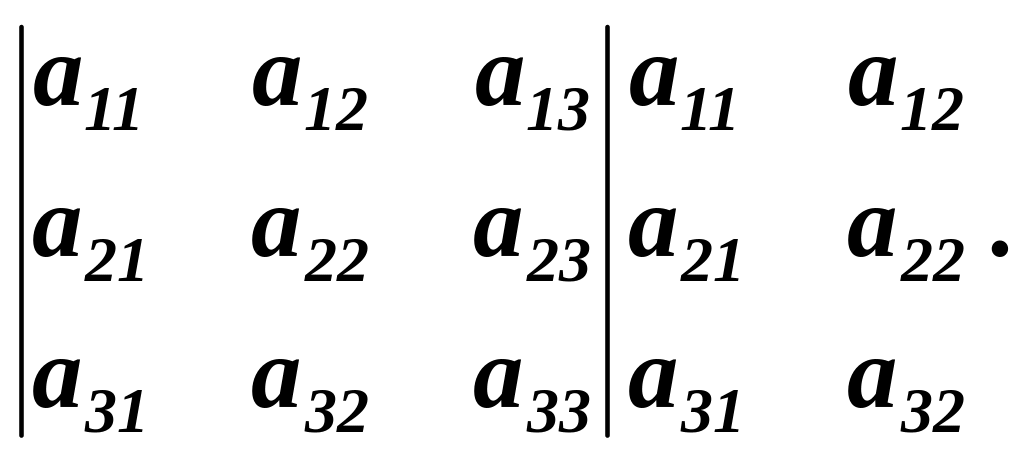
Такий спосіб обчислення визначника третього порядку називається правилом Саррюса.

Обчислимо попередній визначник 3-го порядку за

правилом Саррюса.

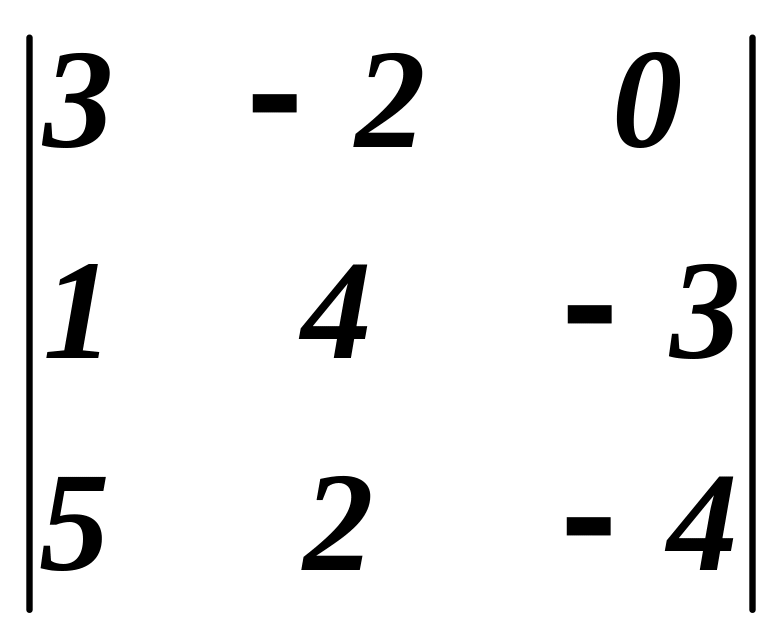
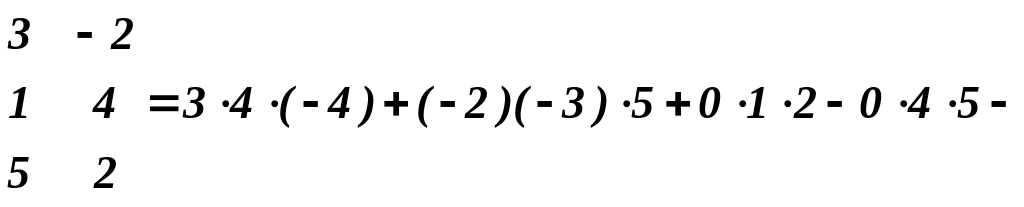
При обчисленні визначників використовують їх властивості, які розглядаються в наступному параграфі.

Зауваження. Визначником першого порядку є число, яке дорівнює цьому елементу, тобто а₁₁= а₁₁. Тому не слід плутати позначення визначника з модулем самого числа.