МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

ПОЛТАВСЬКИЙ НАЦІОНАЛЬНИЙ ТЕХНІЧНИЙ УНІВЕРСИТЕТ ІМЕНІ ЮРІЯ КОНДРАТЮКА

Кафедра Залізобетонних і кам’яних конструкцій

та опору матеріалів

Методичні вказівки та завдання

до розрахунково-проектувальної роботи з курсу "Опір матеріалів" (спецкурс „Теорія пружності”) на тему ”Кручення тонкостінних стрижнів” для студентів будівельних спеціальностей

денної та заочної форм навчання

Полтава 2008

Методичні вказівки та завдання до розрахунково-проектувальної роботи з курсу "Опір матеріалів" (спецкурс „Теорія пружності”) на тему ”Кручення тонкостінних стрижнів” для студентів будівельних спеціальностей денної та заочної форм навчання. – Полтава: ПолтНТУ, 2006. – 14 с.

Укладачі: Р.В. Толстопятов, кандидат технічних наук, доцент;

В.А. Кириченко, кандидат технічних наук, асистент.

Відповідальний за випуск: В.В. Муравльов, кандидат технічних наук, доцент.

Рецензент: О.Г. Фенко, кандидат технічних наук, доцент.

Затверджено радою університету

Протокол № 3 від 23.03. 2006 року

Редактор Я.В. Новічкова

Коректор Н.О.Янкевич

Зміст

Загальні відомості 4

Послідовність роботи та рекомендації щодо її виконання 7

Контрольні запитання 13

Література 13

Варіанти завдань 14

Додаток 16

Загальні відомості

Робота виконується для закріплення теоретичних знань з розділу "кручення тонкостінних стрижнів" та здобування практичних навичок при визначенні їх міцності.

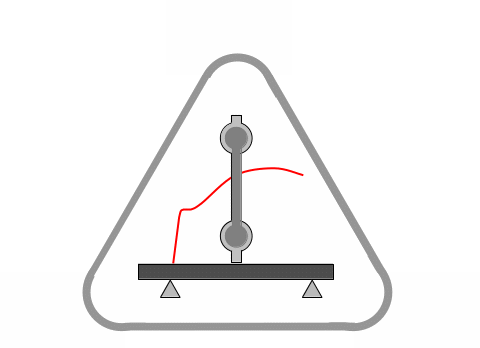
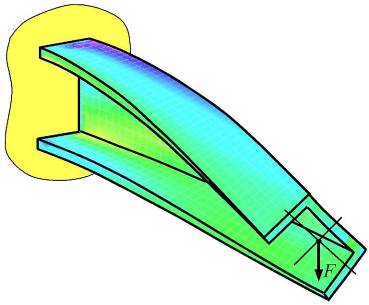
Тонкостінними називають стрижні, в яких товщина перерізу значно менше за габаритні розміри контуру. Ці розміри у свою чергу значно менші, ніж довжина стрижня . Тонкостінними можуть бути стрижні відкритого і закритого профілів.

Рис. 2.1

Опір тонкостінних стрижнів (особливо відкритого профілю) зовнішнім навантаженням у деяких випадках суттєво відрізняється від опору стрижнів суцільного перерізу. Справа в тому, що в тонкостінних стрижнях не завжди виконується гіпотеза плоских перерізів, тобто може виникати депланація – викривлення плоского перерізу під час деформації. Це у свою чергу призводить до появи додаткових напружень. Розрізняють вільне та обмежене кручення тонкостінних стрижнів. Вільне кручення відбувається, якщо немає ніяких перешкод для депланації перерізів. Тому всі перерізи деплануються однаково і додаткових напружень не виникає.

Обмежене кручення виникає, якщо всі або деякі перерізи не можуть вільно деплануватись. Узагалі, наявність будь-якої опори вже накладає обмеження на депланацію перерізів. Якщо різні перерізи деплануються по-різному, то в поздовжніх волокнах виникають додаткові деформації та відповідно нормальні напруження.

Для визначення напружено-деформованого стану тонкостінних стрижнів виникає потреба в застосуванні ще деяких, крім уже відомих, геометричних характеристик перерізів. При цьому використовуються дві фіксовані точки – полюс і нульова точка , яка розташована на профілі контуру.

Секторіальна координата точки (або секторіальна площа) – це подвійна площа сектора, який окреслюється початковим положенням радіус-вектора , контуром профілю та радіус-вектором самої точки .

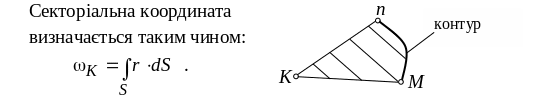
Якщо профіль утворено прямими лініями, то ця площа підраховується без застосувань інтегралів як площа трикутника. Додатною вважається координата, якщо рух радіус-вектора відбувається проти годинникової стрілки.

Розрізняють такі секторіальні геометричні характеристики:

– секторіальний статичний момент;

– секторіальний момент інерції;

, – лінійно-секторіальні статичні моменти.

Розрахунки тонкостінних стрижнів проводяться відносно головного полюса і головної нульової точки. Це точки, відносно котрих деякі секторіальні геометричні характеристики дорівнюють нулю.

Головний полюс збігається із центром кручення, тобто точкою, відносно якої відбувається поворот перерізу. Відносно головного полюса лінійно-секторіальні статичні моменти дорівнюють нулю. Для визначення головного полюса спочатку вибираємо довільно допоміжний полюс . Відстані та від допоміжного полюса до головного полюса визначаються так:

Д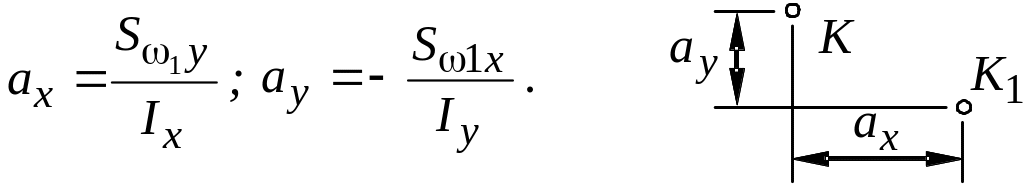 одатні значення та відкладаються в додатному напрямку головних осей.

Секторіальна координата головної нульової точки .

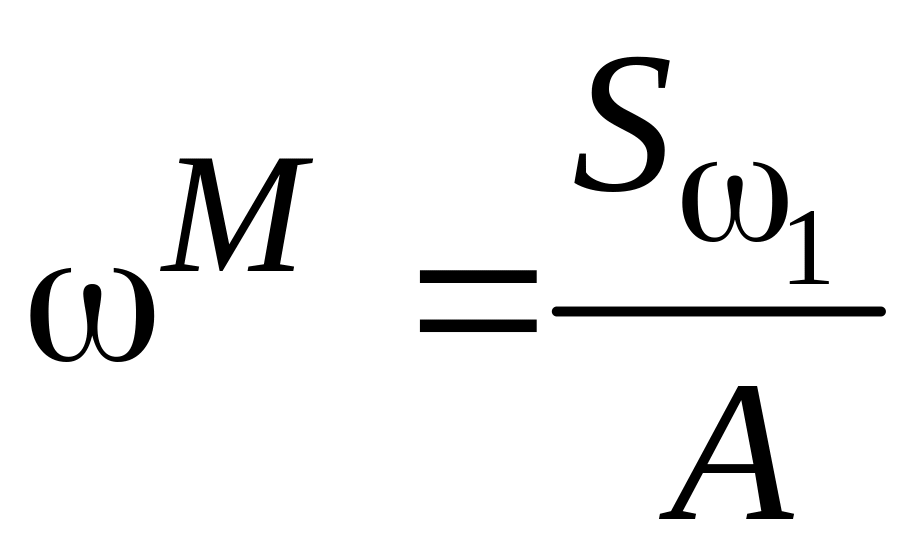Безпосередньо з аналізу умов рівності нулю секторіального та секторіально-лінійного статичних моментів можна зробити висновки:

1. Головна нульова точка знаходиться на перетині осі симетрії і середньої лінії профілю.

2. Головний полюс (центр кручення) повинен розміщуватися на осі симетрії.

3. У випадку, коли переріз складається із прямокутників, що перетинаються в одній точці, центр кручення розташовується в цій точці.

Напруження, які виникають при обмеженому крученні:

– секторіальні нормальні напруження від дії бімоменту .

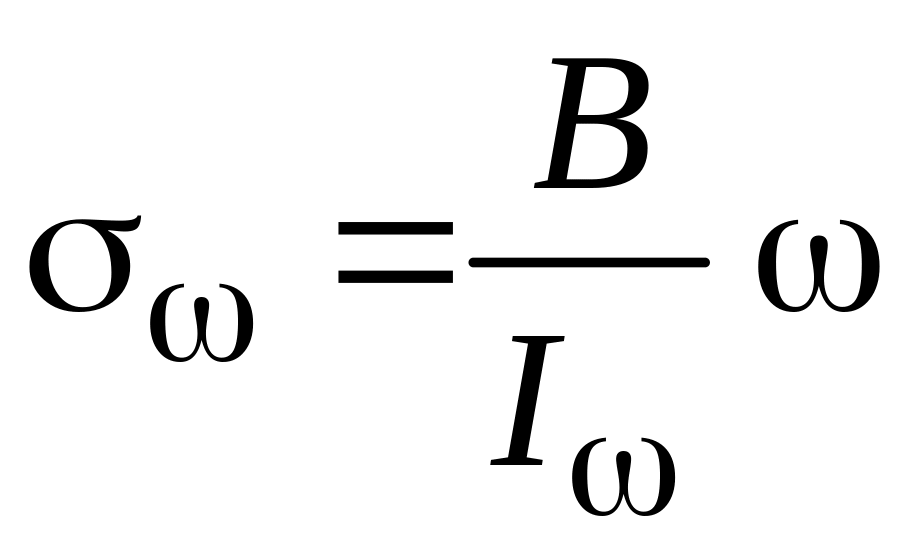Бімомент – система двох моментів, які розташовані в паралельних площинах та діють у протилежних напрямках;

– дотичні напруження вільного кручення від дії моменту чистого кручення

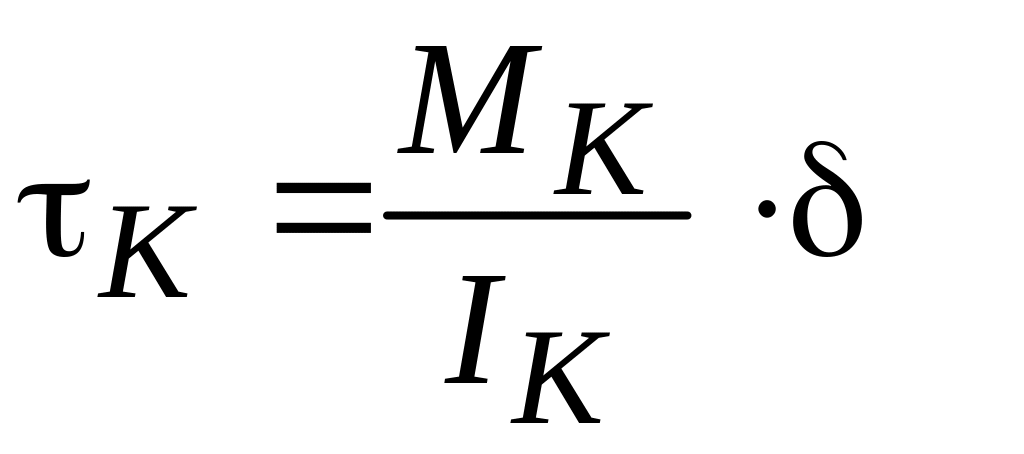, де ;

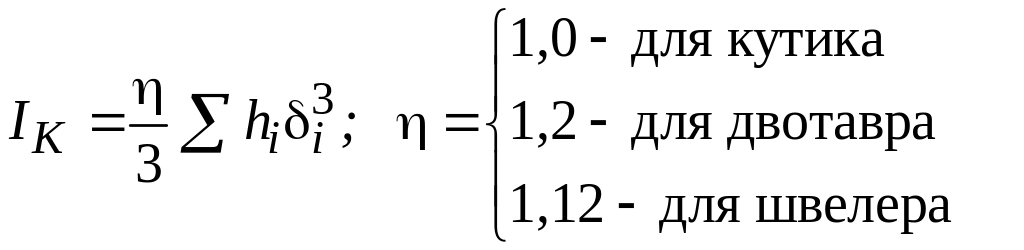– секторіальні дотичні напруження від дії згинно-крутного моменту

.
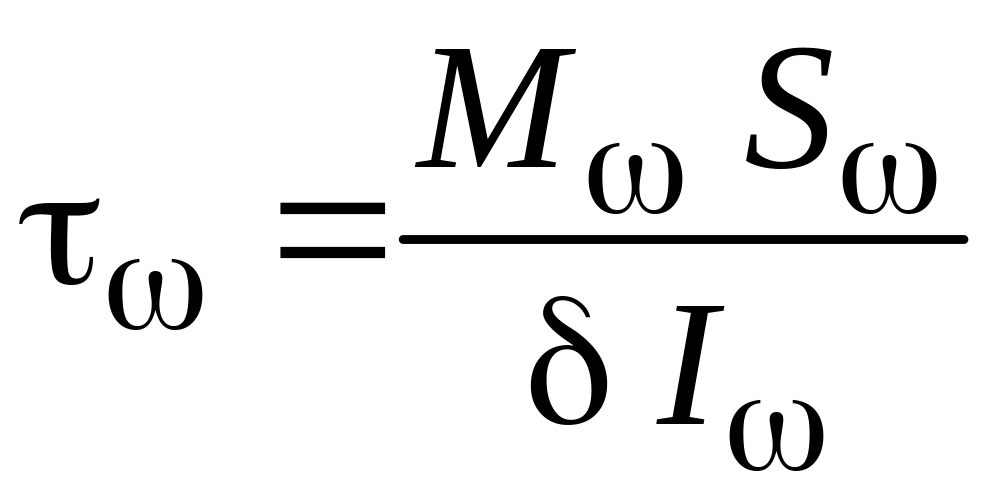