Мажорируемые ряды

Опр. Функциональный ряд называется мажорируемым в

области Х, если такой сходящийся знакоположительный числовой ряд

, что выполняются в каждой точке Х соотношения

.Соответствующий числовой ряд называется

мажорантным.

Замечание. Мажорируемый ряд – абсолютно сходящийся ряд.

Понятие о равномерной сходимости функционального ряда

Вопрос о том, при каких условиях сумма ряда – функция непрерывная, когда функциональный ряд можно почленно дифференцировать и интегрировать решается с помощью понятия равномерной сходимости ряда.

Опр. Функциональный ряд называется равномерно сходящимся на множестве Х, если для

.

Замечание. Геометрическая иллюстрация: у = S(х), у = S(х) – ε, у = S(х) + ε.

Для лежит в этой полосе.

Теорема. (Достаточный прзнак равномерной сходимости ряда, признак Вейерштрасса).

Мажорируемый ряд является рядом равномерно сходящимся.

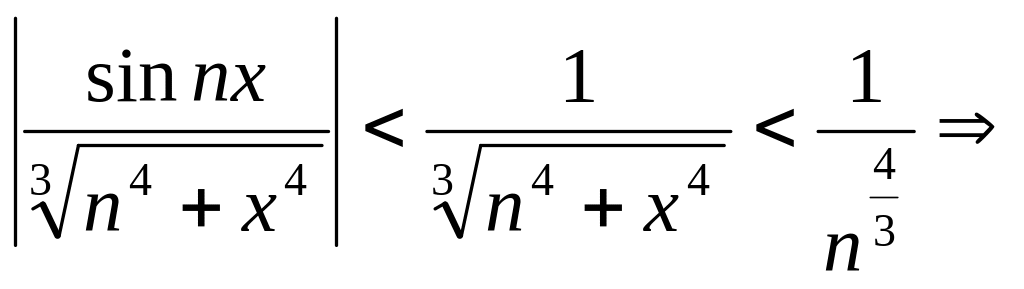Пример. Доказать, что ряд сходится равномерно на всей числовой оси.

ряд сходится равномерно на всей числовой оси.

Свойства равномерно сходящихся рядов

Теорема 1. Если ряд сходится равномерно на Х, на котором его члены

непрерывны, то сумма ряда S(x) непрерывна на этом множестве.

Теорема 2. Если функции непрерывны на Х и ряд сходится равномерно на Х, то ряд,

полученный интегрированием членов данного ряда также сходится равномерно

на Х, причем

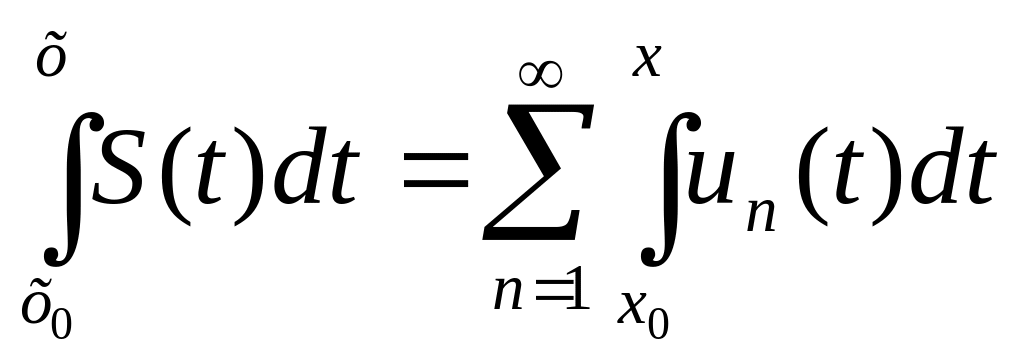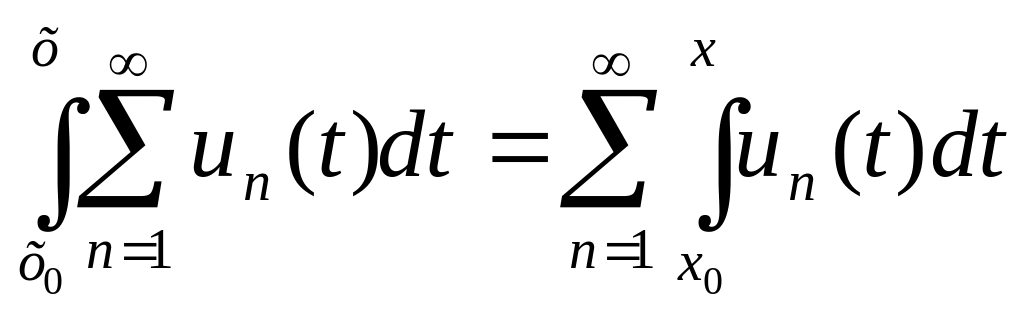или , где .

Теорема 3. Пусть функции определены на множестве Х и имеют на нем непрерывные производные . Если на этом множестве сходится ряд и равномерно сходится ряд, составленный из производных , то сумма S(x) ряда имеет производную, равную сумме ряда , т.е.

или .

Степенные ряды

Степенные ряды – это простейшие функциональные ряды.

Опр. Степенным рядом называется ряд вида

(1) - степенной ряд

по степеням (х –с) . а_n – числа, коэффициенты ряда,с– число.

В простейшем случае с = 0, тогда ряд (1) приобретает вид

(2) – степенной ряд по степеням х.

Очевидно, что путем подстановки от первого ряда можно перейти ко второму, поэтому теорию степенных рядов рассматривают для ряда(2).

Теорема Абеля. Если степенной ряд (2) сходится при , то он абсолютно

сходится для любого х, удовлетворяющего условию . Если при

, ряд (2) расходится, то он расходится для любого х,

удовлетворяющего условию .

Следствие. Для каждого степенного ряда (2) существует число R > 0, называемое

радиусом сходимости этого ряда и обладающее следующими свойствами:

при ряд (2) сходится абсолютно,

при ряд (2) расходится .

Промежуток (-R,R) называется интервалом сходимости степенного ряда(2). На

концах интервала вопрос о сходимости ряда решается индивидуально для

каждого конкретного ряда.

Способы определения радиуса сходимости: 1) по признаку Даламбера, 2) по радикальному признаку Коши.