Числовые ряды Числовая последовательность

Опр. Числовой последовательностью называют числовую ф-цию ,

определенную на множестве натуральных чисел.

х_n - общий член последовательности.

х_n = n² , х₁ = 1, х₂ = 4,…, х₁₀ =100,…

Опр. Если - последовательность называется сходящейся. Если

предел не существует, либо он равен , то последовательность называется

расходящейся.

Понятие числового ряда и его сходимости

Опр. Пусть задана числовая последовательность . Сумма элементов бесконечной

числовой последовательности называется числовым рядом.

Числа называются членами ряда, n-ый член ряда называется общим членом ряда.

Опр. Если все члены ряда а_n > 0(положительны), то ряд называется знакоположительным.

Опр. Сумма первых n слагаемых ряда называется n – частичной суммой ряда:

.

Опр. Если предел n – частичной суммы ряда существует и конечен, то ряд называется

сходящимся, в противном случае (предел n – частичной суммы ряда не существует

или равен бесконечности) говорят, что ряд расходится.

. Этот предел называется суммой числового ряда.

,

,

,

.

Опр. Остатком ряда после n-го члена (или n-м остатком) R_n называют ряд, полученный из данного путем отбрасывания его n первых членов .

Тогда сумма ряда может быть записана выражением . Так как сумма S_n первых n членов ряда всегда конечное число, то сходимость ряда определяется сходимостью его остатка R_n=S – S_n.

Свойства сходящихся числовых рядов

1. Ряд и его остаток либо одновременно сходятся, либо расходятся. Остаток сходящегося ряда стремится к нулю: .

2. Сходящиеся ряды можно почленно складывать, вычитать, умножать все члены сходящегося ряда на постоянное числдо, перемножать ряды как два многочлена, и при этом полученные ряды будут являться сходящимися, т.е если , ,

то , , .

Необходимое условие сходимости числового ряда

Теорема. Если числовой ряд сходится , тогда предел его общего члена равен 0:

.

Приведенный признак сходимости следует понимать так:

Если , то ряд расходится точно,

если , то ряд может сходиться, но может и расходиться.

Пример. Исследовать на сходимость ряды:

1. , ряд расходится.

2. , ряд расходится.

3. , ряд расходится.

4. , ряд расходится.

5. , ряд может как сходиться, так и расходиться.

Таблица эквивалентных величин

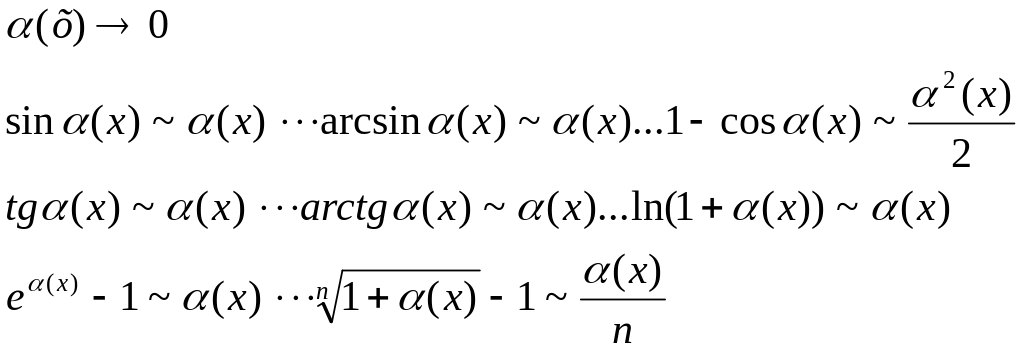
- многочлен степени n.

При ,

при .

Пример. Выполняется ли необходимый признак сходимости ряда?

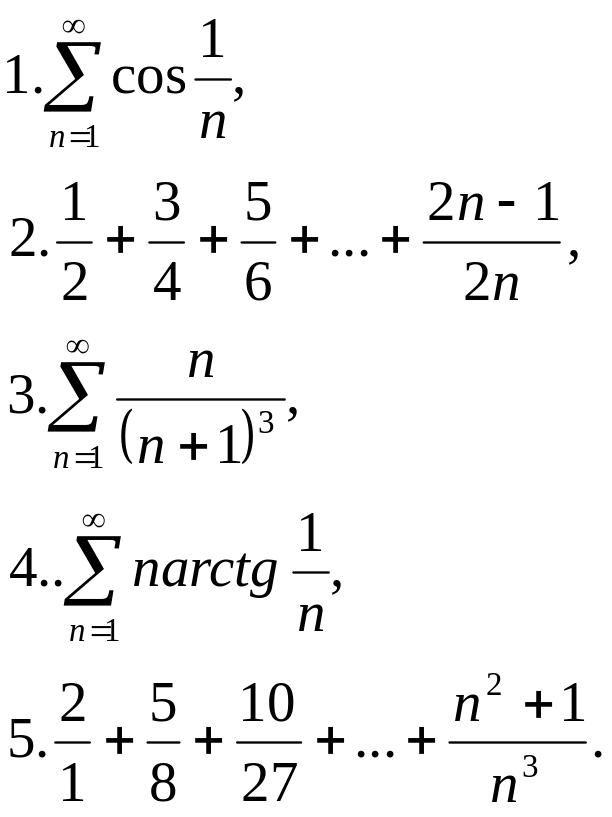
Факт расходимости ряда при выполнении необходимого признака сходимости говорит о том, что для сходимости ряда кроме убывания и стремления к нулю общего члена ряда нужна достаточная скорость убывания ряда, чтобы сумма бесконечного числа членов не успела накапливаться.

Прежде, чем вычислять сумму ряда необходимо убедиться, что он сходится. Достаточные признаки сходимости числовых рядов дают ответ на эти вопросы.