§ 5. Ортогональные системы векторов.

Векторное пространство , в котором скалярное произведение векторов и определяется формулой , является евклидовым.

Два вектора и называются ортогональными, если .

Система векторов называется ортогональной, если векторы этой системы попарно ортогональны: при .

Базис -мерного евклидова пространства называется ортогональным, если при .

Каждый вектор единственным образом раскладывается по базису : , где числа называемые координатами вектора в ортогональном базисе , определяются по формулам: ( ).

Ортогональной составляющей вектора относительно ортогональной системы векторов называется вектор , где ( ).

Процессом ортогонализации системы векторов называется построение ортогональной системы ненулевых векторов по формулам: , , ,…, , где - ортогональные составляющие векторов относительно ортогональных систем векторов ( ). Если система векторов линейно зависима, то число векторов в ортогональной системе будет меньше .

1.123 Выяснить будут ли ортогональными следующие системы векторов.

а) ;

б) ;

в) ;

г) .

1.124 Проверить ортогональность систем векторов и дополнить их до ортогональных базисов.

а) ;

б) ;

в) ;

г) .

1.125 Найти координаты вектора в ортогональном базисе: , , , .

1.126 Найти координаты вектора в ортогональном базисе: , , .

1.127 Найти ортогональную составляющую вектора относительно ортогональной системы векторов .

а) ;

б) ;

в) ;

г) .

В задачах 1.128-1.133 применяя процесс ортогонализации построить ортогональную систему векторов.

1.128 .

1.129 .

1.130 .

1.131 .

1.132 .

1.133 .

§ 6. Линейные операторы.

Оператором в (преобразованием пространства ) называется закон, по которому каждому вектору ставится в соответствие единственный вектор , и пишут Оператор называется линейным, если для любых векторов и действительных чисел выполнено условие: .

Если - базис , то матрицей линейного оператора в базисе называется квадратная матрица порядка , столбцами которой являются столбцы координат векторов . Каноническим базисом называется базис , где , , -единичные векторы. Между линейными операторами, действующими в и квадратными матрицами порядка , существует взаимно однозначное соответствие, что позволяет оператор представлять в матричном виде , где - матрицы-столбцы координат векторов , - матрица оператора в базисе .

Для линейных операторов вводятся операции: 1) сложение операторов: ; 2) умножение оператора на число: ; 3) умножение операторов: .

Обратным к оператору называется оператор такой, что , где - единичный (тождественный) оператор, реализующий отображение . Обратный оператор существует только для невырожденных операторов (операторов, матрица которых является невырожденной). Все, рассмотренные выше, действия над линейными операторами выполняют, выполняя аналогичные действия над их матрицами.

Пусть число и вектор , , таковы, что выполняются равенства: или . Тогда число называется собственным числом линейного оператора (матрицы ), а вектор - собственным вектором оператора (матрицы), соответствующим собственному числу . Равенство может быть записано и в виде , где - единичная матрица порядка , - матрица-столбец координат собственного вектора , соответствующего собственному числу , - нулевая матрица-столбец.

Характеристическим уравнением оператора (матрицы ) называется уравнение: .

Множество собственных чисел оператора (матрицы) совпадает с множеством корней его характеристического уравнения: , а множество собственных векторов, отвечающих собственному числу , совпадает с множеством ненулевых решений матричного уравнения: .

Если квадратная матрица порядка имеет собственные числа кратности , где , то она приводима к диагональному виду тогда и только тогда, когда выполнены условия: ( ). Если нарушается хотя бы одно из условий, то матрица к диагональному виду неприводима.

Приведение матрицы к диагональному виду осуществляется преобразованием: , где - матрица, столбцами которой являются линейно независимых собственных векторов матрицы , отвечающих собственным числам (каждому собственному числу кратности отвечает линейно независимых собственных векторов, образующих фундаментальную систему решений уравнения: ). Матрица при этом будет иметь диагональный вид, причём на главной диагонали будут стоять собственные числа матрицы .

В задачах 1.134-1.138 установить, какие из заданных отображений пространства арифметических векторов в себя являются линейными операторами, и выписать их матрицы в каноническом базисе.

1.134 .

1.135 .

1.136 .

1.137 .

1.138 .

В задачах 1.139-1.143 в пространстве заданы линейные операторы и . Найти матрицу линейного оператора , где и его явный вид в каноническом базисе .

1.139 ,

.

1.140 ,

.

1.141 ,

.

1.142 ,

.

1.143 .

.

В задачах 1.144-1.146 установить, какие из заданных в линейных операторов являются невырожденными, и найти явный вид обратных операторов .

1.144 .

1.145 .

1.146 .

В задачах 1.147-1.156 найти собственные числа и собственные векторы линейных операторов,заданных своими матрицами

1.147 . 1.148 .

1.149 . 1.150 .

1.151 . 1.152 .

1.153 . 1.154 .

1.155 . 1.156 .

В задачах 1.157-1.166 выяснить, какие из заданных матриц линейных операторов можно диагонализировать и найти:

а) диагональную форму матрицы; б) матрицу линейного преобразования, приводящего данную матрицу к диагональному виду.

1.157 . 1.158 .

1.159 . 1.160 .

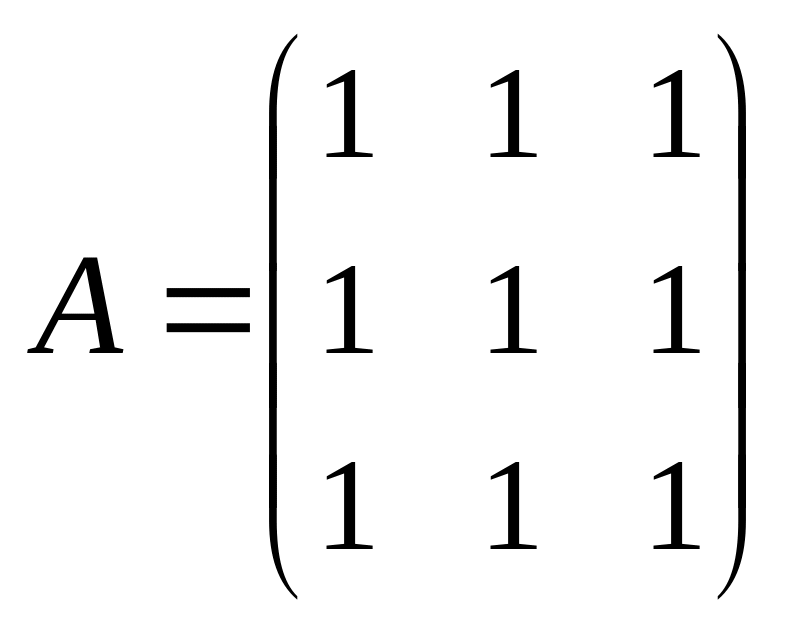1.161 . 1.162 .

1.163 . 1.164 .

1.165 . 1.166 .