
- •Глава 1. Линейная алгебра.
- •§ 1. Определители.
- •§ 2. Матрицы.
- •§3. Пространство арифметических векторов. Ранг матрицы.
- •§4. Системы линейных уравнений.
- •§ 5. Ортогональные системы векторов.
- •§ 6. Линейные операторы.
- •§ 7. Квадратичные формы.
- •§ 8. Системы линейных уравнений и неравенств.
- •Глава 2. Векторная алгебра.
- •§1. Линейные операции над векторами.
Глава 1. Линейная алгебра.
§ 1. Определители.
Квадратной
матрицей порядка
![]() называется квадратная таблица из чисел
называется квадратная таблица из чисел
![]() (
(![]() ,
,
![]() ):
):
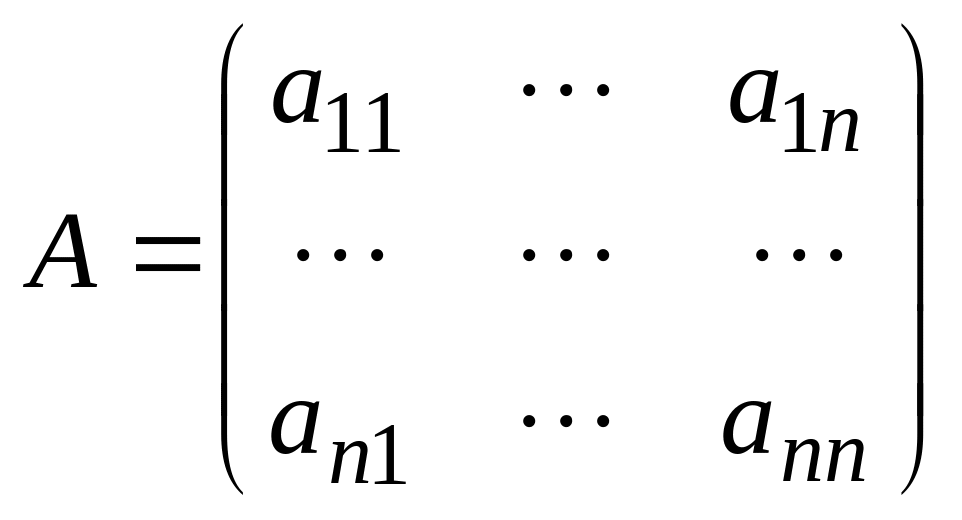 ,
состоящая из
,
состоящая из
![]() строк и
столбцов. Любой квадратной матрице
строк и
столбцов. Любой квадратной матрице
![]() порядка
можно поставить в соответствие число
порядка
можно поставить в соответствие число![]() ,
равное алгебраической сумме
,
равное алгебраической сумме
![]() слагаемых, составленных определённым
образом из элементов
слагаемых, составленных определённым
образом из элементов
![]() матрицы
матрицы
![]() ,
называемое определителем матрицы.
,
называемое определителем матрицы.
Определителем
1-ого порядка
называется число
![]() .
.
Определителем 2-ого порядка называется число
![]() .
.
Определителем 3-его порядка называется число
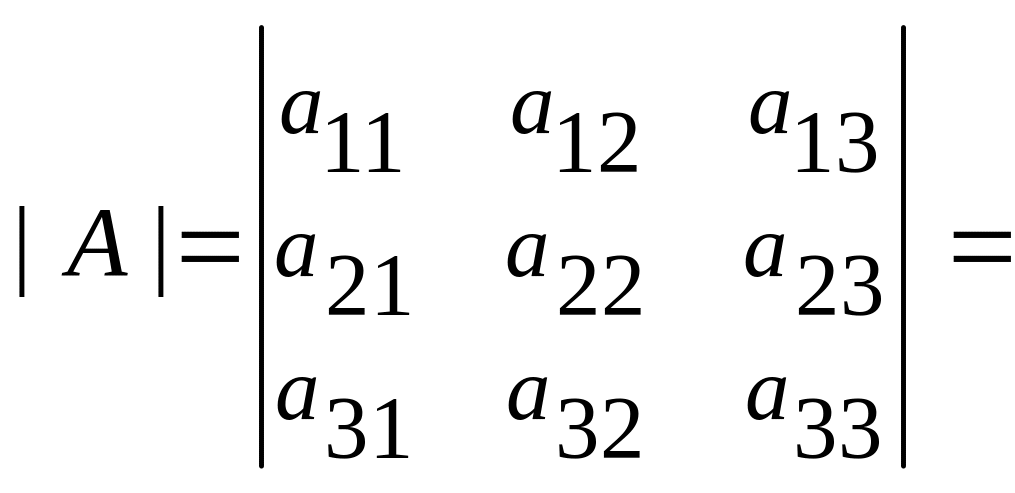
![]()
Минором элемента
![]() определителя
называется определитель
определителя
называется определитель![]() ,
полученный из данного вычёркиванием
,
полученный из данного вычёркиванием
![]() -ой
и
-ой
и
![]() -ого
столбца. Алгебраическим
дополнением
-ого
столбца. Алгебраическим
дополнением
![]() элемента
называется его минор
,
взятый со знаком
элемента
называется его минор
,
взятый со знаком
![]() :
:
![]() .
.
Определителем порядка называется число
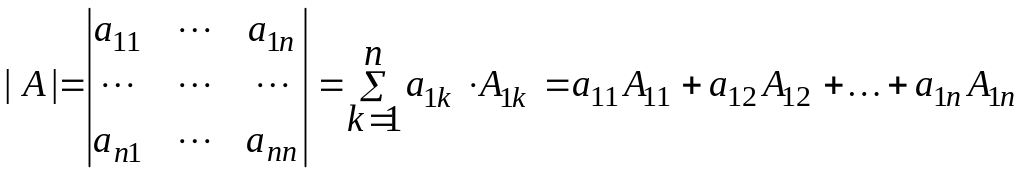
Разложением
определителя
по
![]() -ой
строке (
)
называется соотношение:
-ой
строке (
)
называется соотношение:
![]() .
.
Разложением
определителя![]() по
по![]() -ому
столбцу (
)
называется соотношение:
-ому
столбцу (
)
называется соотношение:
![]()
Определители обладают свойствами:
1) определитель не изменится при замене всех его строк столбцами с теми же номерами;
2) определитель изменит знак на противоположный, если переставить местами любые две строки (два столбца) определителя;
3) общий множитель элементов какой-либо строки (столбца) можно вынести за знак определителя;
4) определитель равен нулю, если он содержит нулевую строку (столбец), две одинаковые или пропорциональные строки (столбца);
5) определитель не изменится, если к какой-либо строке (столбцу) прибавить другую строку (столбец), умноженную на любое число;
6) определитель треугольного вида (когда все элементы, лежащие по одну сторону одной из его диагоналей равны нулю) равен произведению диагональных элементов.
В задачах 1.1-1.4 вычислить определители 2-го порядка.
1.1
![]() .
1.2
.
1.2
![]() .
1.3
.
1.3
![]() .
1.4
.
1.4
![]() .
.
В задачах 1.5-1.8 вычислить определители 3-го порядка.
1.5
 .
1.6
.
1.6
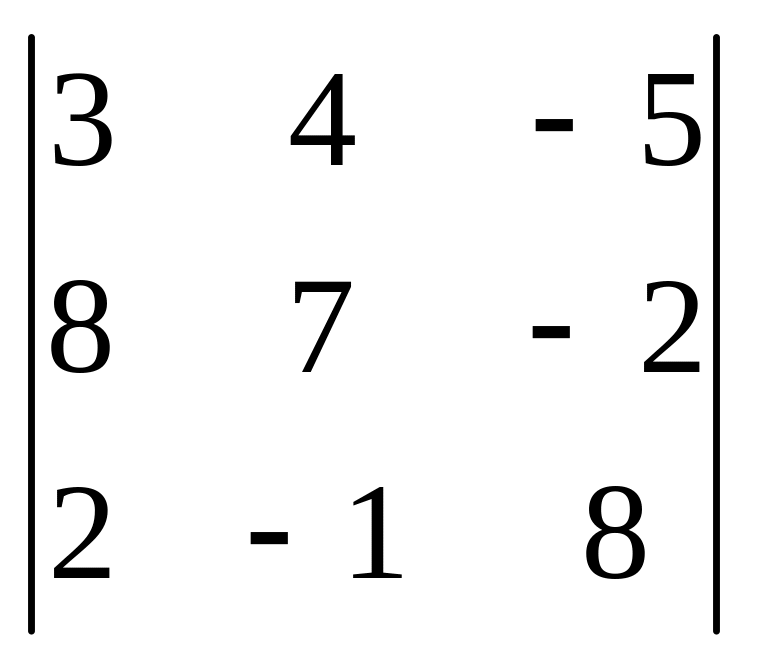 .
1.7
.
1.7
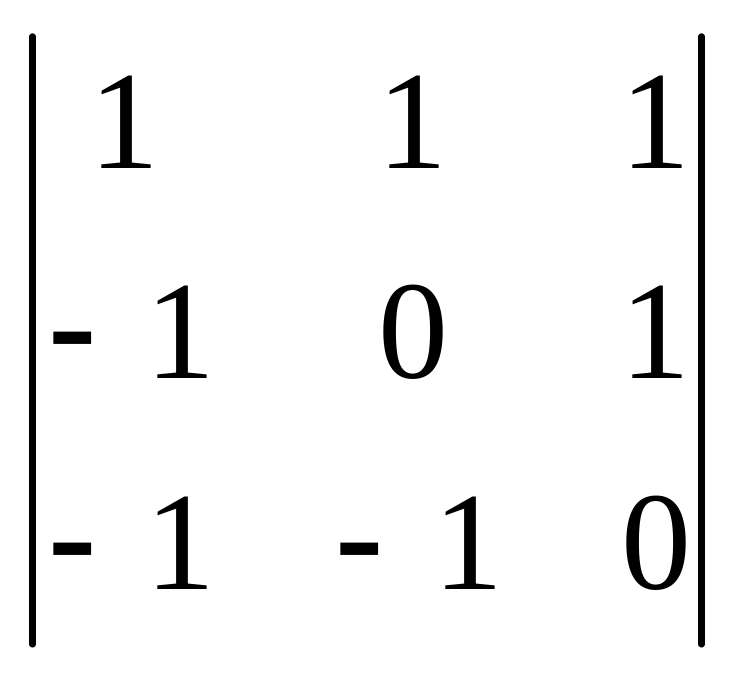 .
1.8
.
1.8
 .
.
1.9 Решить уравнение.
а)
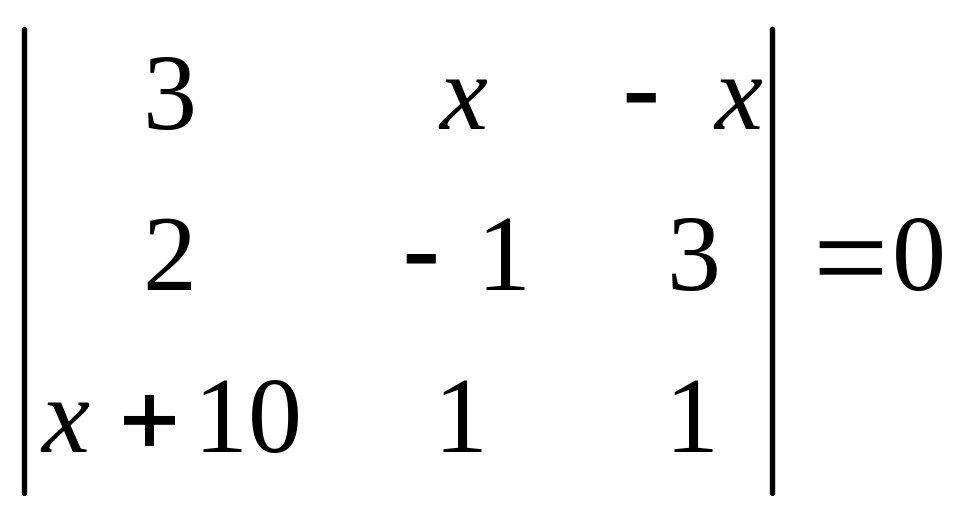 ;
б)
;
б)
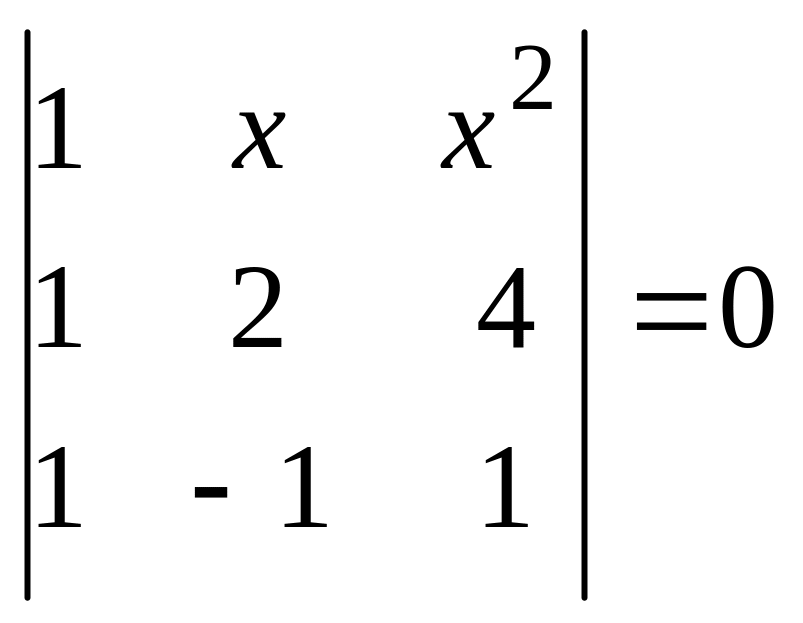 ;
в)
;
в)
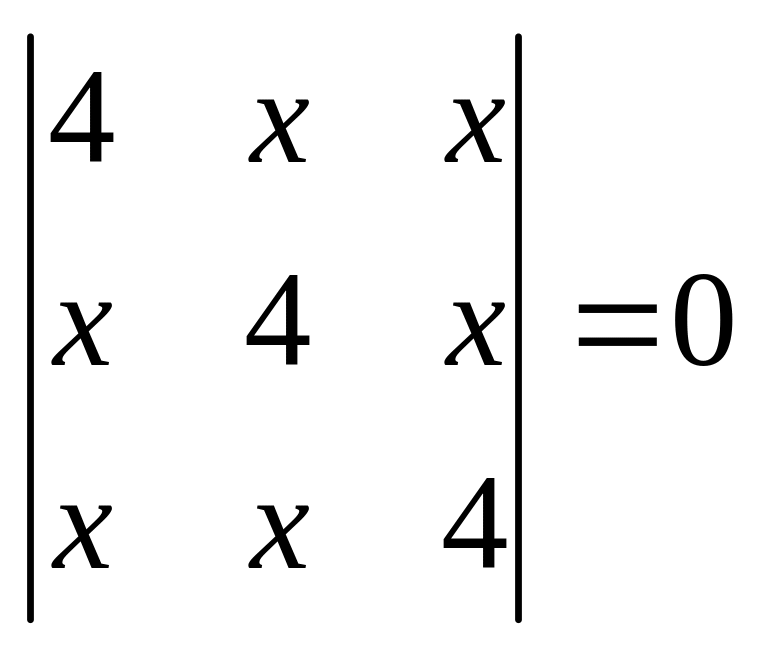 .
.
1.10
Решить неравенство.![]()
а)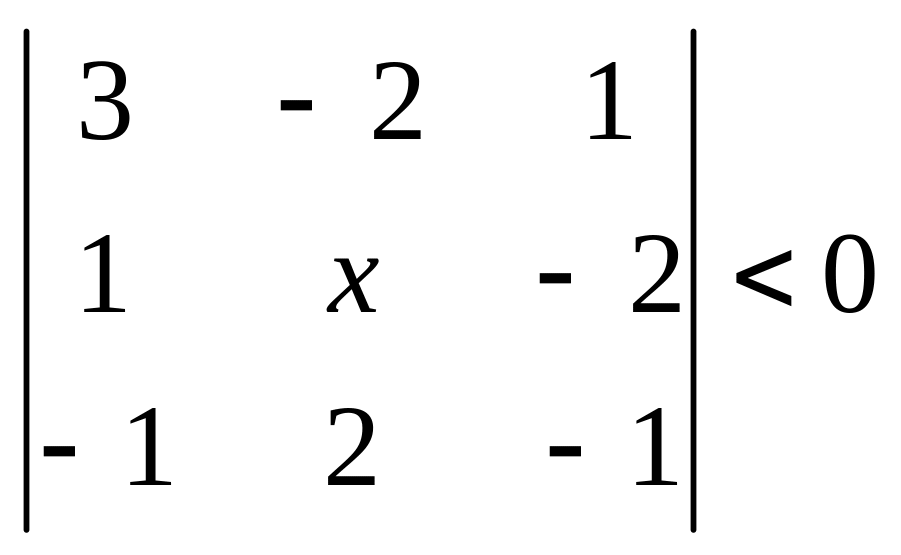 ;
б)
;
б)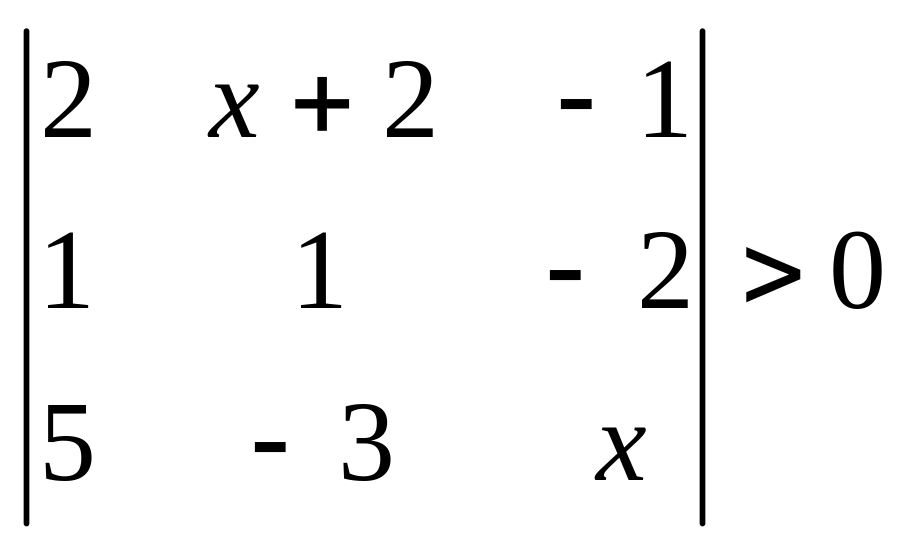 ;
в)
;
в)
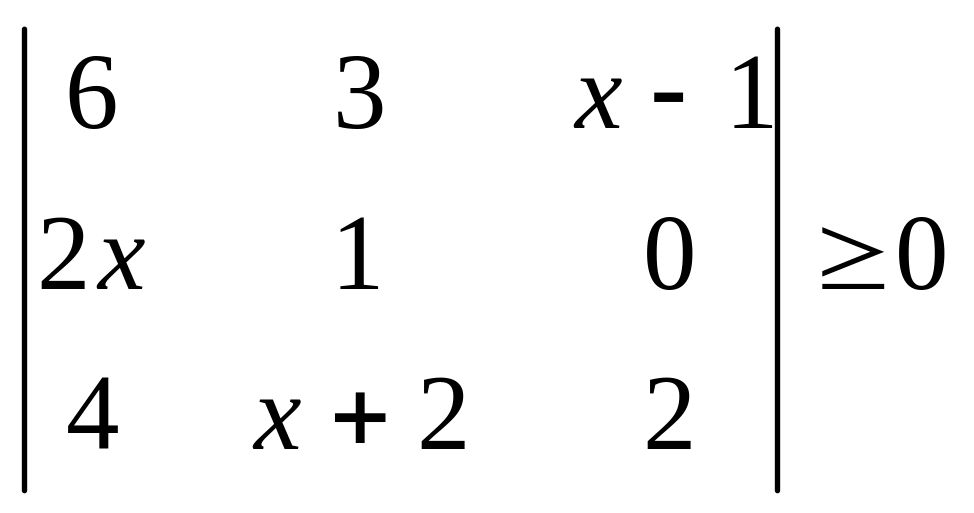 .
.
В задачах 1.11-1.12, используя свойства определителя, доказать тождества (определители не развертывать).
1.11
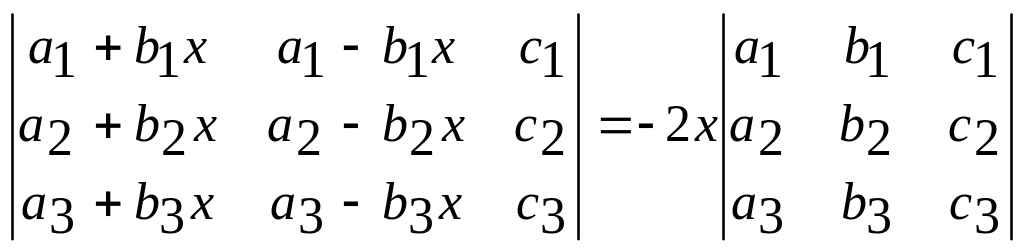 .
.
1.12
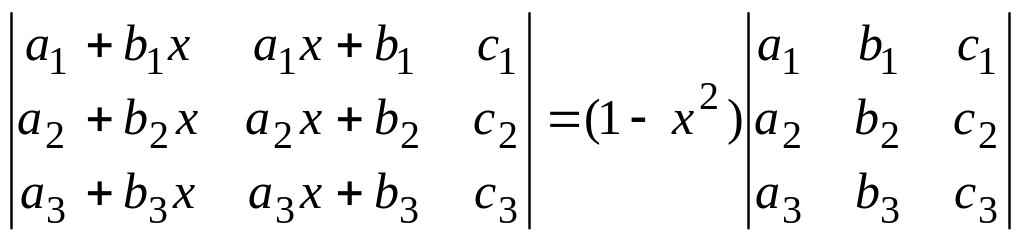 .
.
В задачах 1.13-1.16 вычислить определители, используя их свойства
1.13
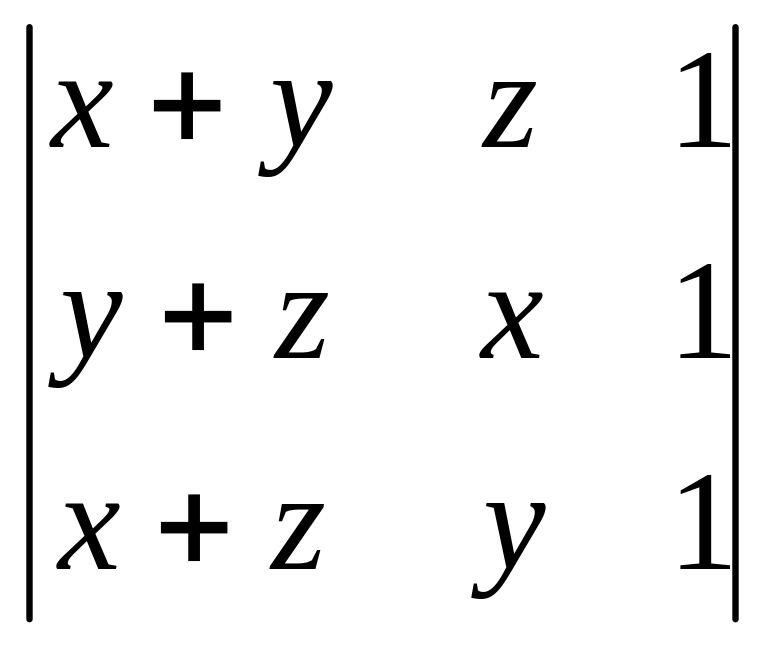 .
1.14
.
1.14
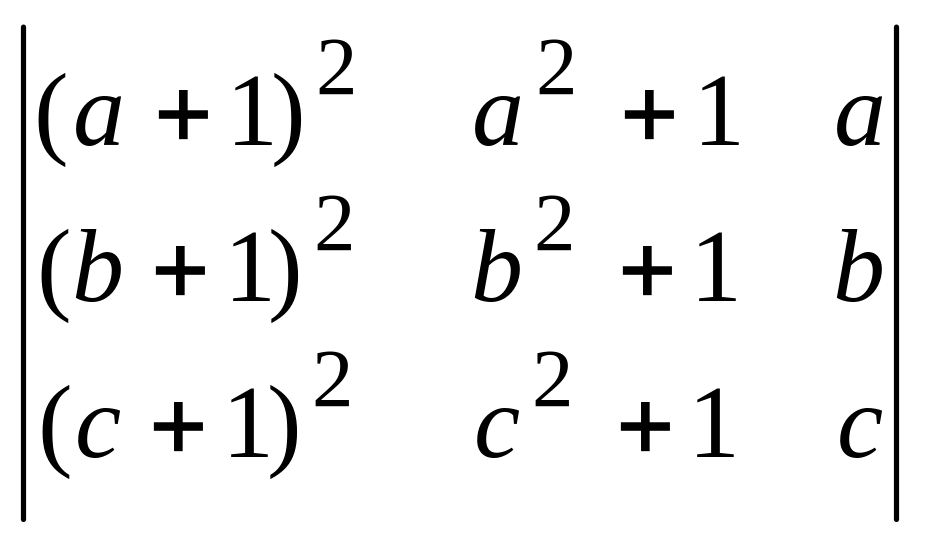 .
.
1.15
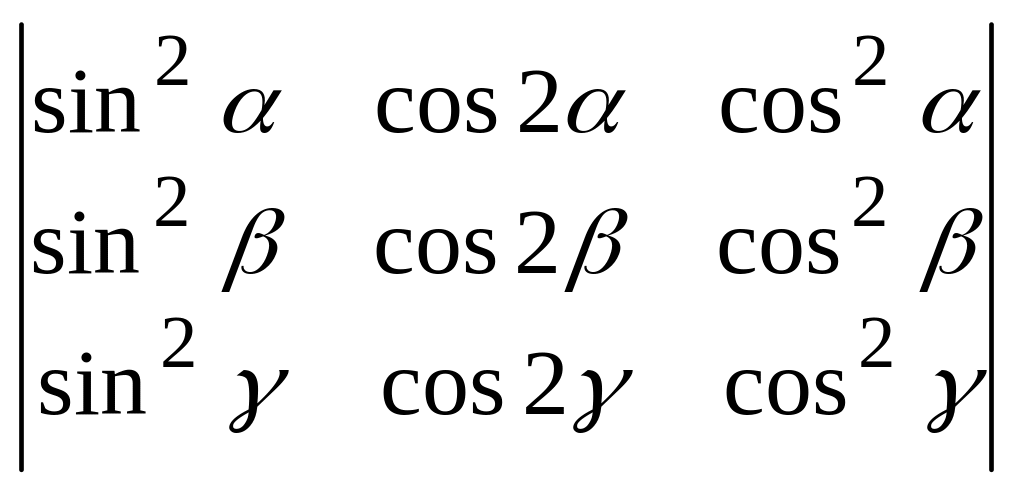 .
1.16
.
1.16
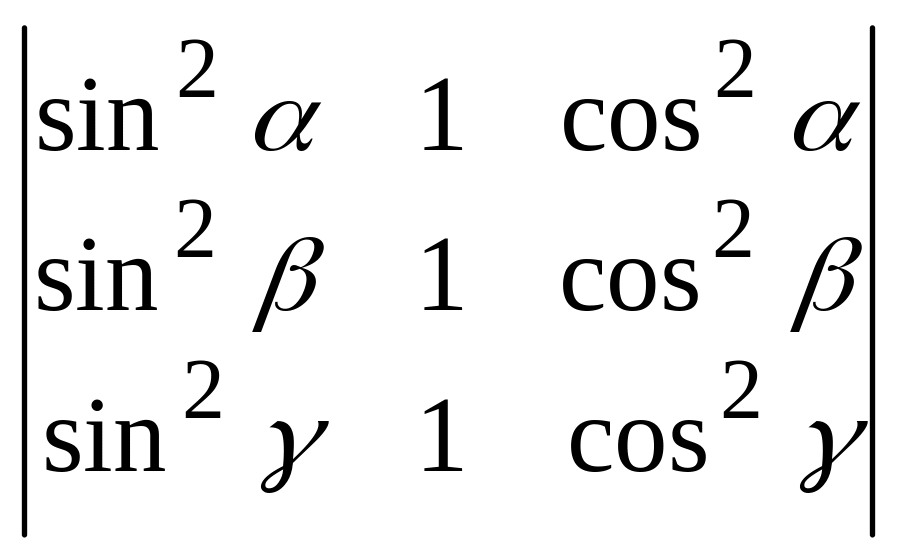 .
.
1.17 Проверить,
что определитель
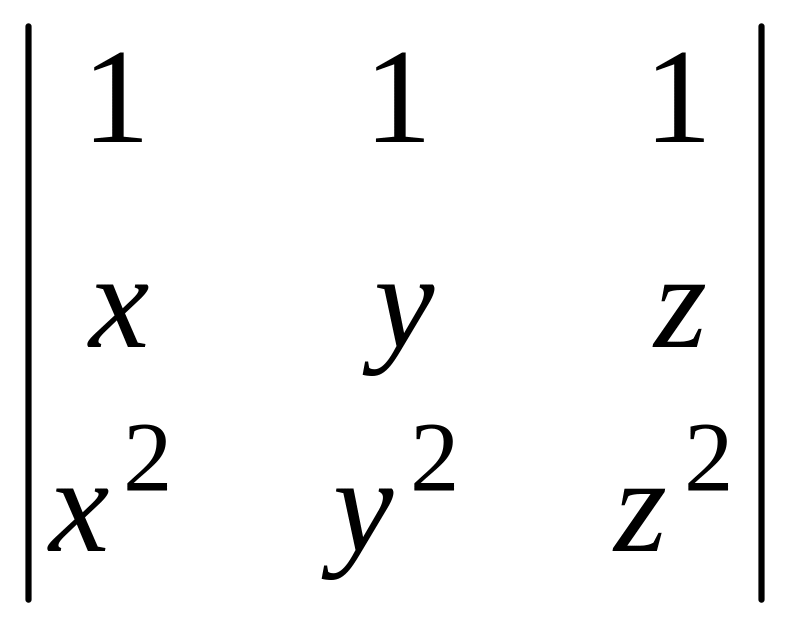 делится на
делится на
![]() и
и
![]()
В задачах 1.18-1.23 вычислить определители, используя разложение по строке или столбцу:
1.18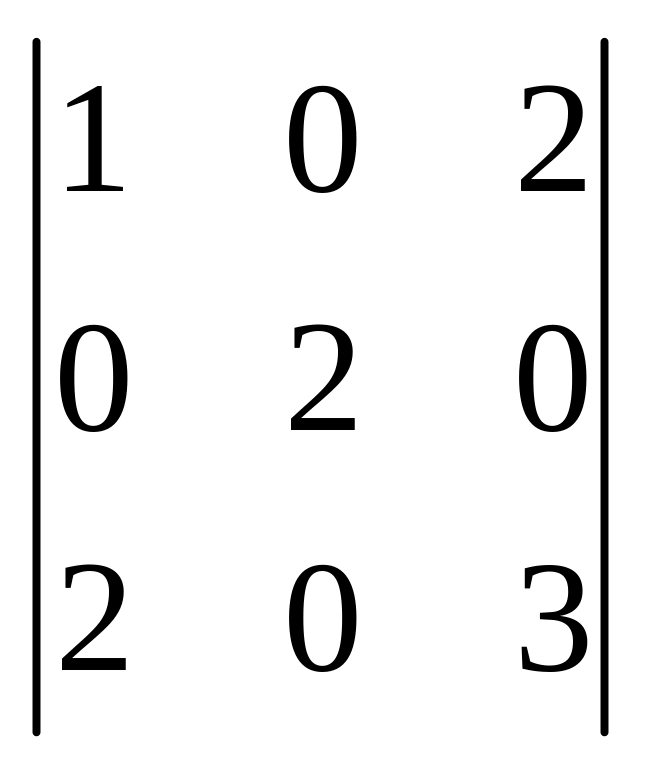 .
1.19
.
1.19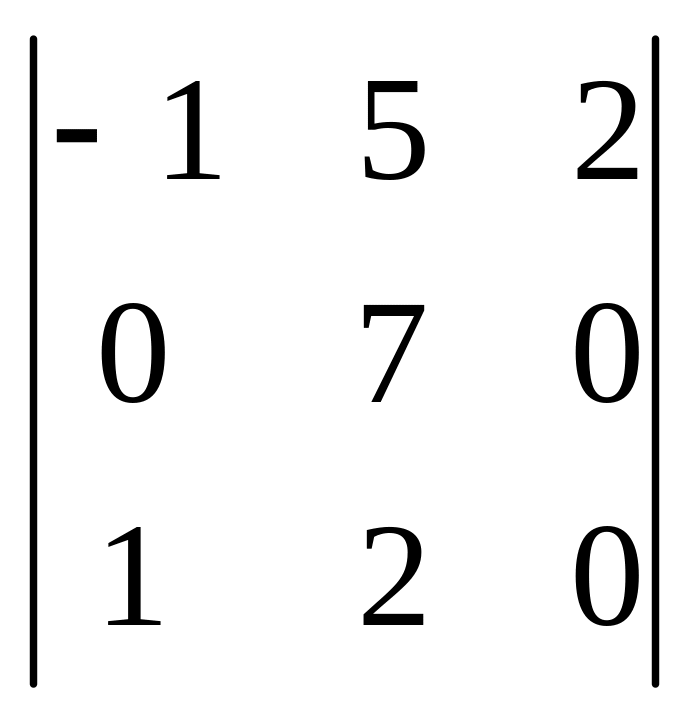 .
1.20
.
1.20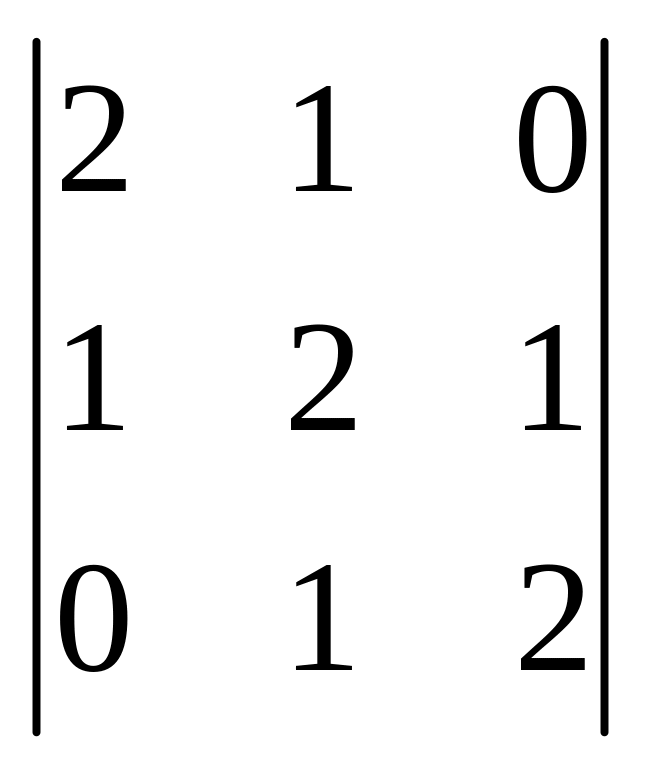 .
1.21
.
1.21
 .
.
1.22
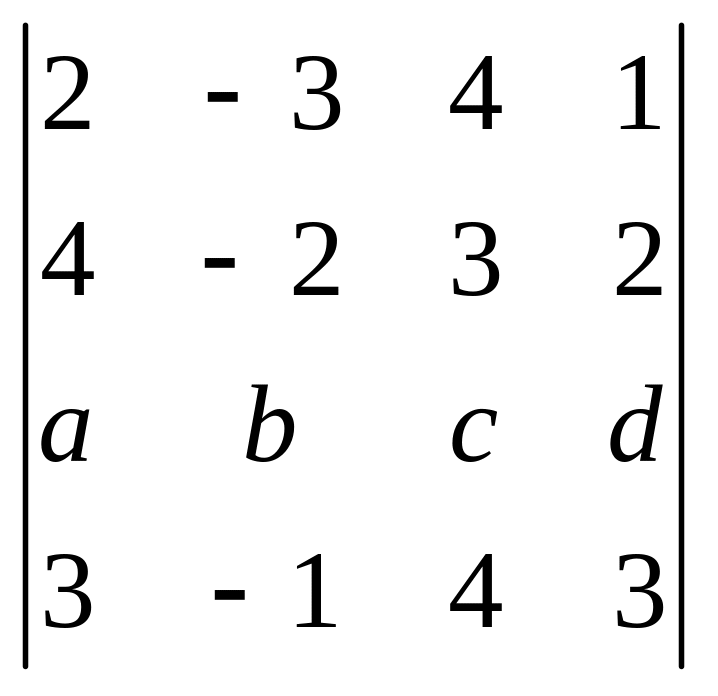 .
1.23
.
1.23
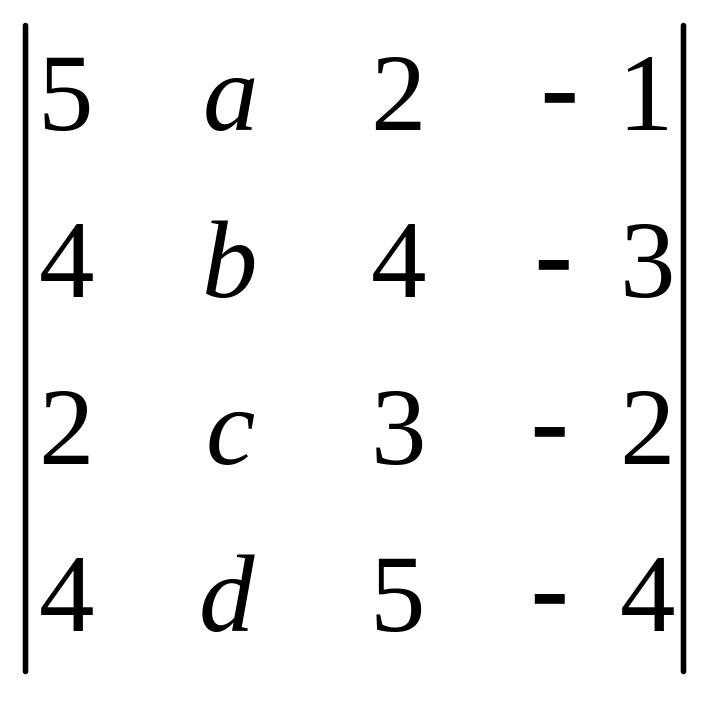 .
.
В задачах 1.24-1.29 вычислить определители
1.24
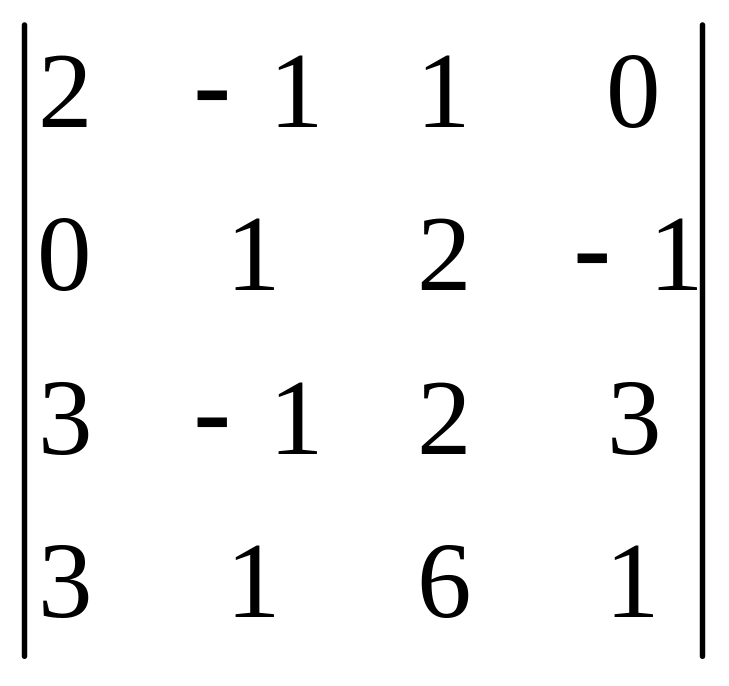 .
1.25
.
1.25
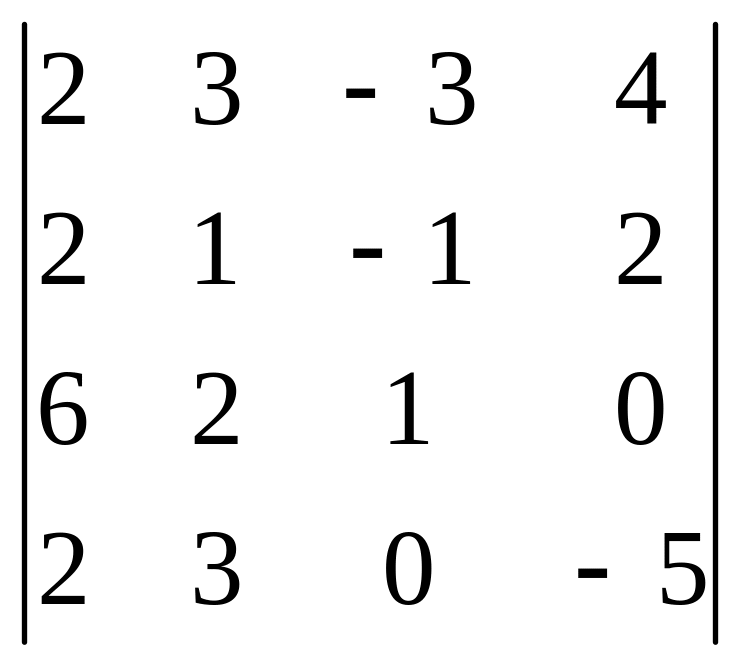 .
1.26
.
1.26
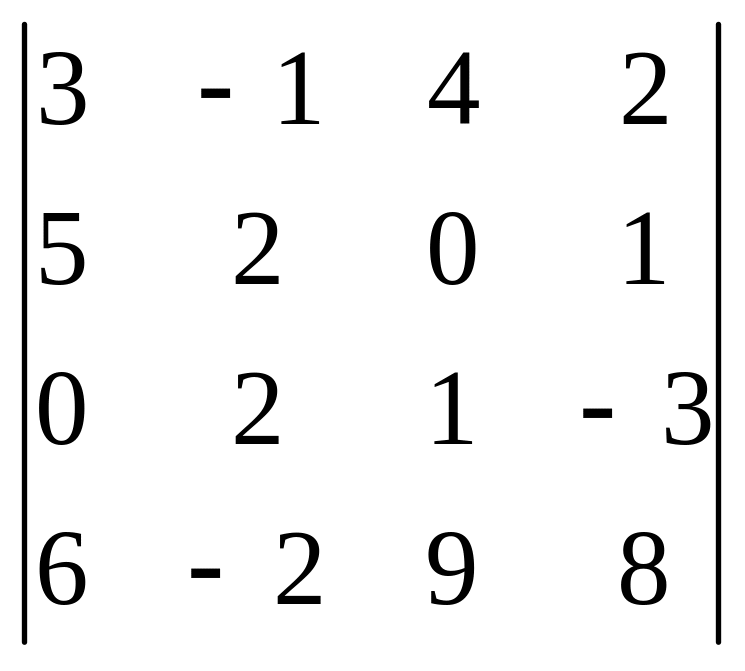 .
.
1.27
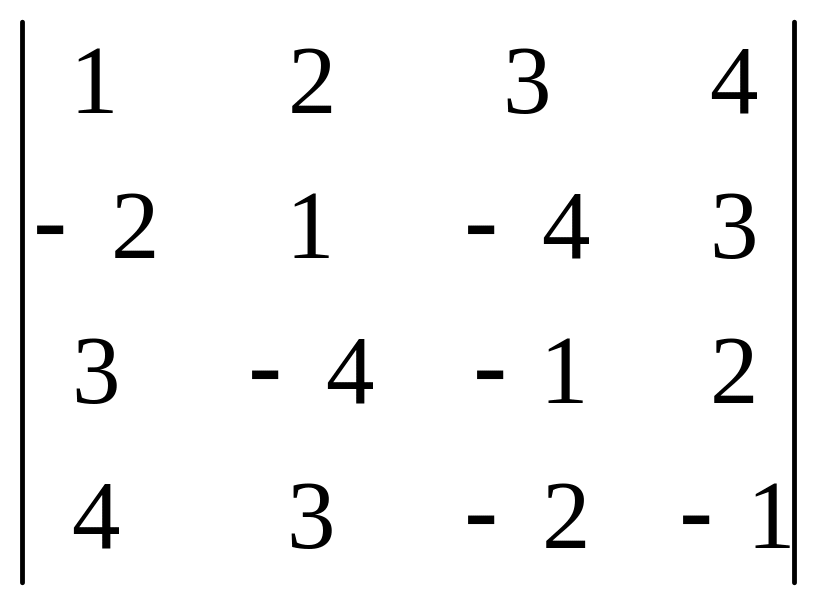 .
1.28
.
1.28
 .
1.29
.
1.29
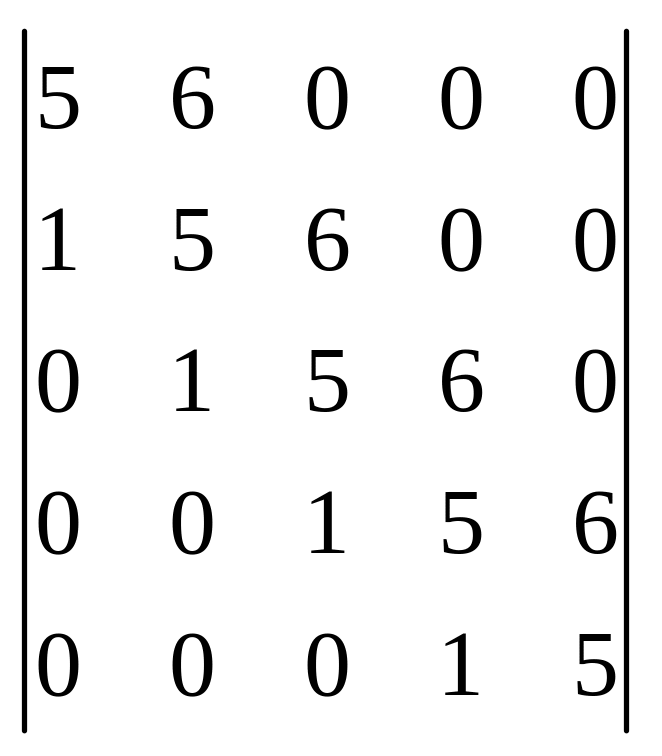 .
.
§ 2. Матрицы.
Матрицей размера
![]() называется
прямоугольная таблица из чисел
(
называется
прямоугольная таблица из чисел
(![]() ,
,
![]() ):
):
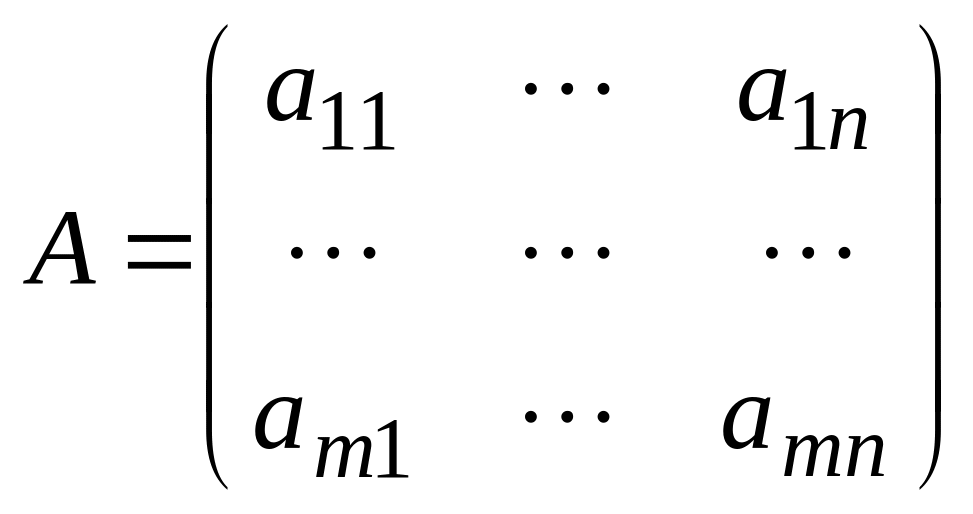 ,
состоящая из
,
состоящая из
![]() строк и
столбцов. Если необходимо указать её
размер, то пишут
строк и
столбцов. Если необходимо указать её
размер, то пишут
![]() .
.
Матрицы
и
![]() называются равными
и
пишут
называются равными
и
пишут
![]() ,
если они одинакового размера и их
соответствующие элементы равны:
,
если они одинакового размера и их
соответствующие элементы равны:
![]() ,
,![]() ,
.
,
.
Транспонированной
к матрице
![]() называется матрица
называется матрица
![]() ,
столбцами которой являются соответствующие
строки матрицы
,
столбцами которой являются соответствующие
строки матрицы
![]() .
.
Суммой (разностью)
матриц
и
одного размера
![]() ,
называется матрица
,
называется матрица
![]() того же размера, для которой:
того же размера, для которой:
![]() ,
,
.
,
,
.
Произведением
матрицы
на число
![]() называется матрица
называется матрица
![]() того же размера, для которой:
того же размера, для которой:
![]() ,
,
.
,
,
.
Линейной
комбинацией
матриц
и
одного размера
,
называется матрица
![]() того же размера (
и
того же размера (
и
![]() - произвольные числа), для которой:
- произвольные числа), для которой:
![]() ,
,
,
,
,
,
Произведением
матрицы
![]() на матрицу
на матрицу
![]() называется матрица
называется матрица
![]() ,
каждый элемент которой
,
каждый элемент которой
![]() вычисляется по правилу:
вычисляется по правилу:
![]() ,
,
,
,
![]() .
.
Вообще говоря,
![]() .
.
Элементарными преобразованиями матрицы называются:
1) перестановка строк (столбцов);
2) умножение строки (столбца) на число, отличное от нуля;
3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число;
4) вычёркивание нулевой строки (столбца).
Матрицы и , полученные одна из другой в результате элементарных преобразований называются эквивалентными и пишут ~ .
Обратной
к квадратной матрице
называется матрица
![]() того же порядка такая, что:
того же порядка такая, что:
![]() ,
где
,
где
![]() - единичная матрица (на главной диагонали
которой стоят единицы, а все остальные
элементы равны нулю). Обратная матрица
всегда существует для невырожденных
матриц. Квадратная матрица
называется невырожденной,
если её определитель
- единичная матрица (на главной диагонали
которой стоят единицы, а все остальные
элементы равны нулю). Обратная матрица
всегда существует для невырожденных
матриц. Квадратная матрица
называется невырожденной,
если её определитель
![]() .
.
Основными методами вычисления обратной матрицы являются:
Метод присоединённой
матрицы.
Если
-невырожденная
матрица, то
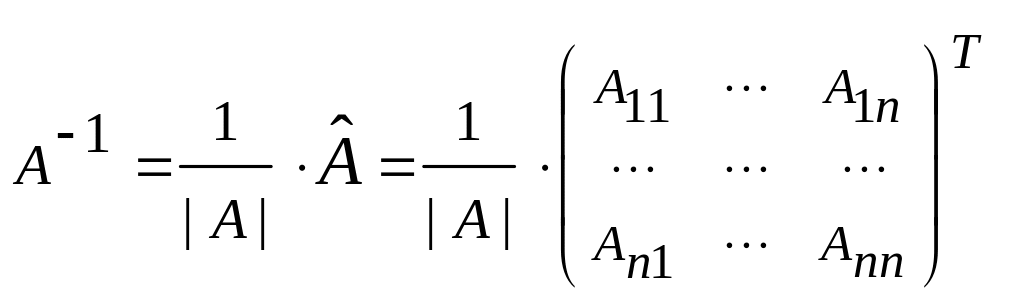 ,
где
,
где
![]() - присоединённая матрица, для которой:
- присоединённая матрица, для которой:
![]()
![]() .
Здесь
.
Здесь
![]() - алгебраические дополнения элементов
- алгебраические дополнения элементов
![]() матрицы
.
матрицы
.
Метод элементарных
преобразований. Для
матрицы
порядка
строится прямоугольная матрица
![]() размера
размера
![]() приписыванием к
справа единичной матрицы. Далее, с
помощью элементарных преобразований
над строками, матрица
приводится к виду
приписыванием к
справа единичной матрицы. Далее, с
помощью элементарных преобразований
над строками, матрица
приводится к виду![]() ,
что всегда возможно, если
-невырожденная.
,
что всегда возможно, если
-невырожденная.
Матричными
называются
уравнения:![]() ,
,
![]() ,
,
![]() ,
где матрицы
,
где матрицы![]() - известны, матрица
- известны, матрица
![]() -
неизвестна. Если матрицы
,
-невырожденные, то решения матричных
уравнений записываются, соответственно,
в виде:
-
неизвестна. Если матрицы
,
-невырожденные, то решения матричных
уравнений записываются, соответственно,
в виде:
![]() ,
,![]() ,
,![]() .
.
В задачах 1.30-1.31 найти линейные комбинации матриц:
1.30
![]() .
.
1.31
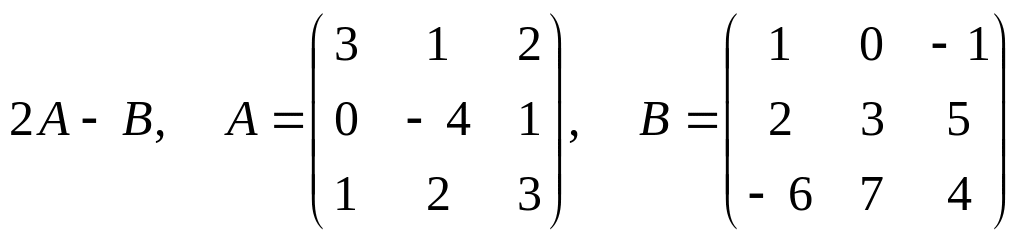 .
.
В задачах 1.32-1.35 умножить матрицы:
1.32 а)
![]() ;
б)
;
б)
![]() .
.
1.33 а)
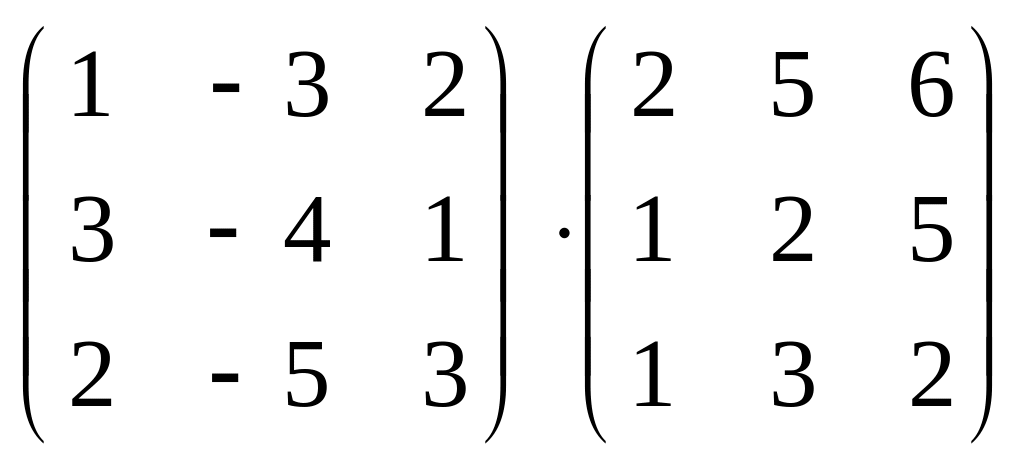 ;
б)
;
б)
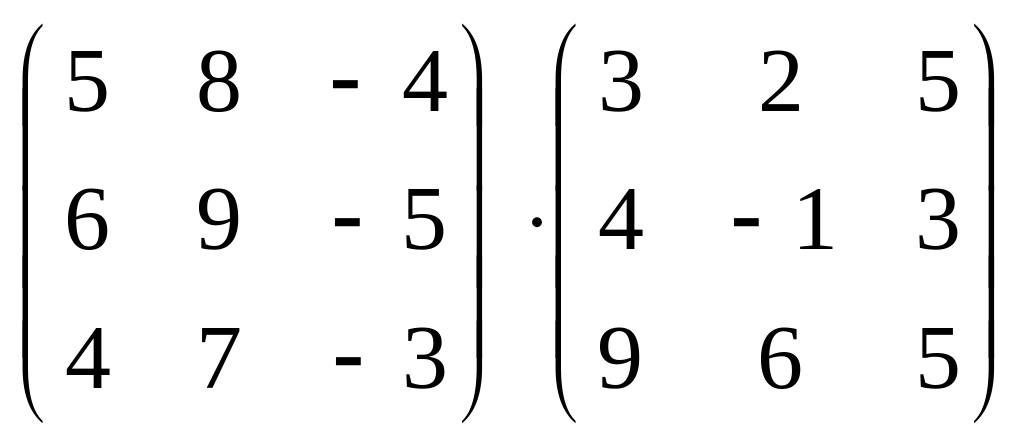 .
.
1.34 а)
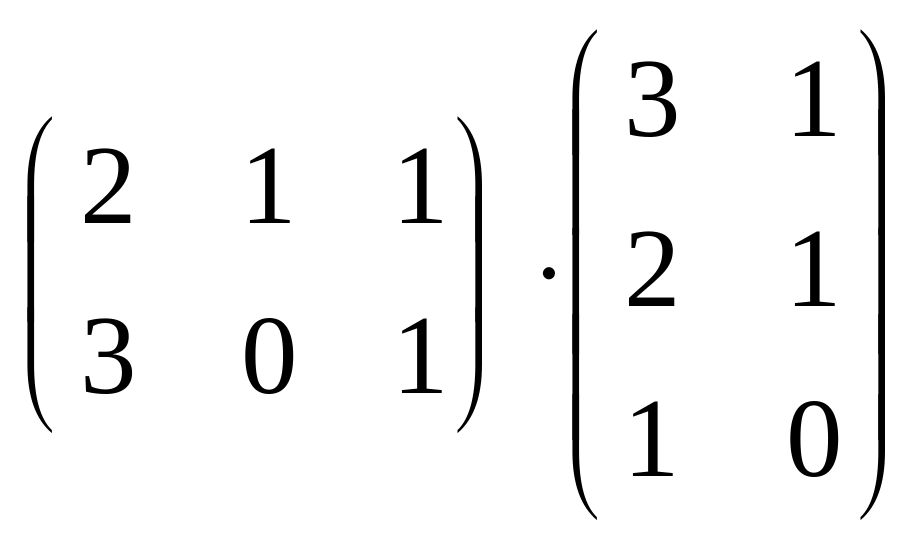 ;
б)
;
б)
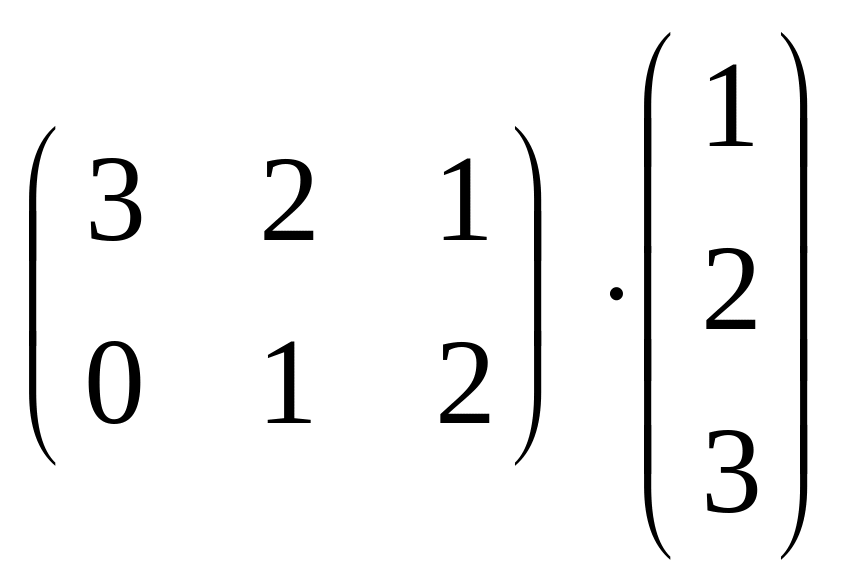 ;
;
в)
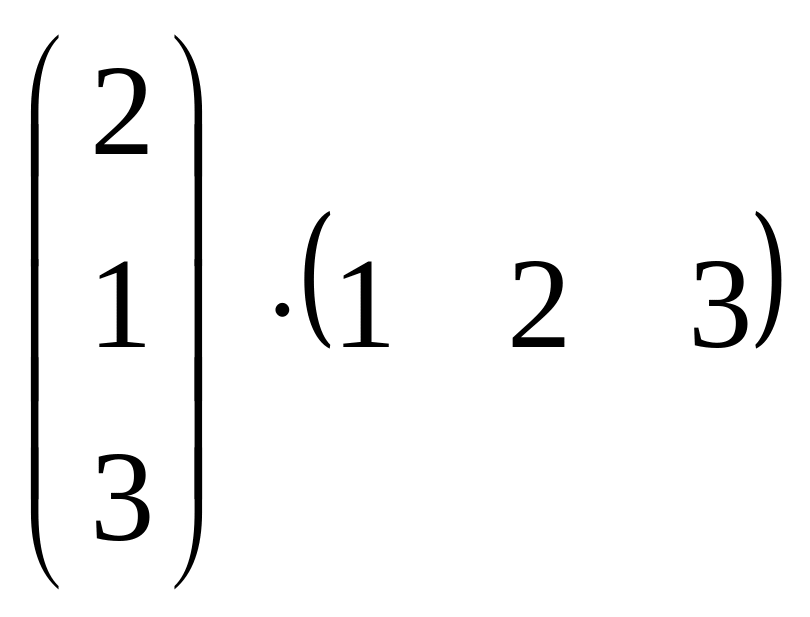 ;
г)
;
г)
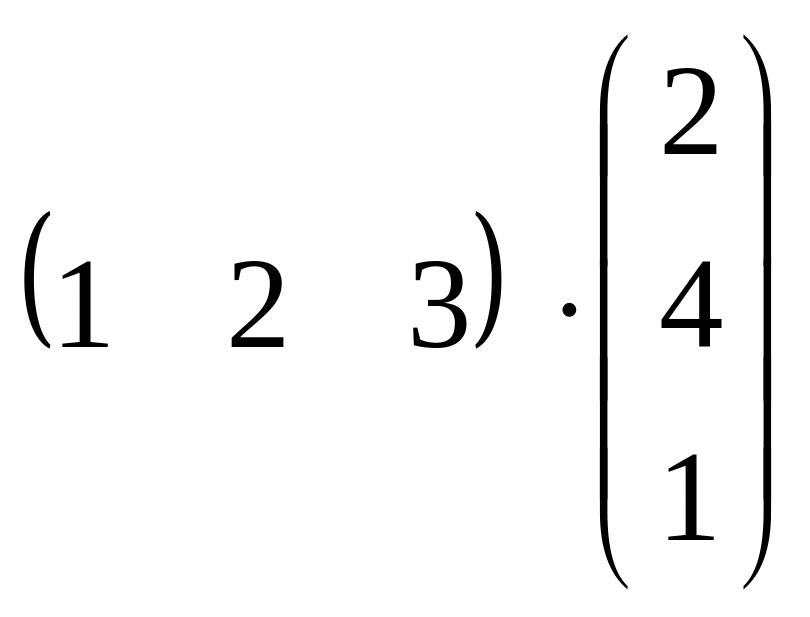 .
.
1.35 а)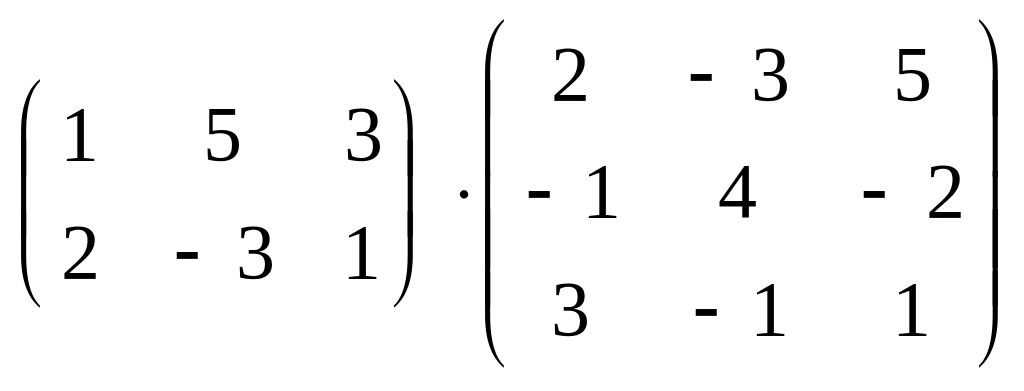 ;
б)
;
б)
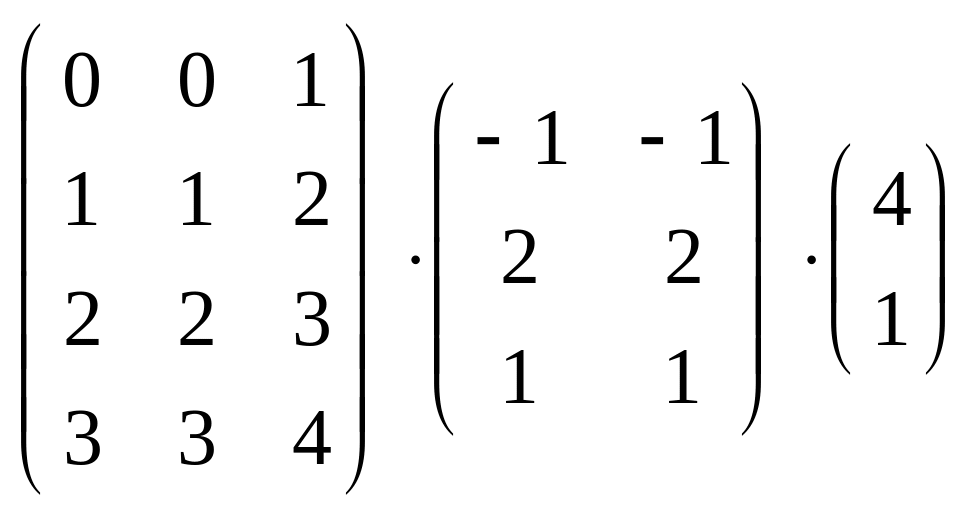 .
.
1.36 Выполнить действия над матрицами
а)
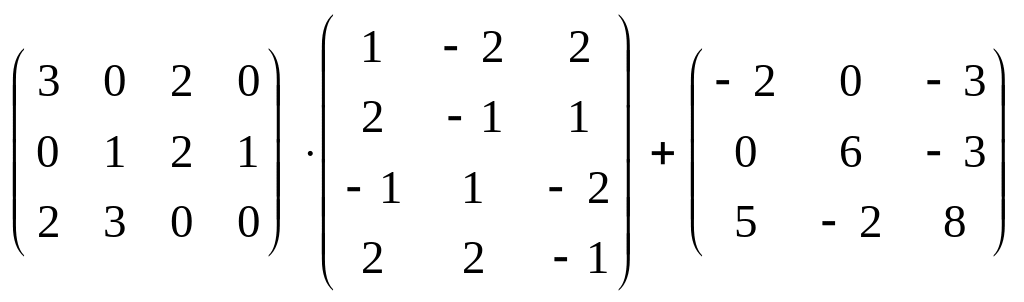 ;
;
б)
 .
.
1.37
Вычислить
а)
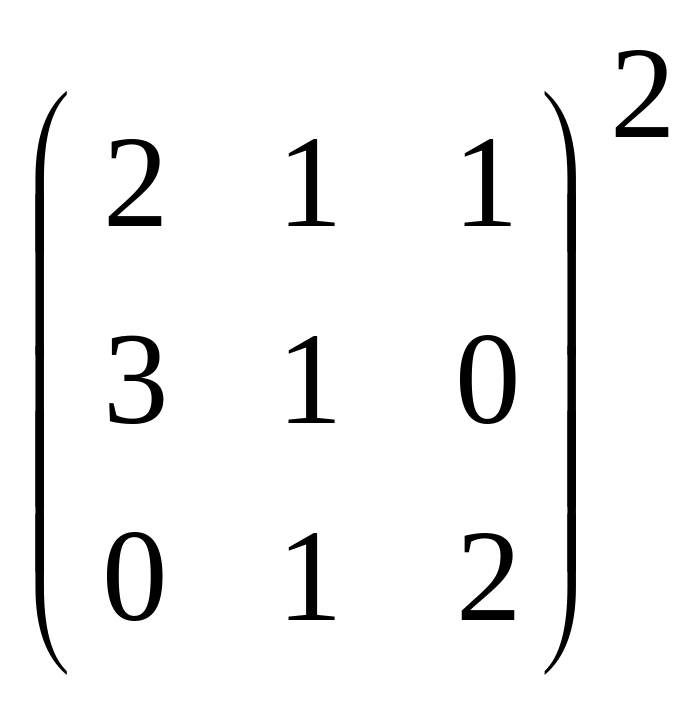 ;
б)
;
б)
![]() .
.
В задачах
1.38-1.40 найти
значение многочлена
![]() от матрицы
от матрицы
1.38![]() ,
,
![]() .
.
1.39![]() ,
,
![]() .
.
1.40
![]() ,
,
![]() .
.
В задачах
1.41-1.42 вычислить
![]() .
.
1.41
![]() ,
,
![]() .
.
1.42
![]() ,
,
![]() .
.
В задачах
1.43-1.44 вычислить
![]() для заданных матриц
для заданных матриц
![]() .
.
1.43
![]() .
1.44
.
1.44
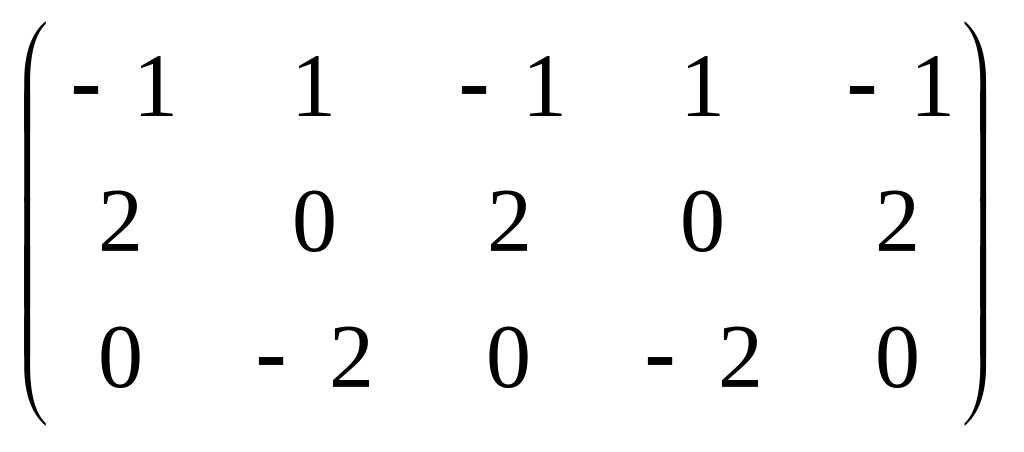 .
.
В задачах 1.45-1.52 найти обратную матрицу для матриц:
1.45
![]() .
1.46
.
1.46
![]() .
1.47
.
1.47
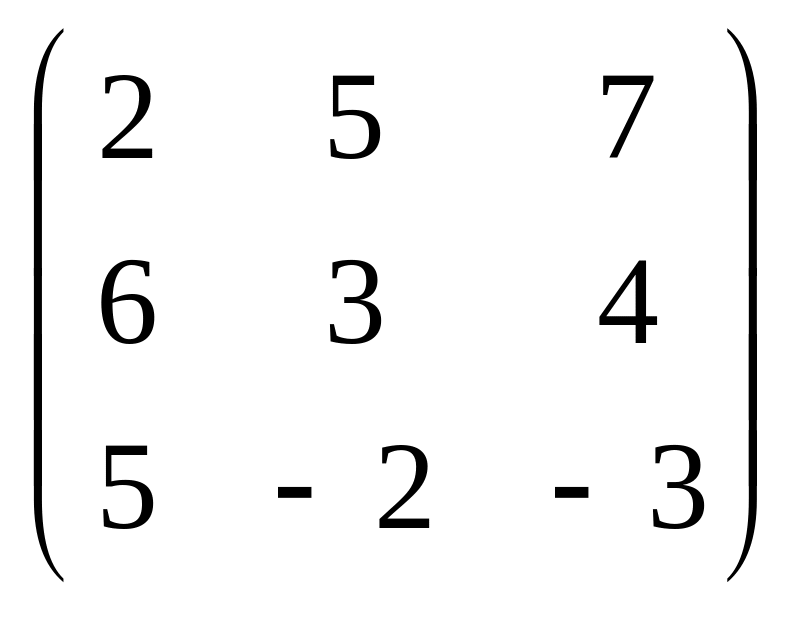 .
.
1.48
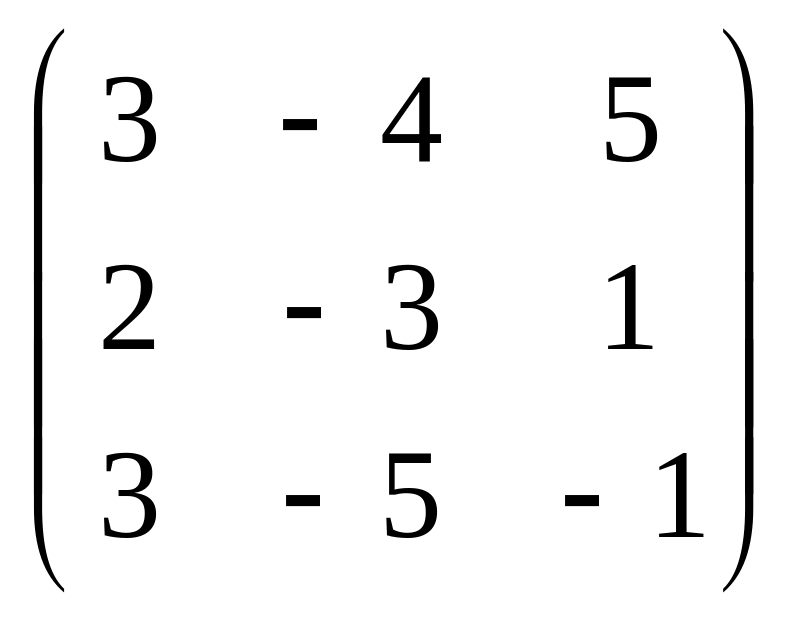 .
1.49
.
1.49
 .
1.50
.
1.50
 .
.
1.51
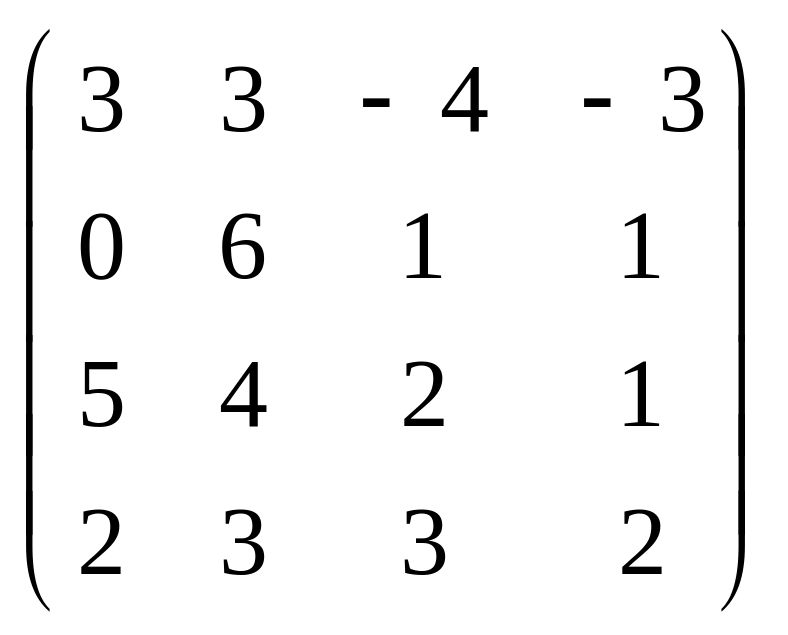 .
1.52
.
1.52
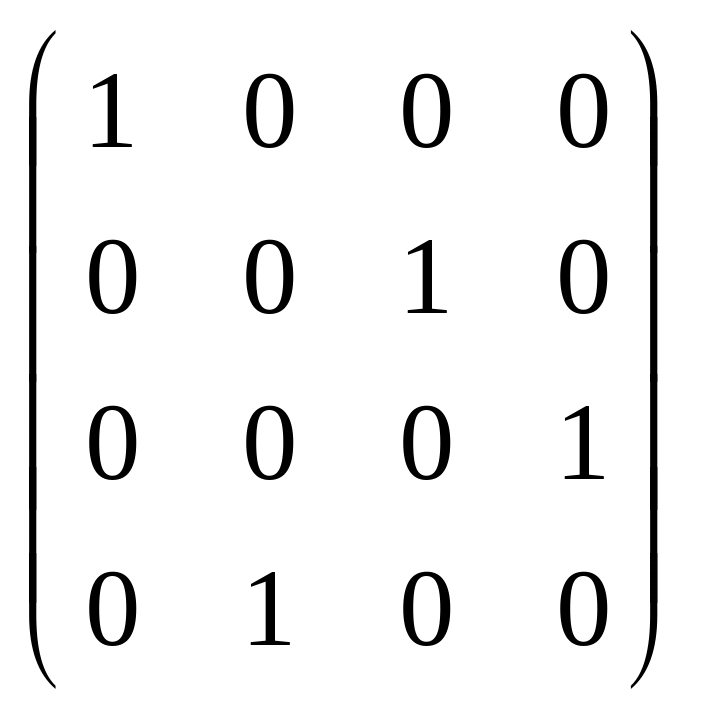 .
.
В задачах 1.53-1.58 решить матричные уравнения.
1.53
![]() .
1.54
.
1.54![]() .
.
1.55
![]() .
1.56
.
1.56![]() .
.
1.57а)
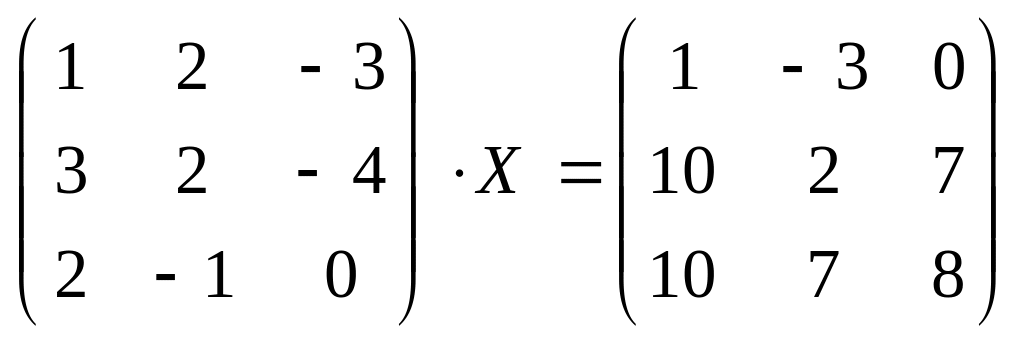 ;
б)
;
б)
![]() .
.
1.58а)
![]() ;
б)
;
б)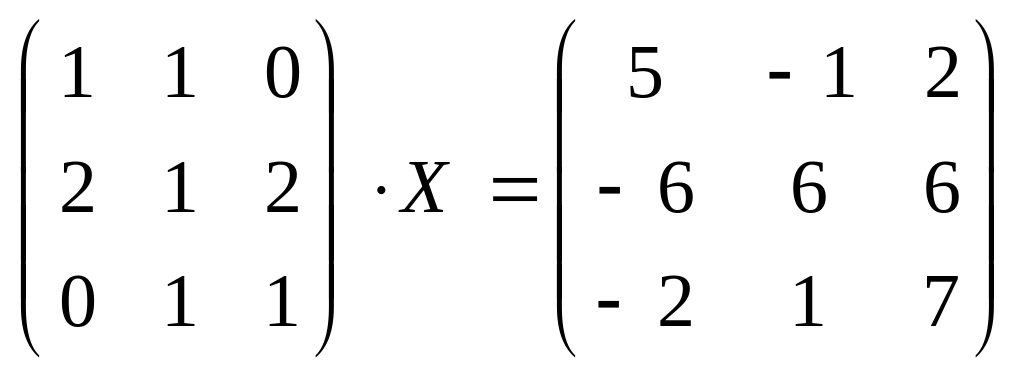 .
.
