Задание к лабораторной работе

Для альтернатив выделенных в лабораторной работе № 4 вычислить весовые коэффициенты при частных критериях методами ранжирования и непосредственной оценки. Учитывая полученные коэффициенты выбрать наилучшую альтернативу, рассчитав интегральный критерий на основе аддитивных преобразований.

Пример выполнения задания

Метод ранжирования.

Пусть оценивают альтернативы три эксперта. Число рангов равно числу исследуемых частных критериев и равно двум.

Значения Ci вычисляем по формуле (6.3).

, .

Значения весовых коэффициентов вычисляем по формуле (6.4).

,

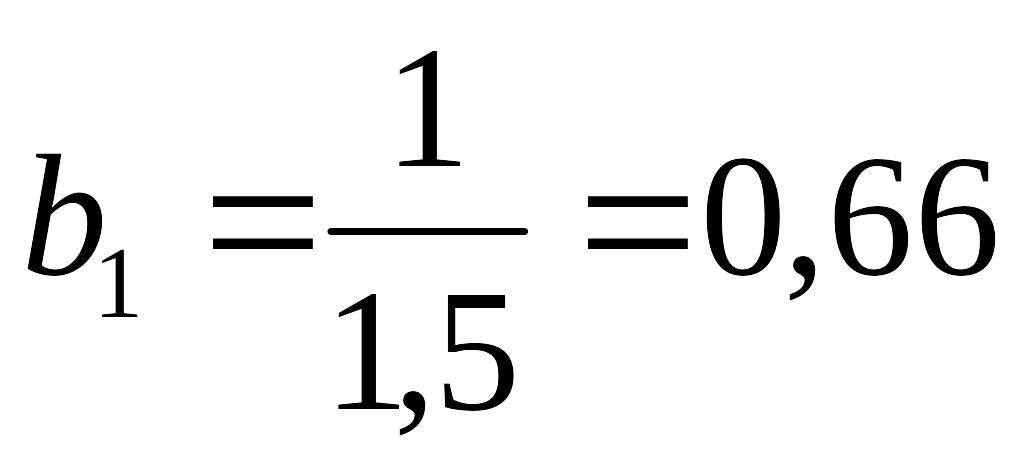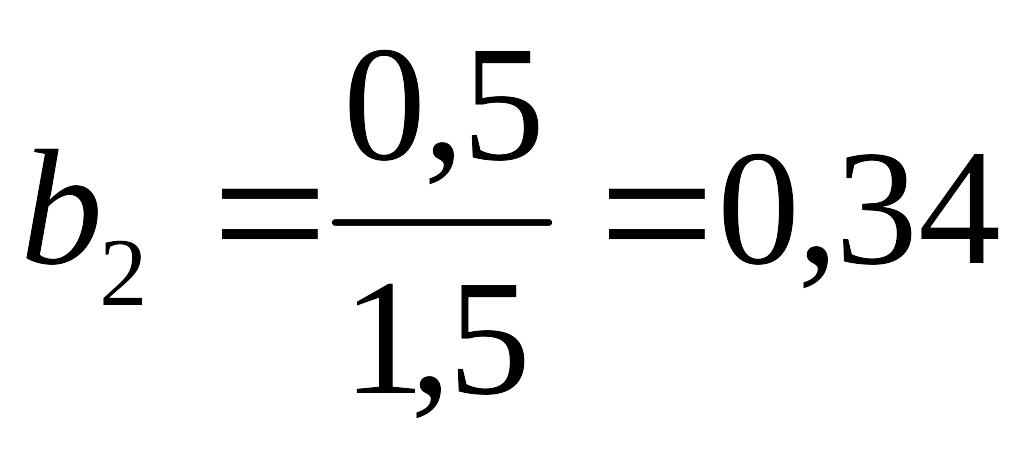
Проверка: b₁ + b₂ = 1.

Эксперты	Частные критерии выбора
	Стоимость внедрения	Срок реализации
1. Иванов	2	1
2. Сидоров	1	2
З. Петров	1	2
Сумма рангов	4	5
Конечный ранг показателя ri	1	2
Значение Ci	1	0,5
Значение весового коэффициента bi	0,66	0,34

Метод непосредственной оценки.

Пусть оценку критериев производят те же три эксперта и ими были даны следующие оценки по пятибалльной шкале:

Эксперты (j)	Оценки показателей Сi		Сумма оценок
	Стоимость внедрения	Срок реализации
1. Иванов	3	5	8
2. Сидоров	4	3	7
3. Петров	5	2	7

Определим вес каждого показателя в системе остальных критериев, оцененных каждым экспертом по формуле (6.5)

, , , , , .

Оценка Cij	C11	C12	C13	C21	C22	C23
	3	4	5	5	3	2
Весовой коэффициент bij	b11	b12	b13	b21	b22	b23
	0,38	0,57	0,71	0,63	0,43	0,29

Далее по формуле (6.6) вычисляем значения весовых коэффициентов b_i.

, .

Проверка: b₁ + b₂ = 1.

Лабораторная работа № 7 Определение весовых коэффициентов интегрального критерия методами последовательных и парных сравнений (Саати)

Цель работы. Изучение методов повышения достоверности значений весовых коэффициентов частных критериев, объединенных в обобщенный аддитивный критерий.

Методические указания

1. Метод последовательных сравнений

Этот метод предназначен для повышения достоверности информации, полученной Методами ранжирования или непосредственной оценки. Метод последовательных сравнений рекомендуется применять в тех случаях, когда число частных критериев не превышает 7.

В данном методе производится сравнение (n – 2) пар специально подобранных абстрактных объектов. Эксперт фактически должен определить, какой из двух объектов лучше: обладающий только i-м свойством или совокупностью из i+1, i+2,…, n свойств.

Применение этого метода удобно записать в виде следующего алгоритма.

1. Проводится ранжирование частных критериев и присваивание первоначальных значений коэффициентам С_ij методами ранжирования или непосредственной оценки (см. лаб. раб. № 6).

2. Для i = 1, 2, …, (n - 2) выясняется, будет ли объект, обладающий только i-м критерием, важнее объекта, обладающего совокупностью критериев, получивших меньшую оценку (i+1, i+2, …, n), и составляется набор отношений:

, (7.1)

где [R] - операция отношения; [R] ≡ ">", если i-й показатель более ценен, чем вместе взятые показатели с меньшим рангом; [R] ≡ "<", если i-й показатель менее ценен, чем вместе взятые показатели с меньшим рангом; [R] ≡ "=", если i-й показатель и совокупность показателей с меньшими рангами имеют одинаковую ценность.

3. Проводится проверка составленных в п.2 отношений на соответствие оценкам С_ij, выбранным в п.1. Если неравенство не выполняется, то либо изменяются значения С_ij для i от (n - 2) до 1 так, чтобы составленные неравенства были истинны и не нарушилась первоначальная ранжировка критериев, либо изменяется знак отношения. Следует заметить, что если начать эту проверку не с конца, а с начала, то на каждом шаге пришлось бы возвращаться и корректировать значения уже рассмотренных коэффициентов, т. к. изменение С_ij может повлечь и нарушение отношений.

4. Проводится масштабирование значений C_ij для получения весовых коэффициентов b_ij (рассчитываются по формуле (6.5)). Окончательные значения весовых коэффициентов b_i, рассчитываются по формуле (6.6) из лабораторной работы № 6.

Пример. Пусть j-й эксперт выставил ряд оценок коэффициентов C_ij, отражающих его мнение об относительной ценности шести частных критериев некоторого объекта. Значения С_ij приведены а таблице 7.1.

Таблица 7.1

ai	a1	a2	a3	a4	a5	a6
Cij	1.0	0.9	0.7	0.6	0.3	0.1

Для уточнения оценок С_ij эксперт сравнивает четыре пары абстрактных объектов, каждый из которых представлен вектором

x = (x₁, x₂, …, x_i, …, x_n),

где x_i = 1 соответствует включению i-го критерия в абстрактный объект;

x_i = 0, если i-й критерий не рассматривается.

Пусть в результате сравнения эксперт получил следующие соотношения:

1) (100000) хуже (011111);

2) (010000) лучше (001111);

3) (001000) хуже (000111);

4) (000100) лучше (000011);

В ходе проверки на соответствие полученных неравенств и оценок коэффициентов С_ij (табл. 7.1) экспертом корректируются значения оценок для 1-го и 2-го критериев таким образом, чтобы выполнялись соотношения (1) и (2) и не нарушалась ранжировка критериев. По окончании проверки путем масштабирования по формуле (6.5) эксперт получает значения коэффициентов b_ij. Результаты корректировки и масштабирования сведены в таблице 7.2.

Таблица 7.2

ai	a1	a2	a3	a4	a5	a6
Cij	2.5	2.0	0.7	0.6	0.3	0.1
bij	0.4	0.32	0.11	0.1	0.05	0.02