2. Метод непосредственной оценки.
При использовании этого метода весь набор критериев оценивается каждым экспертом эвристически из какого-либо количества баллов, например, по десятибалльной системе, или сразу весовым коэффициентом от 0 до 1, согласно проведенному упорядочению по важности. Значения оценок i-гo показателя j-м экспертом Cij должны находиться в невозрастающей зависимости от ранга. Одинаковым по важности критериям должны присваиваться одинаковые оценки.
Тогда вес i-го показателя в системе остальных критериев, оцененных j-м экспертом, равен:
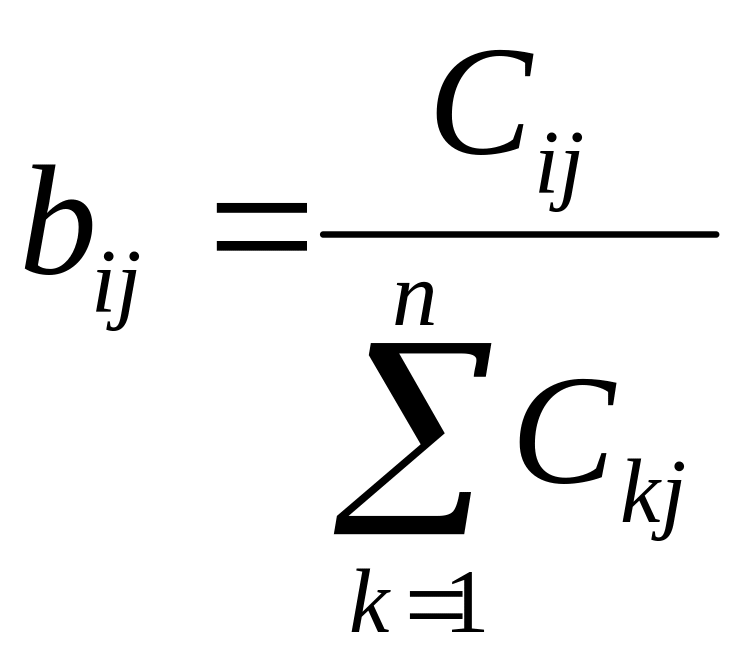, (6.5)
где Сij - оценка i-го показателя j-м экспертом.
Среднее значение весового коэффициента i-гo частного критерия определяется формулой:
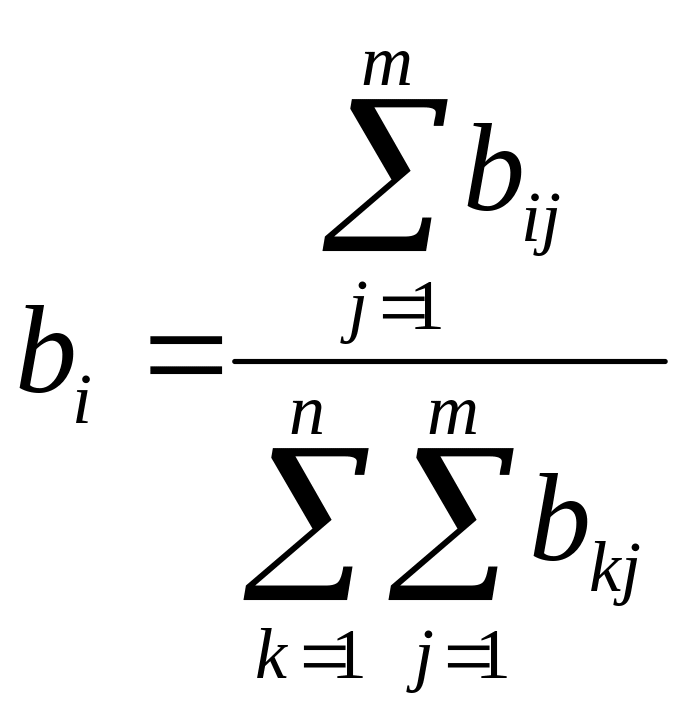. (6.6)
Рассмотрим использование метода непосредственной оценки для примера, рассмотренного выше. Дана оценка по трехбалльной системе (для упрощения, в целых числах).
Таблица 6.2
Эксперты (j) |
Оценки показателей Сi |
|||
Объем ОЗУ |
Быстродействие |
Стоимость |
|
|
1. Иванов |
0 |
3 |
1 |
4 |
2. Сидоров |
1 |
2 |
3 |
6 |
3. Петров |
2 |
2 |
1 |
5 |
Значения весовых коэффициентов bij приведены в табл.6.3.
Таблица 6.3
Оценка Cij |
C11 |
C12 |
C13 |
C21 |
C22 |
C23 |
C31 |
C32 |
C33 |
0 |
1 |
2 |
3 |
2 |
2 |
1 |
3 |
1 |
|
Весовой коэффициент bij |
b11 |
b12 |
b13 |
b21 |
b22 |
b23 |
b31 |
b32 |
b33 |
0 |
0.17 |
0.4 |
0.75 |
0.33 |
0.4 |
0.25 |
0.5 |
0.2 |
При этом:
= 0.57; 
= 1.48; 
= 0.95.
= 0.57 + 1.48 + 0.95 = 3.
Окончательные значения весовых коэффициентов bi каждого i-гo критерия:
b1 = 0.19; b2 = 0.49; b3 = 0.32.
Проверка: b1 + b2 + b3 = 0.19 + 0.49 + 0.32= 1.
Ранжирование указывает лишь на относительную значимость показателей, не выявляя их абсолютной важности, поэтому обычно применяют первую его часть (упорядочение частных критериев по важности) в совокупности с другими методами.
Контрольные вопросы и задания
1. С какой целью при построении интегрального критерия вводятся весовые коэффициенты?
2. Поясните простейший метод получения весовых коэффициентов для частных критериев?
3. Поясните принцип нахождения весовых коэффициентов частных критериев методом ранжирования.
4. Поясните принцип нахождения весовых коэффициентов частных критериев методом непосредственной оценки.