Лабораторная работа № 6 Определение весовых коэффициентов интегрального критерия методами ранжирования и непосредственной оценки

Цель работы. Изучение простейших методов получения значений весовых коэффициентов частных критериев, объединенных в обобщенный аддитивный критерий.

Методические указания

Определение весовых коэффициентов при частных критериях составляет особую задачу при построении интегрального критерия на основе аддитивных или мультипликативных преобразований. Оно обычно производится на основе опроса нескольких экспертов, по результату которого можно составить матрицу индивидуальных оценок, например, в следующем виде:

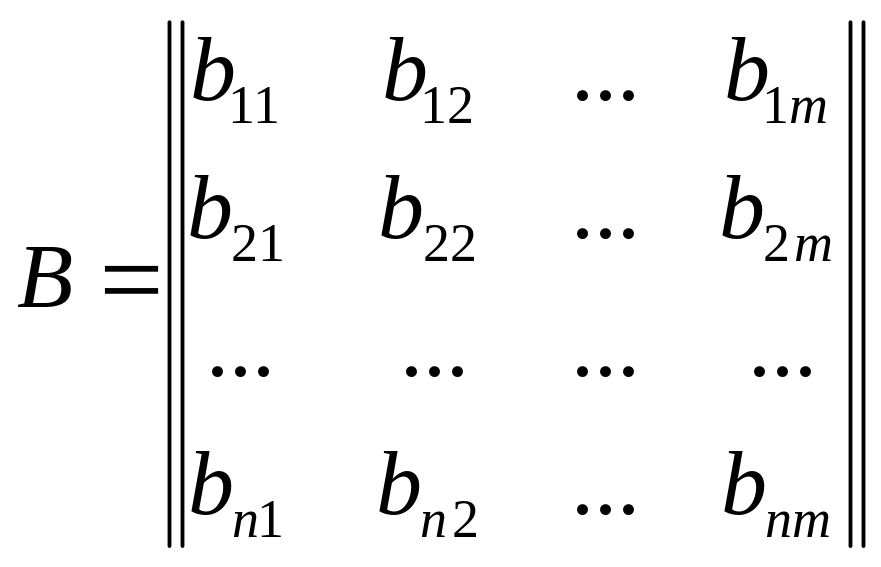или B = [b_ij], i = 1,2,…,n; j = 1,2,…,m.

В этой матрице i-я строка соответствует множеству значений i-го коэффициента, данных всеми экспертами, а j-й столбец - набору значений весов, данных j-м членом совета (m - число экспертов, n - число частных критериев). Задача фактически заключается в преобразовании такой матрицы в вектор-столбец окончательных коэффициентов (b₁, b₂, ..., b_n)^Т во взвешенной сумме

(6.1)

Простейший способ преобразования такой матрицы в вектор - нахождение среднего арифметического по столбцам (при условии, что компетентность экспертов считается одинаковой). Однако, обычно применяются более сложные методы и их сочетания, в которых экспертам предлагается не вычислять значения весов, но определять взаимную или абсолютную приоритетность частных критериев.

Кроме того, может применяться так называемый метод Дельфы, который проводится в несколько туров. На каждом из них подсчитывается средняя оценка и сообщается экспертам. Экспертов, давших крайние оценки, просят обосновать свое мнение. Эта процедура повторяется до тех пор, пока оценки не сойдутся к достаточно узкому интервалу (более подробно этот метод будет рассмотрен в следующих Лабораторных работах).

1. Метод ранжирования.

Метод предусматривает установление относительной значимости критериев q₁,q₂,…,q_n. Каждым экспертом производится ранжирование, то есть упорядочение критериев q_i в зависимости от их важности: наиболее важному по его мнению показателю присваивается первый ранг, а наименее важному - последний. Обычно число рангов равно числу исследуемых частных критериев.

Если эксперт помещает на одно место несколько одинаково важных критериев, то им присваивается стандартизованный ранг, представляющий собой среднее значение мест, падающих на показатели с одинаковой значимостью. Общее число рангов должно быть равно n.

Затем для каждого частного критерия q_i подсчитывается сумма рангов, присужденных ему экспертами. Критерию, набравшему минимальную сумму, окончательно присваивается первый ранг, критерию, получившему максимальную сумму, - последний.

Сумма рангов при ранжировании n критериев равна сумме чисел натурального ряда:

. (6.2)

Вычисление весовых коэффициентов производится в предположении линейной зависимости между рангом и относительной ценностью критерия (чем меньше значение ранга, тем более важен критерий). В зависимости от ранга критерия определяется относительная оценка i-гo критерия

. (6.3)

Затем путем масштабирования осуществляется переход к весовым коэффициентам b_i, по формуле

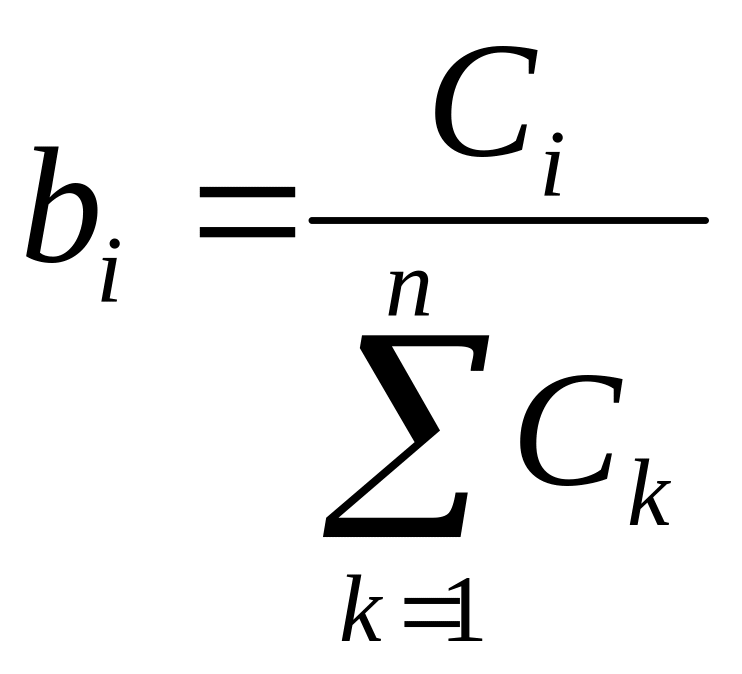, где . (6.4)

В качестве примера в табл. 6.1 приведены результаты ранжирования нескольких характеристик ПЭВМ при выборе конфигурация для решения некоторой задачи. При выборе конфигурации ПК возможны варианты, покупка ЭВМ для программирования, для обработки текстов и т.п.

Таблица 6.1

Эксперты	Частные критерии выбора
	Объем ОЗУ	Быстродействие	Стоимость
1. Иванов	3	1	2
2. Сидоров	3	2	1
З. Петров	1.5	1.5	3
Сумма рангов	7.5	4.5	6
Конечный ранг показателя ri	3	1	2
Значение Ci	0.33	1	0.66
Значение весового коэффициента bi	0.17	0.5	0.33