Полная проверка прочности. Опасные сечения и опасные точки.

Для проверки на прочность при изгибе по действующим на балку внешним нагрузкам строят эпюры изменения внутренних усилий по ее длине и определяют опасные сечения балки, для каждого из которых необходимо провести проверку прочности.

При полной проверке прочности таких сечений будет, как минимум, три (иногда они совпадают):

1. сечение, в котором изгибающий момент М_х - достигает своего максималь­ного по модулю значения, - именно по этому сечению подбирают сечение всей балки;

2. сечение, в котором поперечная сила Q_y, достигает своего максимального по модулю значения;

3. сечение, в котором и изгибающий момент М_x и поперечная сила Q_y дости­гают по модулю достаточно больших величин.

В каждом из опасных сечений необходимо, построив эпюры нормальных и касательных напряжений, найти опасные точки сечения (проверка прочности проводится для каждой из них), которых также будет, как минимум, три:

1. точка, в которой нормальные напряжения , достигают своего макси­мального значения, - то есть точка на наружной поверхности балки наиболее удаленная от нейтральной оси сечения;

2. точка, в которой касательные напряжения достигают своего макси­мального значения, - точка, лежащая на нейтральной оси сечения;

3. точка, в которой и нормальные напряжения, и касательные напряжения, достигают достаточно больших величин (эта проверка имеет смысл для сечений типа тавра или двутавра, где ширина резко изменяет свое значе­ние).

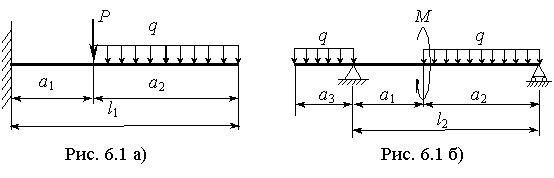
Пример 11.

Для заданных двух схем балок (рис.6.39) требуется написать выражения , для каждого участка в общем виде, построить эпюры , , найти и подобрать: для схемы а) деревянную балку круглого поперечного сечения при МПа; для схемы б) стальную балку двутаврового поперечного сечения при МПа. При М = 20 кН/м, Р = 20 кН, q = 8 кН/м, м, м, , , .

а) б)

Рис.6.39

Решение.

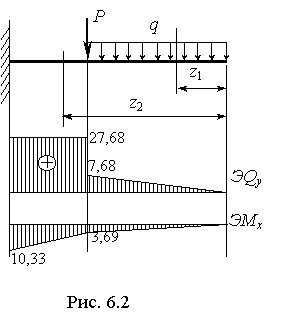
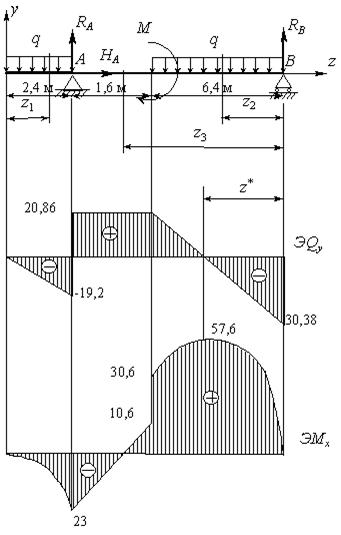
а) б)

Рис.6.40

Схема а).

1. Для определения внутренних усилий , используем метод сечений. Определим количество участков: граничными точками участков являются точки приложения сосредоточенных сил и моментов, а также точки начала и конца распределенной нагрузки. В данной задаче консольная балка имеет два участка. Рассечем последовательно со свободного конца каждый из них. Отбрасывая часть балки, включавшую защемление, определим внутренние силовые факторы в сечении. Поперечная сила равна алгебраической сумме проекций сил, приложенных к отсеченной части на поперечную ось (ось у), изгибаюший момент равен алгебраической сумме моментов, возникающих на отсеченной части относительно оси х в сечении. При определении знаков, используем следующее правило: поперечная сила положительна, если отсеченная часть стремится повернуться по часовой стрелке относительно, точки сечения, изгибающий момент положителен, если балка становится вогнутой.

Запишем выражения для внутренних силовых факторов и сосчитаем их значения в граничных точках участков (рис.6.40,а).

1 участок: м

кН;

.

, кН;

, кНм.

II участок: м

;

,

кН, кН;

кНм, кНм.

2. Построим эпюры внутренних силовых факторов, откладывая вычисленные значения на графике (рис.6.40,а). Соединим полученные точки прямыми линиями на участках, где аргумент z входит в первой степени и параболами, где z входит во второй степени. Таким образом, эпюра изгибающего момента на первом участке будет криволинейной, остальные участки эпюр будут прямолинейными. Определим опасное сечение балки, т.е. сечение, в котором изгибающий момент достигает наибольшего по модулю значения. Опасным сечением будет сечение на опоре, где кН/м.

3. Диаметр круглого сечения найдем из условия прочности

,

, ,

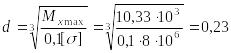м.

Схема б).

1. Для балки, лежащей на двух шарнирных опорах (рис.6.40,б), найдем опорные реакции R_А, Н_А, R_В . Запишем уравнения равновесия статики:

;

;

.

;

.

Для проверки правильности определения реакций запишем еще одно уравнение равновесия, которое должно тождественно удовлетвориться при правильно найденных значениях реакций.

,

.

Балка имеет три участка, рассечем каждый из них.

I участок:

кН;

.

, кН;

, кНм.

II участок: м

;

,

кН, кН;

, кНм.

2. Построим эпюры, соединяя полученные значения и . На втором участке эпюра имеет максимум при . Для определения величины максимального момента приравняем нулю выражение поперечной силы на участке, определим величину и подставим ее в выражение изгибающего момента:

,

м,

кНм.

Двутавровое сечение найдем из условия прочности, определив необходимую величину момента сопротивления

,

.

Из сортамента прокатной стали (ГОСТ 8239-72) выберем двутавр с см³,

, см³.

Перемещения при изгибе балок

Дифференциальное уравнение изогнутой оси упру­гой балки

При расчете балок на изгиб инженер интересуется не только напряже­ниями, возникающими от действия внешних сил, но и перемещениями от действия тех же сил. Одно из требований к элементам конструкций, чтобы перемещение не превосходило некоторого допусти­мого значения, обусловленного требованиями эксплуатации. Это условие называется условием жесткости либо конструктивной прочности.

При расчете строительных и машиностроительных конструкций на жесткость (в большинстве случаев по прогибам, по углам поворота) должно соблюдаться условие

т.е. относительный прогиб f/l, подсчитанный при действии нормативных нагрузок, не должен превышать установленный нормами предельный прогиб 1/n_o для данного вида конструкции.

Для обеспечения нормальной работы подшипников скольжения и роликовых подшипников качения иногда ставится дополнительное условие жесткости – ограничение угла поворота опорных сечений:

.

Допускаемый угол поворота берется из соответствующих справочников. В среднем составляет 0,001 рад.

Рассмотрим плоский чистый изгиб балки (рис. 6.41, а).

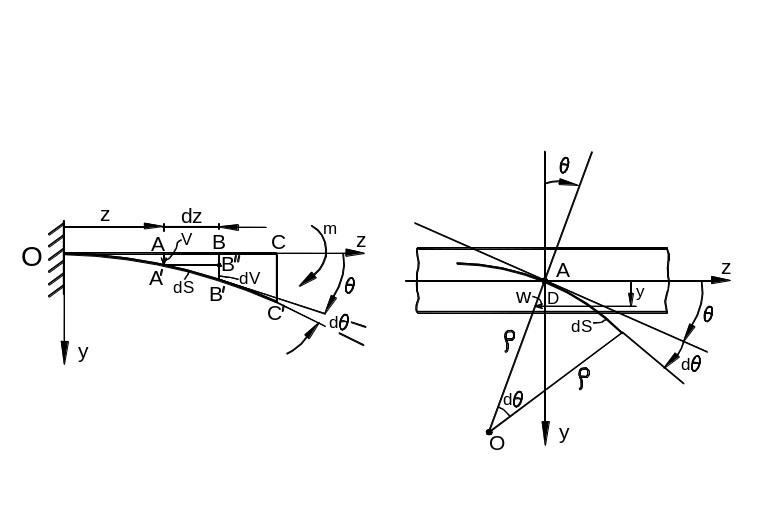
а) б)

Рис. 6.41

В результате действия изгибающего момента m ось балки ОС изгибается и занимает некоторое положение ОС'. Произвольная точка А оси балки, характе­ризуемая координатой , перемещается в новое положение А'. Перемещение, изображаемое направленным отрезком , назовем прогибом балки для точки А с координатой и обозначим v. Проведем в точке А' касательную к изогнутой оси балки. Она образует с осью угол .

Из рис. 6.41,б видно, что этот угол в силу взаимной перпендикулярности сто­рон в точности равен углу поворота поперечного сечения. При изменении , т.е. при переходе к другим точкам оси балки, прогиб v и угол поворота поперечного сечения изменяется. Следовательно, они являются функциями :

(19)

Горизонтальное перемещение w произвольной точки D поперечного се­чения на расстоянии от оси балки равно:

(20)

Из треугольника А'В'В" следует, что первая производная от функции прогиба :

(21)

равна тангенсу угла наклона касательной к изогнутой оси балки в точке А с координатой . Из этого же треугольника получаем

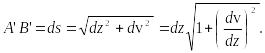(22)

Из рис. 6.41,б находим где - радиус кривизны дуги . Следовательно, кривизна изогнутой оси в точке А равна:

(23)

Дифференцируя (21) по и учитывая (19), (22), (23), получаем:

откуда

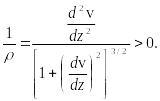(24)

Формула для кривизны балки

для положительных значений . В нашем примере на рис. 6.41 изгибающий момент . Поэтому эту формулу мы должны использовать в виде:

(25)

Приравнивая (24), (25), получаем точное дифференциальное уравнение изогнутой оси балки:

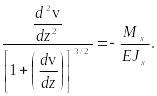(26)

Если прогибы балки малы по сравнению с ее линейными размерами, то и углы поворота сечений - малые величины и, согласно (21)-(24), можно считать:

, ,

Тогда дифференциальное уравнение (26) упрощается и принимает вид

(27)

Уравнение (27) носит название приближенного дифференциального уравнения изогнутой оси упругой балки. Оно получено для случая чи­стого изгиба, но может быть использовано и при поперечном, когда мо­мент является функцией .

Интегрируя (27), получаем:

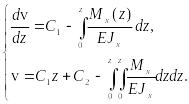(28)

Произвольные постоянные C₁, С₂ в (28) имеют простой геометрический смысл. Обозначим через прогиб и угол поворота cечения соответственно в начале координат при . Тогда при из (10) получаем:

Величины называют начальными параметрами задачи по определению перемещений в балках.

Соотношения (28) запишем в виде

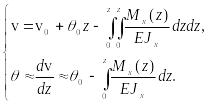(29)

Так как

то решение (29) можно записать в виде:

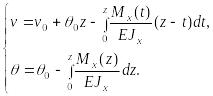
В соответствии с дифференциальными зависимостями Журавского

(30)

Дифференцируя (27) дважды по и используя зависимости (30), находим

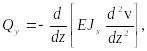(31)

. (32)

При постоянной жесткости получаем

(33)

(34)

Уравнения (32), (34) представляют собой вторую форму дифферен­циальных уравнений изогнутой оси балки четвертого порядка.

Общее решение неоднородного уравнения (34) имеет вид

(35)

где - его частное решение. Постоянные находятся из условий на опорах балки. Эти условия называют граничными или краевыми.

Рассмотрим типичные условия закрепления или опирания балок (рис. 6.42). Изогнутая ось балки изображена тонкой линией.

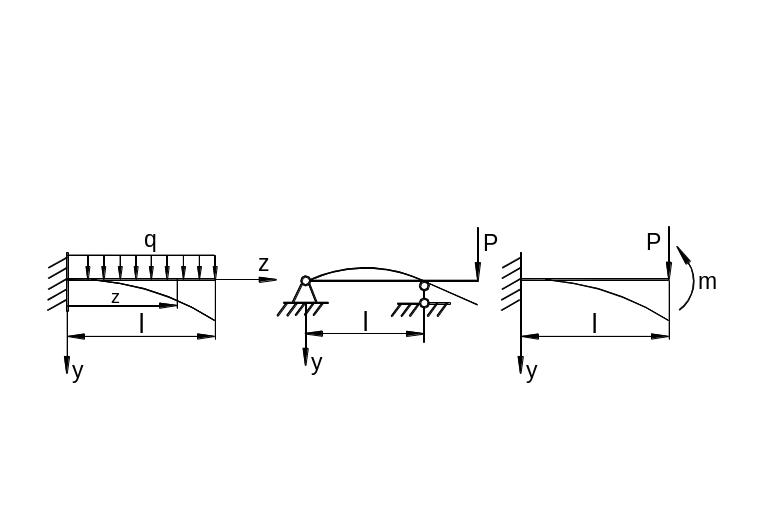
а) б) в)

Рис. 6.42

а) Край балки жестко защемлен (рис. 6.42,а). При z = 0 на защемленном крае прогиб и угол поворота сечения равны нулю, т.е.

б) Край балки свободен от закрепления и нагрузки (рис.6.42,а). В этом случае при равны нулю: момент и перерезывающая сила:

в) Край балки шарнирно закреплен либо свободно опёрт (рис. 6.42,б). При z = 0 край балки шарнирно закреплен. Здесь прогиб и момент равны нулю, т.е.

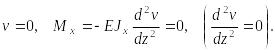
При балка свободно лежит на опоре. Прогиб равен нулю, но изгибающий момент в сечении балки отличен от нуля. Поэтому здесь только одно граничное условие .

г) Незакрепленный край балки с действующими сосредоточенными силой и моментом (рис. 6.42,в).

В этом случае при имеем статические граничные условия:

Пределы применимости приближенной теории из­гиба балок

При выводе дифференциального уравнения изогнутой оси балки (28) выражение для кривизны балки было выбрано приближенно. Выясним степень точности приближенного уравнения (27). Для этого рассмотрим задачу о чистом изгибе консольной балки (рис. 6.43).

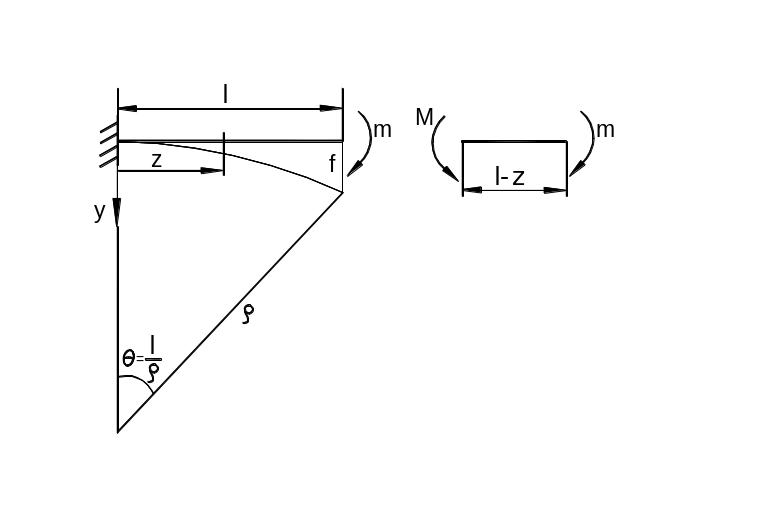
Рис. 6.43

В этом случае и поэтому Из рис. 6.43 прогиб на конце консоли:

Разложим косинус в ряд и ограничимся тремя первыми элементами:

Выражение для прогиба f принимает вид:

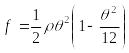
или с учетом и (7):

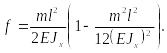(36)

Дадим теперь приближенное решение задачи. Интегрируя уравнение

при получаем:

Так как при прогиб , угол поворота , то

При на конце консоли прогиб:

(37)

Сравнивая решения (36), (37), находим:

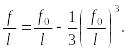
Удовлетворимся при определении прогибов по приближенной теории точ­ностью в 3%. Полагая

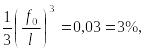
получаем:

Таким образом, приближенное дифференциальное уравнение (27) изо­гнутой оси упругой балки дает достаточную точность решения задачи даже в том случае, когда прогиб составляет 30% от длины стержня. Та­кие прогибы возможны только у очень гибких балок большой длины или очень малой толщины типа гибкой стальной линейки.

Интегрирование дифференциального уравнения изогнутой оси балки методом начальных пара­метров А. Н. Крылова

Рассмотрим балку, нагруженную силами и моментами (рис. 6.44). Силы , считаем положительными, если они направлены в положительном направлении координатной оси у, т.е. вниз. Момент считаем положительным, если он вращает сечение балки против часовой стрелки, когда мы смотрим на него с конца положительной оси , ортогональной к плоскости . В этом случае прогибы любой точки оси стержня с координатой z направлены вниз по оси у.

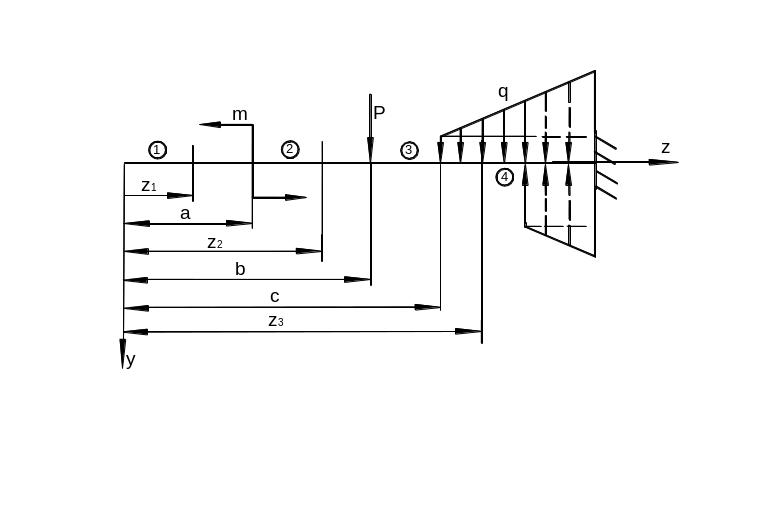
Рис. 6.44

Балку по длине можно разбить на несколько участков, на которых аналитические выражения изгибающих моментов будут различны.

Границей этих участков являются те сечения, над которыми к балке приложены сосредоточенные силы Р, момент m либо меняется характер нагружения так, как в сечении , с которого начинается действие распределенной нагрузки .

Интегрируем дважды дифференциальное уравнение изогнутой оси балки (27):

В результате получаем:

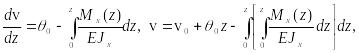(38)

где - прогиб и угол поворота сечения в начале координат при , называемые начальными параметрами задачи по определению перемещений. Вычислим в (38) интеграл:

при одновременном действии считая жесткость при изгибе постоянной величиной. Для этого найдем аналитические выражения момента для двух сечений от каждого внешнего силового воздействия. Пусть первое сечение z лежит левее рассматриваемой внешней силы или момента, а второе - правее. Тогда получаем (см. рис. 6.44):

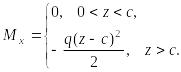
Полагая последовательно при почленном интегрировании , получаем:

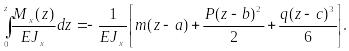
Интегрируя полученное выражение еще раз, найдем:

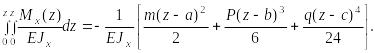
Подставляя полученные выражения интегралов в (38), получим фор­мулы:

(39)

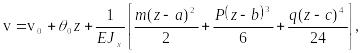(40)

называемые универсальными для угла поворота сечения и прогиба точки оси балки.

Если распределенная нагрузка не является постоянной, то ее можно разложить в ряд Тейлора в окрестности значения :

где - факториал числа .

В этом случае после интегрирования (38) получаем:

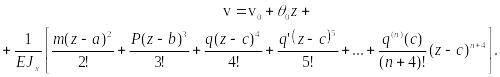(41)

При наличии в балке внутреннего шарнира К в сечении первая производная от прогиба по претерпевает в этом случае скачок на величину (рис. 6.45) так, что:

(42)

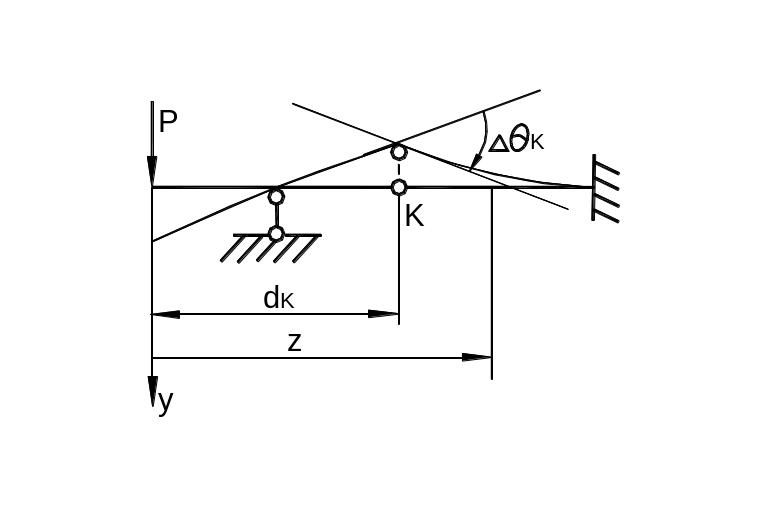
Рис. 6.45

Интегрируя, получаем:

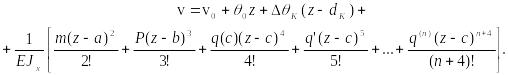(43)

Обобщенные силы , , в (41), (43) повторяются столько раз, сколько они рассматриваются в рассматриваемой задаче. Если распреде­ленная нагрузка не доходит до рассматриваемого сечения с координатой , то ее следует продолжить до этого сечения и добавить точно такую же, но противоположного знака (см. рис. 6.44).

Примечание:

Начало отсчета координаты z необходимо брать только на левом конце балки.

Порядок расчета по методу начальных параметров:

Чтобы определить перемещения методом начальных параметров надо:

1. Определить опорные реакции.

2. Выбрать начало отсчета.

3. Определить начальные параметры из условий закрепления.

4. Подсчитать перемещения линейные или угловые, пользуясь формулами методов начальных параметров.

Простейшие статически неопределимые задачи при изгибе. Метод сравнения (наложения) пере­мещений

Рассмотрим простейшую один раз статически неопределимую балку (рис. 6.46).

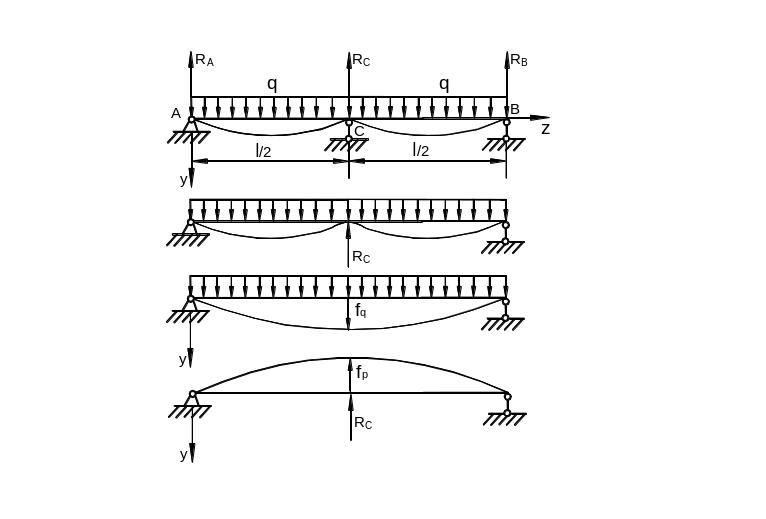
Рис. 6.46

Прогиб балки над опорой С равен нулю и его можно, в силу принципа независимости действия сил, представить как сумму перемещений от рас­пределенной нагрузки и сосредоточенной силы :

Используя известные решения, имеем:

Следовательно,

откуда

Из уравнений равновесия:

находим опорные реакции

В поперечном сечении

Рис. 6.47

Экстремальный момент возникает в сечении с координатой , которая находится из условия:

откуда Максимальный момент

Он меньше, чем момент над средним сечением при :

На рис. 6.47 построены эпюры .

Расчет на прочность простейших статически неопределимых балок методом допускаемых нагрузок

Рассмотрим простейшую статически неопределимую балку (рис. 6.48,а).

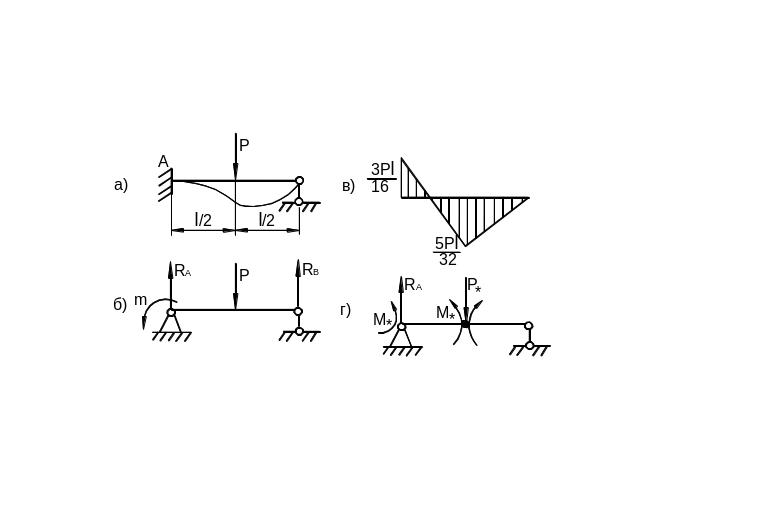
Рис. 6.48

Расчет на прочность по допускаемым напряжениям состоит в том, чтобы найти и потребовать . Для этого сначала необходимо раскрыть статическую неопределимость задачи. На рис. 6.48,б изображена эквивалентная балка, в которой момент m должен быть подобран так, чтобы угол поворота в опоре А обращался в нуль как и в исходной схеме балки (рис. 6.48,а).

Вычислим угол поворота в опоре А:

откуда находим:

Максимальный момент возникает в защемлении (рис. 6.48, в):

Таким образом, условие прочности по допускаемым напряжениям (или расчетному сопротивлению) дает:

откуда

Предельная нагрузка упругого состояния, при которой впервые в бал­ке возникает пластическая деформация, равна:

Первый пластический шарнир образуется в защемлении. В этом пластическом шарнире . Однако балка будет испытывать стеснённую пластическую деформацию, пока в середине пролета под силой Р момент также не будет равным и балка превратится в механизм (рис. 6.48, г). Для предельного состояния имеем уравнения равновесия:

откуда следует

Допускаемое значение внешней нагрузки:

Сравнивая и либо и получим, что их отношение:

Статическая неопределимость задачи повышает допустимую нагруз­ку на 12,5%. Для балки прямоугольного сечения . В случае прямоугольника Для данной задачи обнаружива­ется резерв прочности в 69% по сравнению с расчетом по допускаемым напряжениям.

В рассматриваемом примере пластические шарниры образуются в за- щемлении и в сечении под сосредоточенной силой. В случае распределен­ной нагрузки указать сразу сечения, где возникнут пластические шар­ниры, не всегда удается. Рассмотрим простейшую двухпролетную стати­чески неопределимую балку (рис. 6.49). Выше эта задача была реше­на для случая упругого поведения балки и построена эпюра моментов (рис. 6.47).

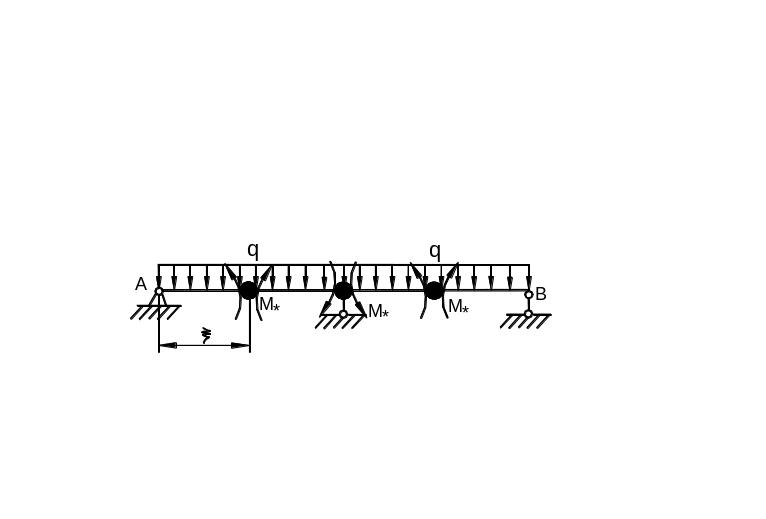
Рис. 6.49

Момент в среднем сечении, при котором в крайних во­локнах возникают пластические деформации:

откуда соответствующая предельная нагрузка равна:

Рассмотрим предельное состояние балки. Первый пластический шарнир образуется над средней опорой. Два других - в сечениях, строго говоря, не совпадающих с сечениями, где действуют максимальные моменты. Обозначим расстояние от левой опоры до первого шарнира в пролете через . Тогда уравнение равновесия балки левее первого и второго шарниров будет иметь вид:

откуда после исключения следует:

Разрушающая предельная нагрузка оказывается зависящей от величиины , т.е. местоположения пластического шарнира в пролете. Дифференцируя данное выражение для по и приравнивая производную нулю, получим:

откуда

Так как , то перед радикалом следует сохранить знак плюс. Тогда В результате получим:

Сравнивая выражения для и , находим:

Следовательно, в данной задаче статическая неопределимость повышает допустимую нагрузку на 45,7%. Если балка имеет прямоугольное сечение, то . Поэтому в данной задаче полное увеличение допускаемой нагрузки составляет т.е. 118,6%. Если заменить в каждом из пролетов распределенную нагрузку q их равнодействующими приложенными в их середине, т.е. при , то получим:

Величина

что отличается от точного решения всего на 2,94%. Для прямоугольного сечения получаем k = 2,25 вместо 2,186.