Касательные напряжения при поперечном изгибе. Главные напряжения при изгибе

В случае поперечного изгиба в сечениях балки возникают не только изгибающий момент, но и поперечная сила. Следовательно, в этом случае в поперечных сечениях бруса возникают не только нормальные, но и касательные напряжения.

Так как касательные напряжения в общем случае распределены по сечению неравномерно, то при поперечном изгибе поперечные сечения балки, строго говоря, не остаются плоскими. Однако при (где h - высота поперечного сечения, l - длина балки) ока­зывается, что эти искажения заметным образом не сказываются на работе балки на изгиб. В данном случае гипотеза плос­ких сечений и в случае чистого изгиба с достаточной точно­стью приемлема. Поэтому для расчета нормальных напряже­ний применяют ту же формулу (5).

Рассмотрим вывод расчетных формул для касательных напря­жений. Выделим из бруса, испытывающего поперечный изгиб, элемент длиной (рис. 6.28,а).

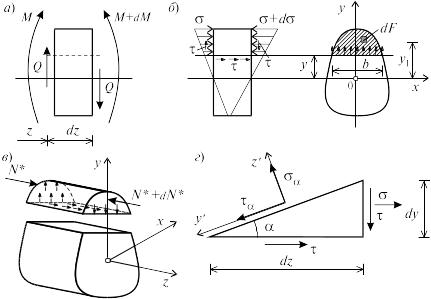
Рис. 6.28

Продольным горизонтальным сечением, проведенным на рас­стоянии y от нейтральной оси, разделим элемент на две части (рис. 6.28,в) и рассмотрим равновесие верхней части, имеющей основание шириной b. При этом с учетом закона парности каса­тельных напряжений, получим, что касательные напряжения в по­перечном сечении равны касательным напряжениям, возникающим в продольных сечениях (рис. 6.28,б). С учетом данного обстоятель­ства и из допущения о том, что касательные напряжения по пло­щади распределены равномерно, используя условие , получим:

,

откуда

. (13)

где - равнодействующая нормальных сил в левом попереч­ном сечении элемента в пределах заштрихованной площади :

. (14)

С учетом (5) последнее выражение можно представить в виде

, (15)

где - статический момент части поперечного сечения, расположенной выше координаты y (на рис. 6.28,б эта область за­штрихована). Следовательно, (15) можно переписать в виде

,

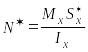откуда

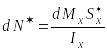. (16)

В результате совместного рассмотрения (13) и (16) получим

,

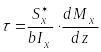или окончательно

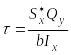. (17)

Полученная формула (17) носит имя русского ученого Д.И. Журавского.

Условие прочности по касательным напряжениям:

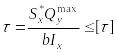, (18)

где -максимальное значение поперечной силы в сечении; - допускаемое касательное напряжение, оно, как правило, равно половине .

Для исследования напряженного состояния в произвольной точке балки, испытывающей поперечный изгиб, выделим из сос­тава балки вокруг исследуемой точки элементарную призму (рис. 6.28,г), таким образом, чтобы вертикальная площадка явля­лась частью поперечного сечения балки, а наклонная площадка составляла произвольный угол относительно горизонта. Прини­маем, что выделенный элемент имеет следующие размеры по координатным осям: по продольно оси - dz, т.е. по оси z; по вер­тикальной оси - dy, т.е. по оси у; по оси х - равный ширине балки.

Так как вертикальная площадка выделенного элемента принад­лежит поперечному сечению балки, испытывающему поперечный изгиб, то нормальные напряжения на этой площадке определя­ются по формуле (5), а касательные напряжения - по формуле Д.И. Журавского (17). С учетом закона парности касательных на­пряжений, легко установить, что касательные напряжения на гори­зонтальной площадке также равны . Нормальные же напряжения на этой площадке равны нулю, согласно уже известной нам гипо­тезе теории изгиба о том, что продольные слои не оказывают дав­ления друг на друга.

Обозначим величины нормальных и касательных напряжений на наклонной площадке через и , соответственно. Принимая площадь наклонной площадки , для вертикальной и горизон­тальной площадок будем иметь и , соответственно.

Составляя уравнения равновесия для элементарной вырезанной призмы (рис. 6.28,г), получим:

,

откуда будем иметь:

;

.

Следовательно, окончательные выражения напряжений на на­клонной площадке принимают вид:

.

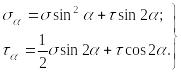Определим ориентацию площадки, т.е. значение , при котором напряжение принимает экстремальное значение. Со­гласно правилу определения экстремумов функций из математиче­ского анализа, возьмем производную функции от и прирав­няем ее нулю:

.

Предполагая , получим:

.

Откуда окончательно будем иметь:

.

Согласно последнему выражению, экстремальные напряжения возникают на двух взаимно перпендикулярных площадках, называ­емых главными, а сами напряжения - главными напряже­ниями.

Сопоставляя выражения и , имеем:

,

откуда и следует, что касательные напряжения на главных пло­щадках всегда равны нулю.

В заключение, с учетом известных тригонометрических тож­деств:

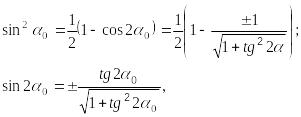
и формулы ,

определим главные напряжения, выражая из через и :

.

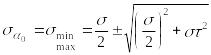Полученное выражение имеет важное значение в теории проч­ности изгибаемых элементов, позволяющее производить расчеты их прочности, с учетом сложного напряженного состояния, присущее поперечному изгибу.

Пример 8.

В качестве примера применения формулы Журавского построим эпюру касательных напряжений для случая прямоугольного поперечного сечения балки (рис. 6.29). Учитывая, что для этого сечения

получаем

где - площадь прямоугольника.

Как видно из формулы, касательные напряжения по высоте сечения меняются по закону квадратической параболы, достигая максимума на нейтральной оси

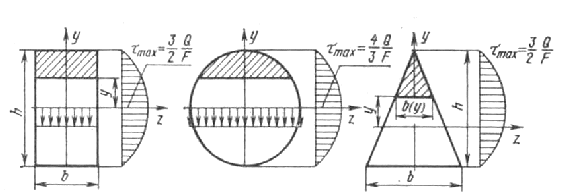
Рис. 6.29

В круглом сечении (рис. 6.29) эпюра касательных напряжений ограничена кривой, имеющей максимум на нейтральной оси. Учитывая, что статический момент полукруга и момент инерции круга

,

получаем

Следовательно, максимальные касательные напряжения в круглом сечении на 33% больше средних напряжений , по которым, например, обычно проводится расчет заклепок.

Для треугольного сечения с основанием b и высотой h (рис. 6.29), имеем

,

Максимальное напряжение имеет место на расстоянии от нейтральной линии, то есть в точках средней линии треугольника.

Пример 9.

Построить эпюру распределения касательных напряжений для балки двутаврового (№ 12) сечения (рис. 6.30), если Q=10 кН.

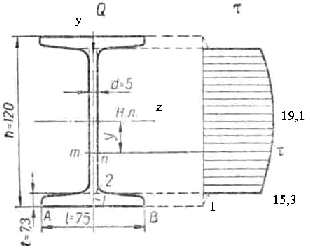
Рис. 6.30

Для построения эпюры схематизируем действительное сечение, представив его в виде трех прямоугольников, как показано на рис. 6.30 пунктиром. Проведя произвольную линию mn, параллельную нулевой линии, и перемещая ее вдоль оси y, обнаруживаем, что при этом напряжения в точках этой линии меняются по параболическому закону, так как мы имеем дело с прямоугольниками. Для построения эпюры касательных напряжений вычислим τ в крайних волокнах (линия AB), в месте сопряжения полки со стенкой (точки 1 и 2, причем будем считать, что они расположены бесконечно близко к границам полки, но лежат по разные стороны от этой границы) и в точках нейтральной линии.

На рис. 6.30 все размеры даны в мм, а напряжения – в МПа.

Для точек линии AB ширина сечения равна l, а статический момент равен нулю, так как линия AB не отсекает никакой площади. Таким в точках линии AB касательные напряжения равны нулю.

Для точки 1 статический момент равен

Момент инерции сечения относительно нейтральной оси находим по сортаменту I_z=403 см⁴. Касательное напряжение в точке 1:

Для точки 2 статический момент (с точностью до бесконечно малых величин) остается таким же, но ширина сечения d=0,5 см. Поэтому касательное напряжение в точке 2

Для точек

Следовательно, при переходе от точки 1 к точке 2 касательное напряжение возрастает в 15 раз и на эпюре получается скачок.

Для точек нейтральной линии ширина сечения d=0,5 см, а статический момент следует взять для половины сечения из сортамента S_z^max=38,5 см³. Поэтому

На основании этих данных строим эпюру касательных напряжений для нижней половины сечения. Для верхней половины сечения в силу симметрии профиля относительно оси z эпюра будет симметричной.

Построенная эпюра условна, так как она дает верные значения касательных напряжений только для точек стенки, достаточно удаленных от полок. Вблизи полок касательные напряжения в стенке возрастают, ввиду того, что место сопряжения полки со стенкой является источником концентрации касательных напряжений. В полках же, где отношение высоты к ширине много меньше единицы, возникают касательные напряжения, перпендикулярные направлению Q, и величина их меняется по ширине сечения.

Необходимо отметить также, что формулой Журавского можно пользоваться только в случае прямого изгиба.

При изгибе тонкостенных профилей касательные напряжения определяются по следующей формуле:

где - толщина тонкостенного профиля.

На рис. 6.31 построена эпюра при изгибе тонкостенного двутавра в вертикальной плоскости симметрии. Вследствие симметрии сечения и нагрузки, касательные напряжения в симметричных точках полок двутавра должны быть также симметричны относительно оси y и будут увеличиваться от края к центру по линейному закону:

.

Вдоль стенки τ изменяются по параболическому закону

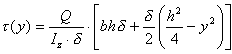
и направлены в ту же сторону, что и сила Q.

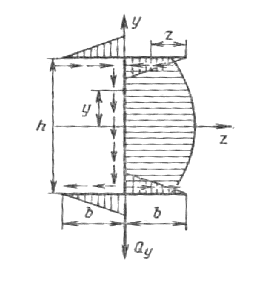
Рис. 6.31

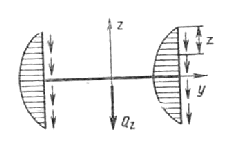
Рис. 6.32

При изгибе двутавра в плоскости второй оси (рис. 6.32) касательные напряжения в стенке равны нулю, а вдоль каждой из полок изменяются по параболическому закону

.

Пример 10.

Для балки из пластичного материала, передающей в опасном сечении изгибающий момент M_max=32 кНм, подобрать двутавровое и прямоугольное сечение ( ), если =160 МПа. Сравнить массы подобранных балок.

Момент сопротивления определяется из условия прочности:

Ближайший стандартный двутавровый профиль подбираем по сортаменту:

Для прямоугольного сечения имеем:

Отношение масс подобранных профилей равно отношению площадей поперечных сечений и составляет 3:1, то есть балка прямоугольного сечения более чем в три раза тяжелее балки двутаврового сечения при условии равной их прочности.

Сделаем несколько замечаний, касающихся расчетов на прочность при прямом поперечном изгибе. В отличие от простых видов деформации, когда в поперечных сечениях стержня возникает лишь один силовой фактор, к которым относятся и изученные выше растяжение (сжатие) и чистый изгиб, прямой поперечный изгиб должен быть отнесен к сложным видам деформации. В поперечных сечениях стержня при поперечном изгибе возникают два силовых фактора: изгибающий момент и поперечная сила (рис.6.33), напряженное состояние является упрощенным плоским, при котором в окрестности произвольно выбранных точек поперечного сечения действуют нормальные и касательные напряжения. Поэтому условие прочности для таких точек должно быть сформулировано на основе какого-либо уже известного критерия прочности.

Однако учитывая, что наибольшие нормальные напряжения возникают в крайних волокнах, где касательные напряжения отсутствуют (рис.6.33), а наибольшие касательные напряжения во многих случаях имеют место в нейтральном слое, где нормальные напряжения равны нулю, условия прочности в этих случаях формулируются раздельно по нормальным и касательным напряжениям

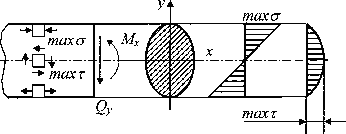Рис.6.33. Распределение нормальных и касательных напряжений по контуру сечения

Рис.6.34. К сравнительной оценке модулей напряжения

Покажем, что доминирующая роль в расчетах на прочность балки, подвергнутой поперечному изгибу, будет принадлежать расчету по нормальным напряжениям. Для этого оценим порядок и на примере консольной балки, показанной на рис. 6.34:

так как

Тогда

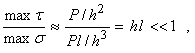
откуда , а поскольку то доминирующим в этом случае будет расчет по нормальным напряжениям и условие прочности, например, для балки из пластичного материала, работающей на прямой изгиб, как и в случае чистого изгиба будет иметь вид:

.