Лекція 2: визначники та їх влативості

1. Визначники квадратних матриць

Визначник є числовою характеристикою квадратної матриці, яка використовується при розв’язанні систем лінійних рівнянь, знаходженні обернених матриць тощо. Визначник квадратної матриці А позначається 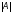або detA.

Визначником матриці першого порядку 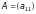називається елемент .

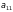Визначником матриці другого порядку називається число, яке розраховується за формулою .

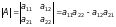Визначником матриці третього порядку називається число, яке обчислюється за формулою:

.

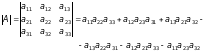За допомогою схеми можна запам’ятати формулу обчислення визначника третього порядку: визначник складається із шести доданків, кожен доданок формули являє собою добуток трьох елементів матриці, вибраних по одному з кожного рядка та кожного стовпчика та позначених на схемі однаковим кольором. Зі знаком «+» беруться три добутки, отримані з лівого малюнку, зі знаком «–» - отримані з правого малюнку. Таке правило обчислення визначників третього порядку називається правилом трикутників.

Приклад 4. Обчислити визначник: .

= =

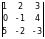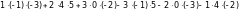=66.

Наведені вище означення визначників є частинними випадками означення визначника n-го порядку. Перед тим, як навести це означення, введемо наступні поняття.

Перестановкою з n елементів називається впорядкований набір перших n натуральних чисел. Кількість перестановок з n елементів дорівнює .

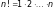Два елементи перестановки утворюють інверсію, якщо більший елемент розташований в перестановці перед меншим.

Перестановка називається парною, якщо містить парну кількість інверсій, та непарною, якщо містить непарну кількість інверсій.

Визначником квадратної матриці А називається число, що дорівнює сумі всіх можливих добутків елементів матриці А, взятих по одному з кожного її рядка та кожного стовпчика, причому доданок береться із знаком “плюс”, якщо перестановка других індексів елементів, що входять в цей добуток, парна, та із знаком “мінус”, якщо ця перестановка непарна, за умови, що перші індекси цих елементів впорядковані за зростанням. Очевидно, кількість доданків при обчисленні визначника n-го порядку дорівнює n!

Із зростанням розмірності визначника кількість доданків сильно збільшується, тому на практиці при обчисленні визначників вищих порядків загальне означення не використовується. Основним методом обчислення таких визначників є метод пониження порядку.

2. Метод пониження порядку визначника

Додатковим мінором 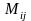до елемента 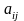квадратної матриці називається визначник матриці, яка утворюється з даної викресленням того рядка і того стовпчика, де знаходиться цей елемент.

Алгебраїчним доповненням до елемента квадратної матриці називається число .

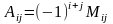Теорема Лапласа. Визначник квадратної матриці дорівнює сумі добутків елементів будь-якого її рядка (стовпчика) на їх алгебраїчні доповнення.

Значення теореми Лапласа полягає в тому, що вона дозволяє звести обчислення визначника n-го порядку до обчислення визначників (n–1)-го порядку.

Приклад 5. Обчислити визначник: .

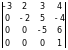Розкладемо визначник, користуючись теоремою Лапласа, за першим стовпчиком.

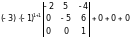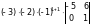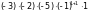= = = = = –30.

Зауваження. З розв’язку видно, що визначник верхньо- або нижньотрикутної матриці дорівнює добутку елементів її головної діагоналі.

Якщо б серед елементів матриці не було б нульових, то використання теореми Лапласа привело б до обчислення чотирьох ненульових доданків з визначниками третього порядку. Отже, в таких випадках перед використанням теореми необхідно спростити елементи визначника, користуючись властивостями визначників.