Задания для самостоятельной работы

n10.7. Исследовать ряд на абсолютную и условную сходимость:

а) ;	б) ;
в) ;	г) ;
д) ;	е) ;
ж) ;	з) .

n10.8. Вычислить сумму ряда с точностью :

а) ;	б) ;
в) ;	г) ;
д) ;	е) ;
ж) ;	з) .

n10.9. Доказать справедливость равенства. (Ответом служит число , получаемое при применении признака Даламбера или признака Коши):

а);	б) ;
в) ;	г) ;
д) ;	е) ;
ж) ;	з) .

Ответы

10. 3. Функциональные ряды Краткие теоретические сведения

Определение 1. Ряд, членами которого являются функции аргумента , определенные на некотором множестве , называется функциональным:

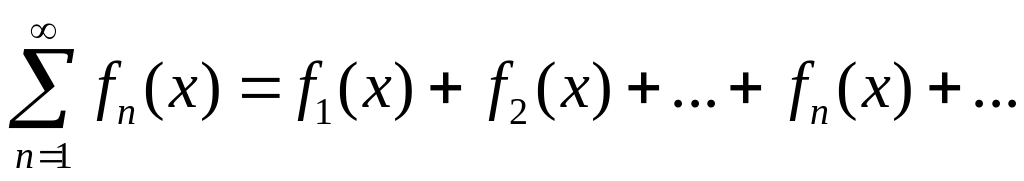
Множество всех значений , при которых функциональный ряд становится сходящимся числовым рядом, называется областью сходимости функционального ряда.

Может случиться, что для некоторых ряд сходится абсолютно, а для некоторых условно.

Для нахождения областей сходимости функциональных рядов можно использовать разложение основных элементарных функций в ряд и достаточные признаки сходимости числовых рядов.

Определение 2. Суммой функционального ряда называется функция , где -я частичная сумма.

Определение 3. Сходящийся в некотором промежутке функциональный ряд 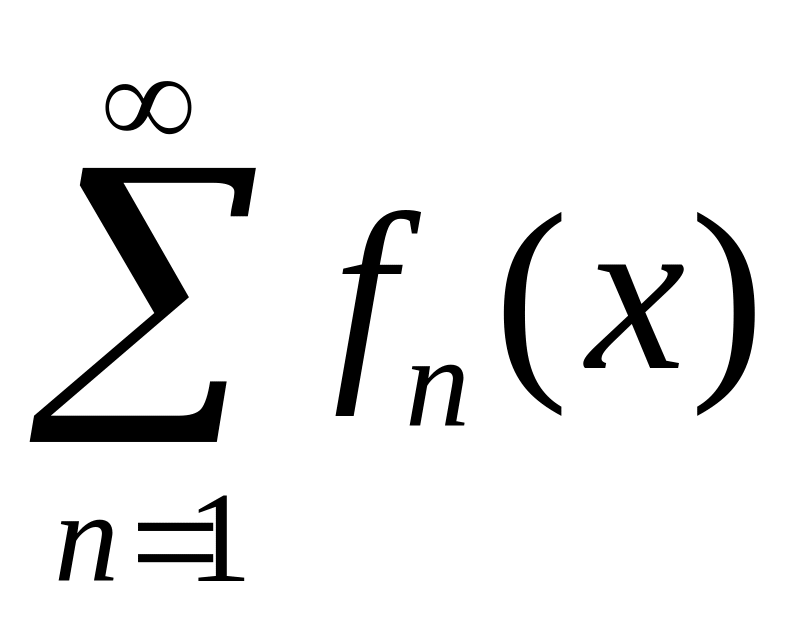называется равномерно сходящимся в этом промежутке, если для любого существует номер , независящий от и такой, что для всех справедливо неравенство одновременно для всех значений рассматриваемого промежутка.

Теорема 1. Если членами функционального ряда являются непрерывные в некотором промежутке функции и в этом промежутке ряд сходится равномерно, то его сумма непрерывна в этом промежутке.

Теорема 2 (признак Вейерштрасса). Если члены функционального ряда в некотором промежутке Е не превосходят по абсолютной величине соответствующих членов сходящегося числового ряда с положительными членами, т.е. если для всех Е: , то данный функциональный ряд сходится в этом промежутке абсолютно и равномерно.

Числовой ряд называется мажорирующим рядом или числовой мажорантой для функционального ряда на промежутке.

Теорема 3. Если членами функционального ряда являются непрерывные на промежутке функции, и ряд сходится равномерно на этом отрезке к функции , то его можно почленно проинтегрировать на этом отрезке: .

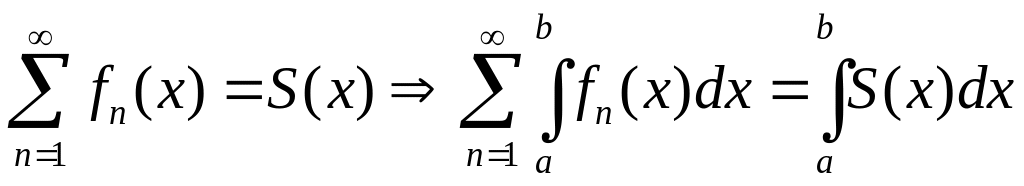Выше сформулированы достаточные условия для почленного интегрирования рядов. Существуют ряды, не удовлетворяющие условиям этой теоремы, но допускающие почленное интегрирование.

Теорема 4. Если в некотором промежутке:

1. функциональный ряд сходится к сумме ;

2. члены 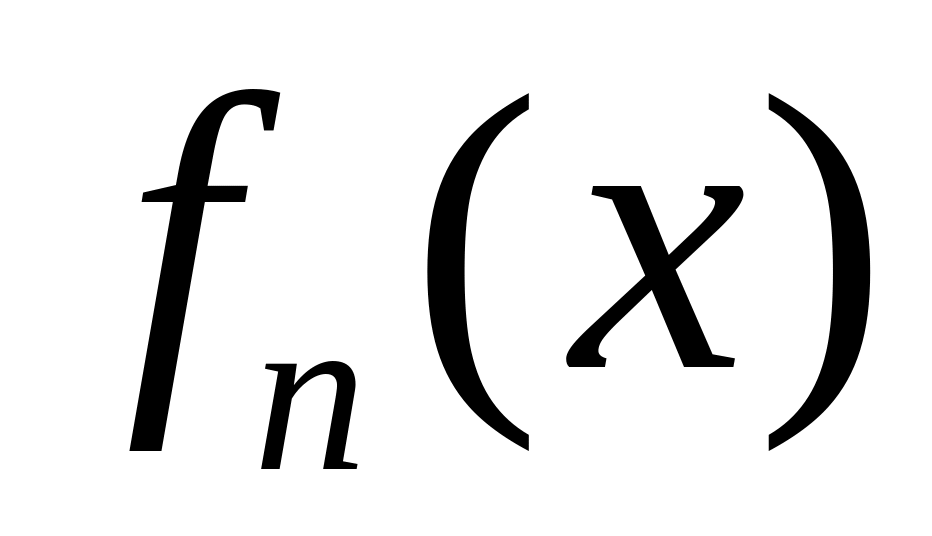данного ряда имеют непрерывные производные ;

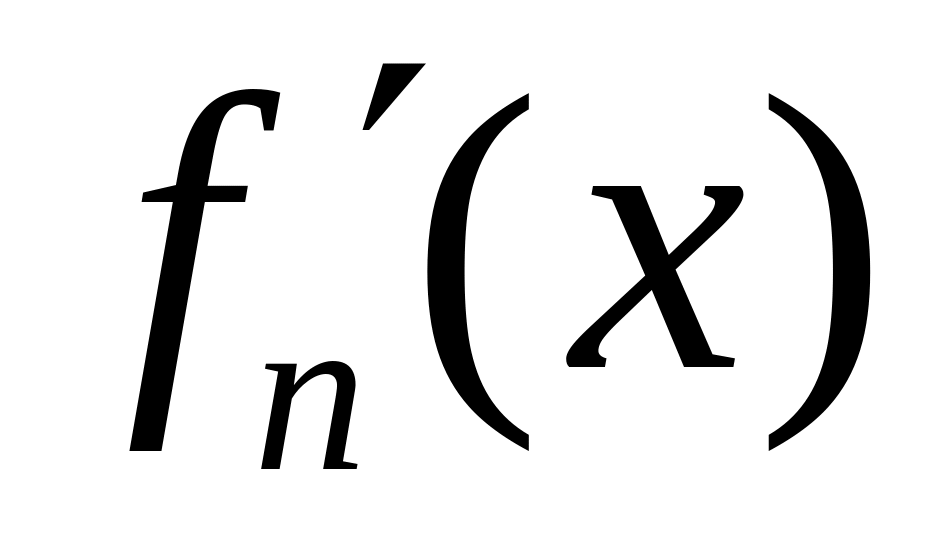3. ряд этих производных 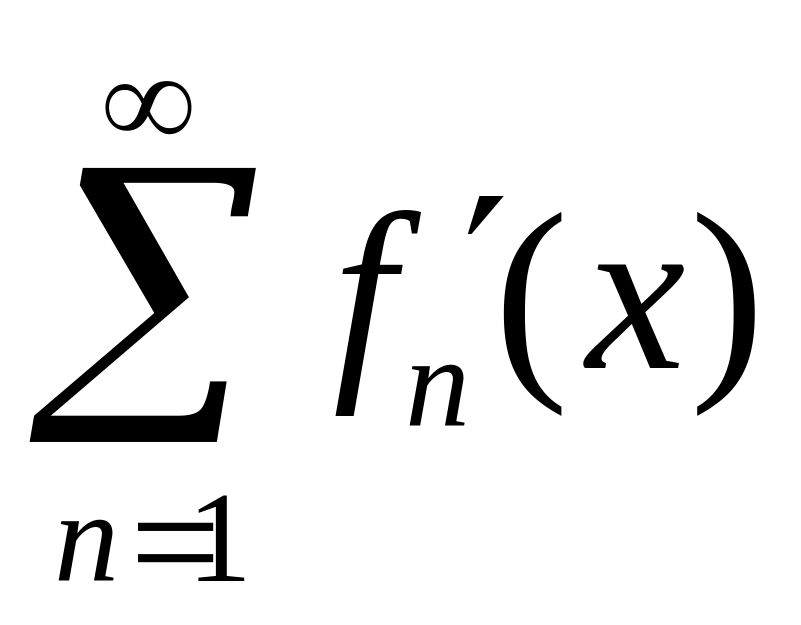сходится равномерно;

то данный функциональный ряд можно почленно дифференцировать в каждой точке упомянутого промежутка: .
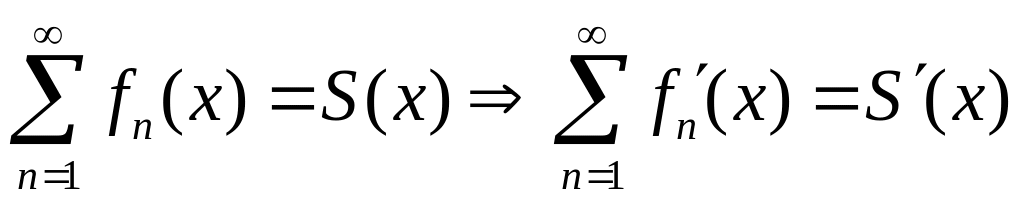
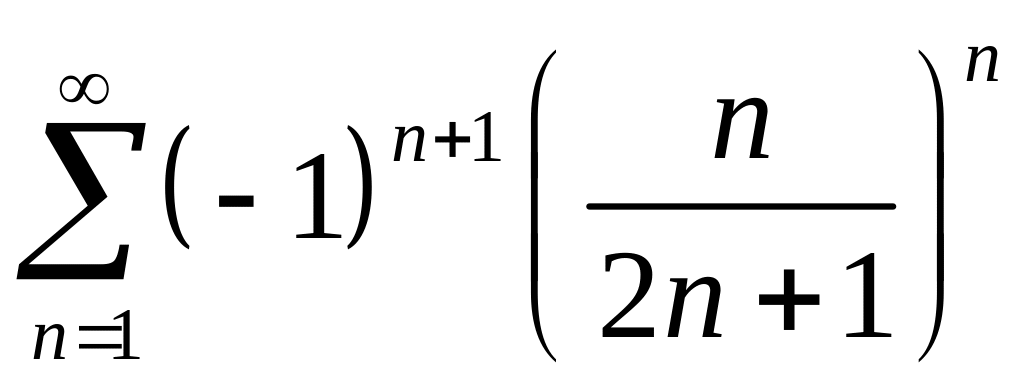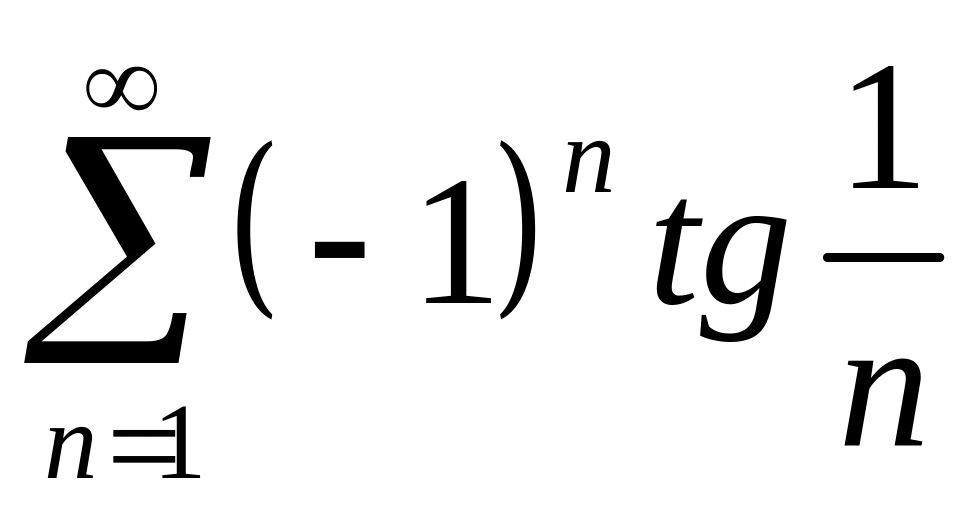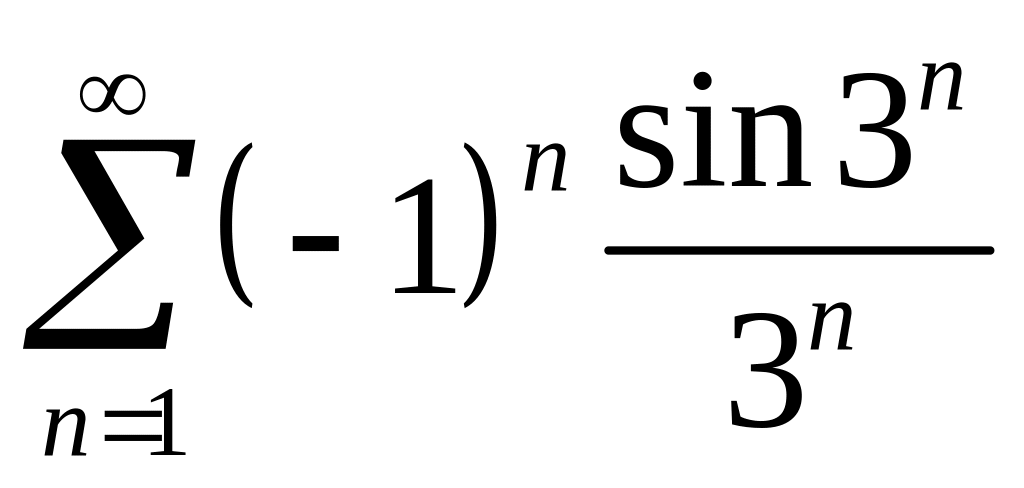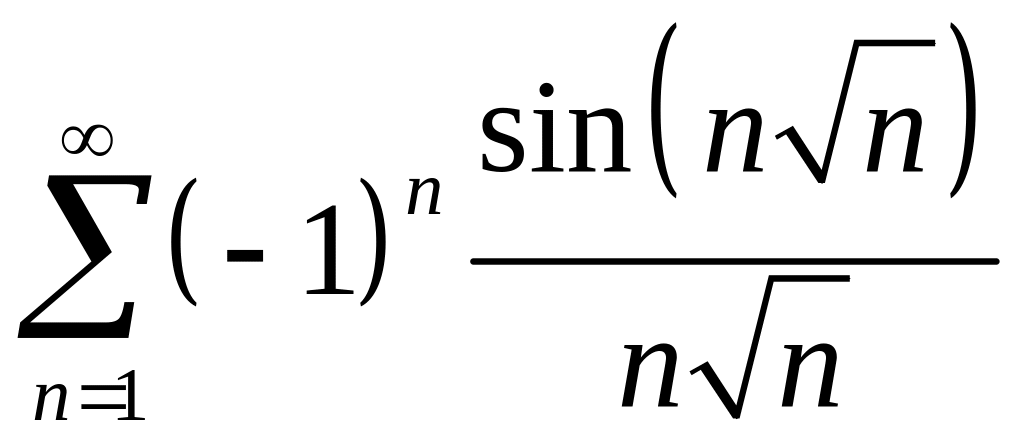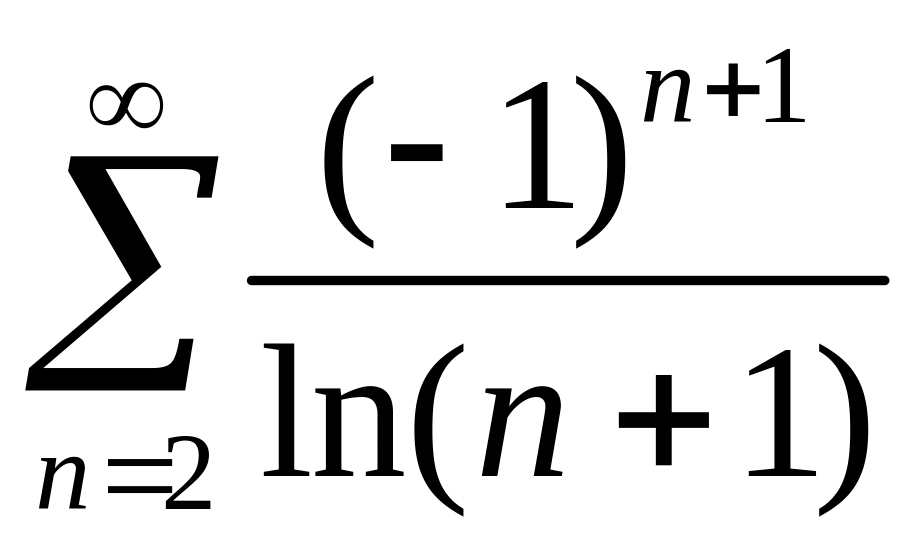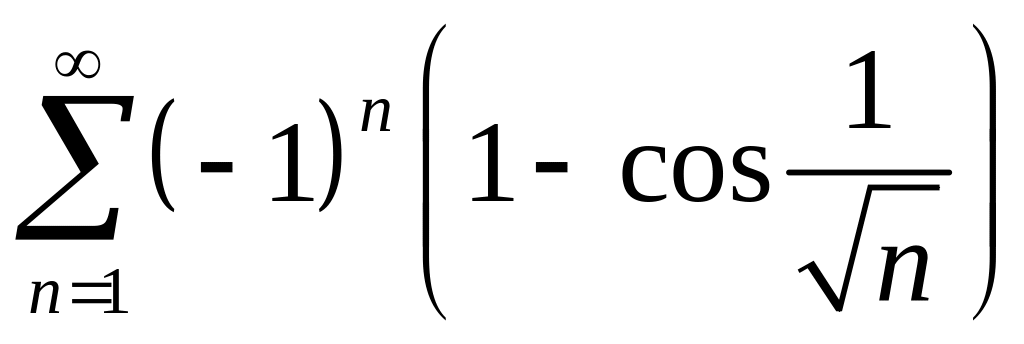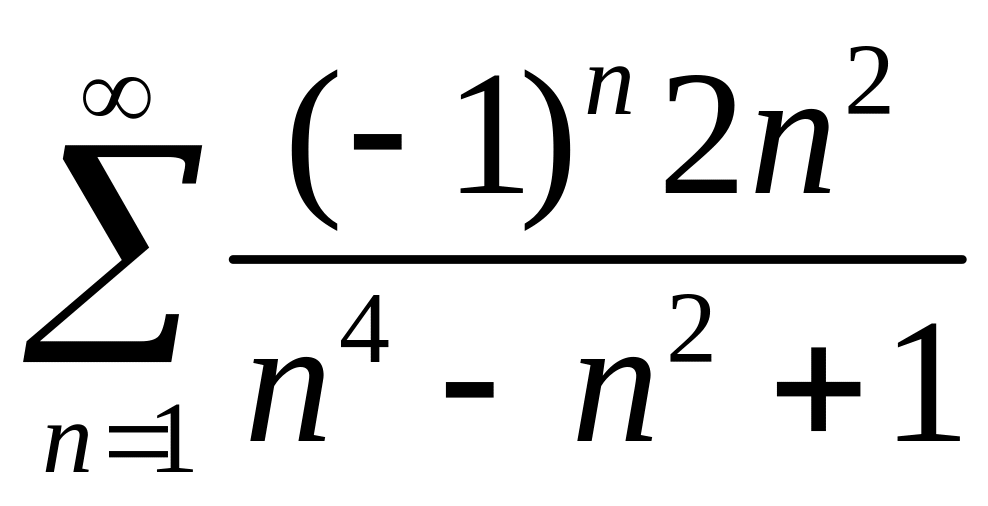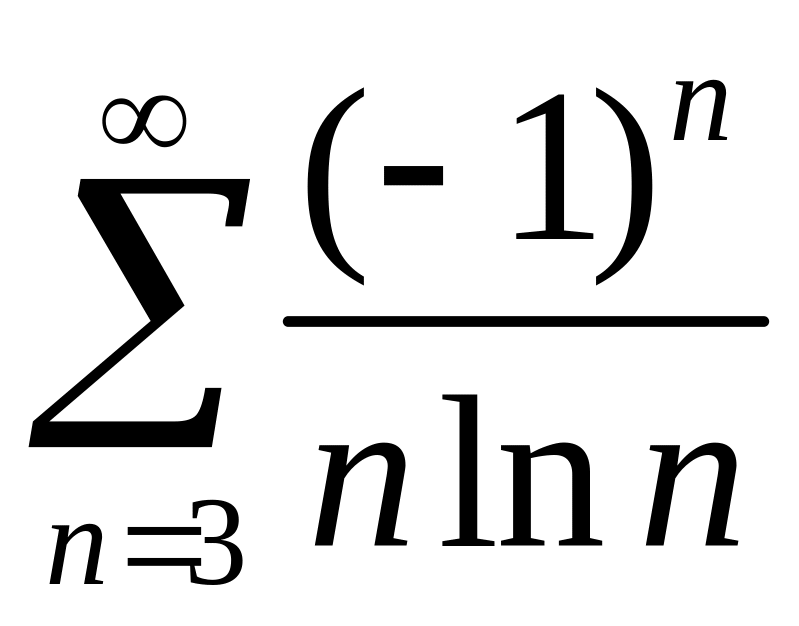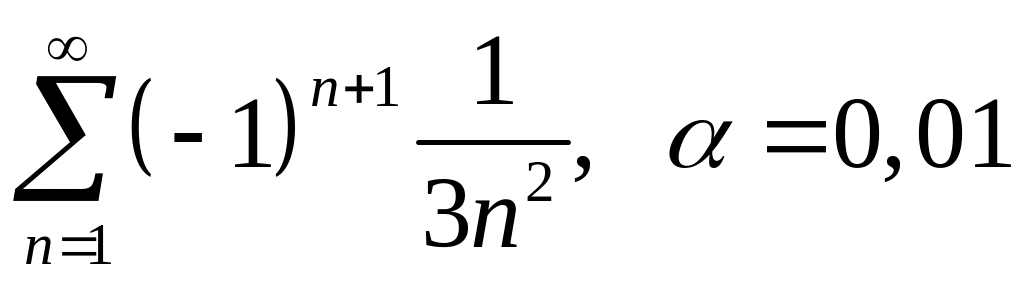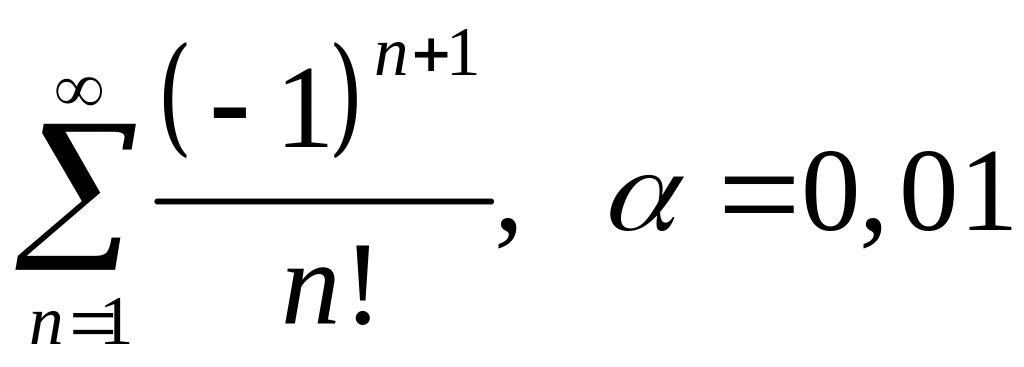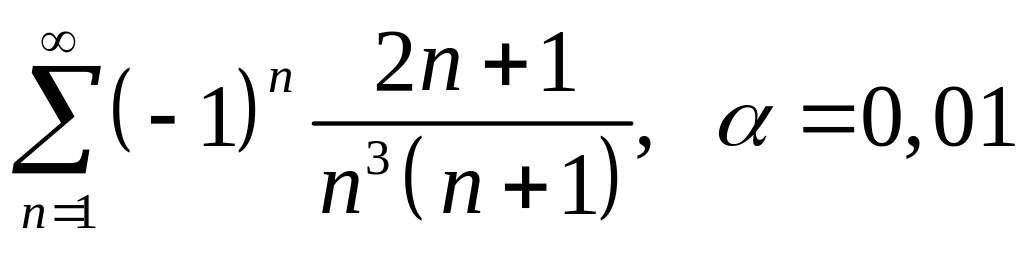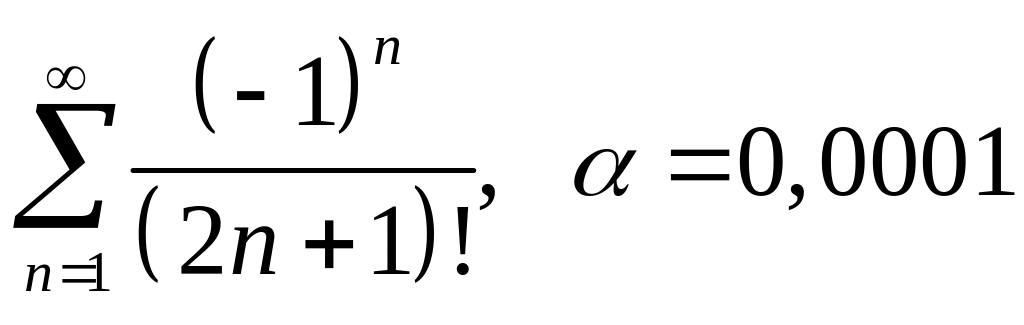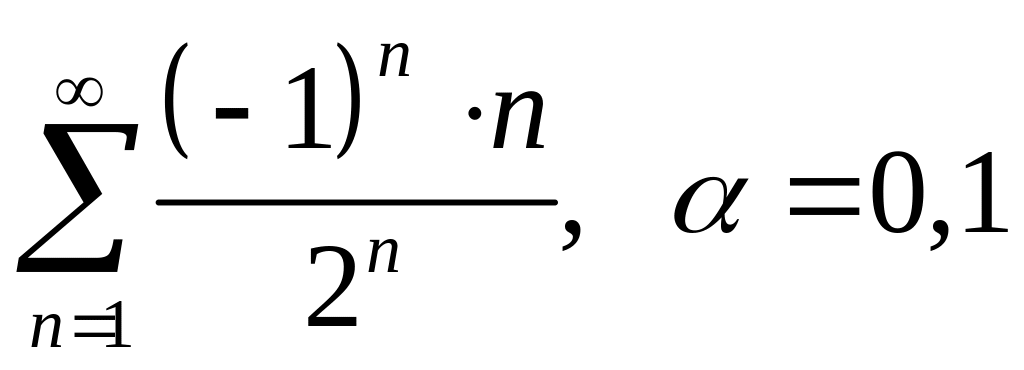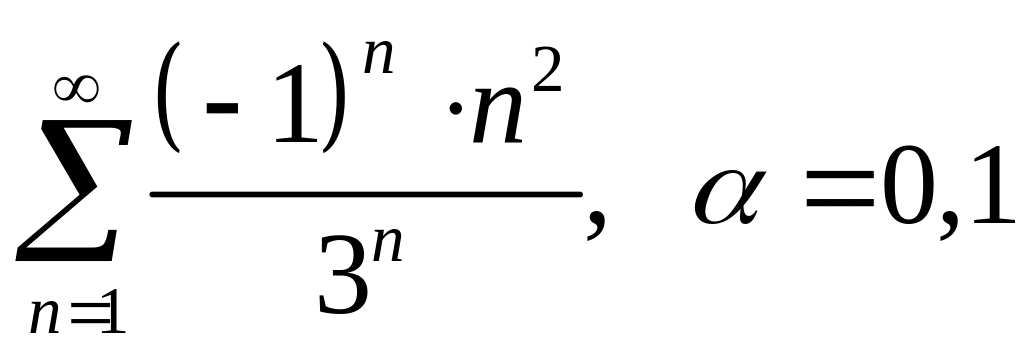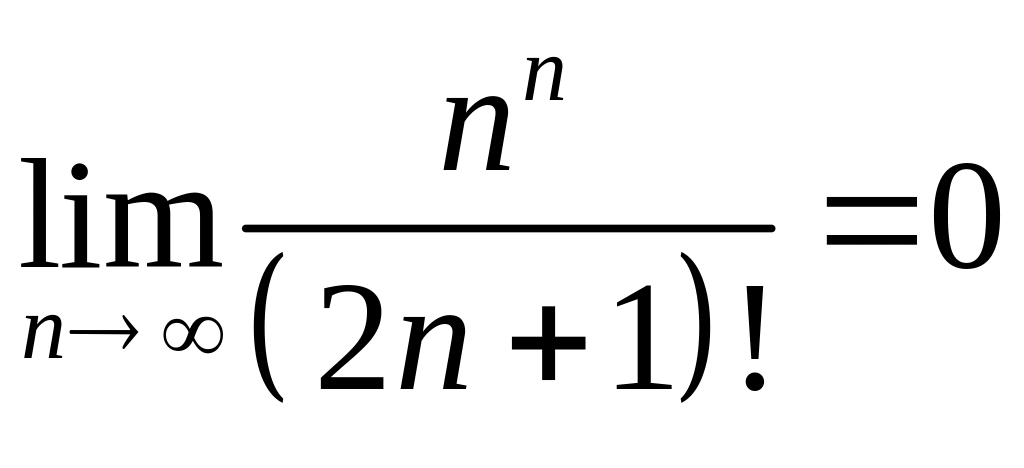
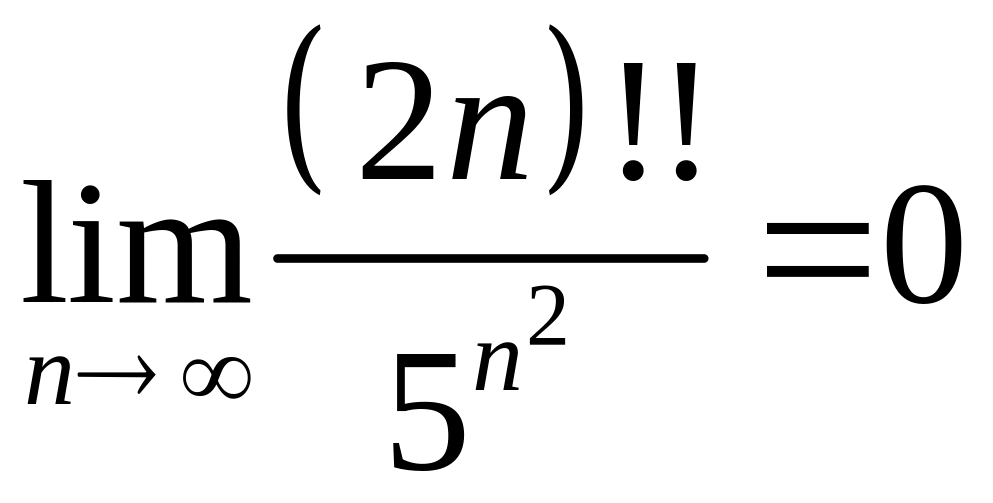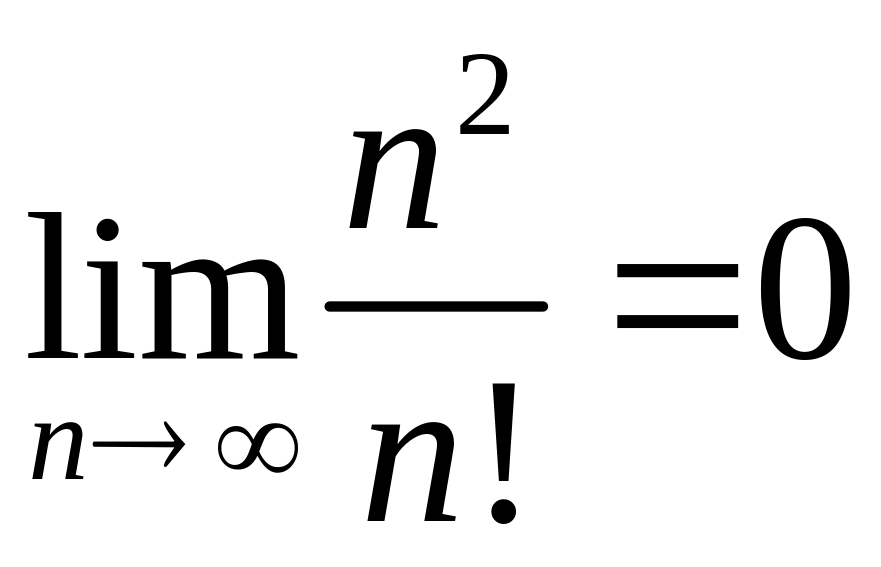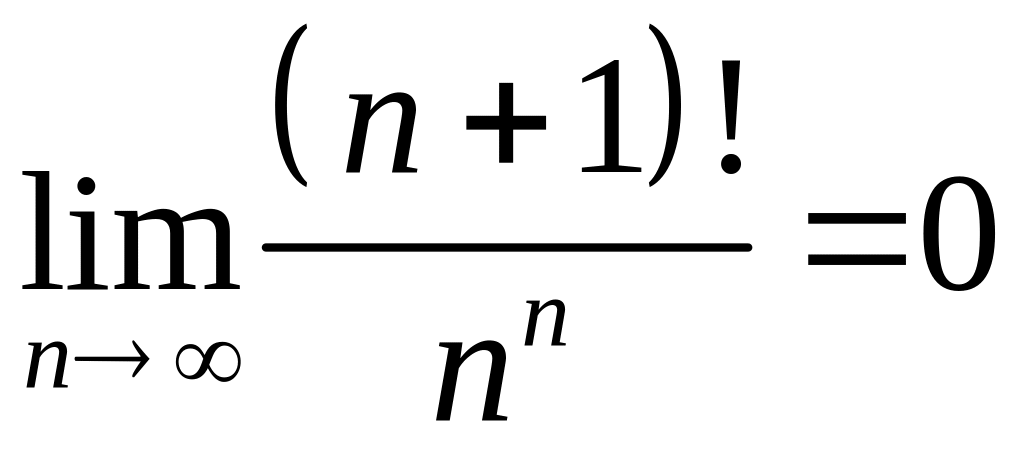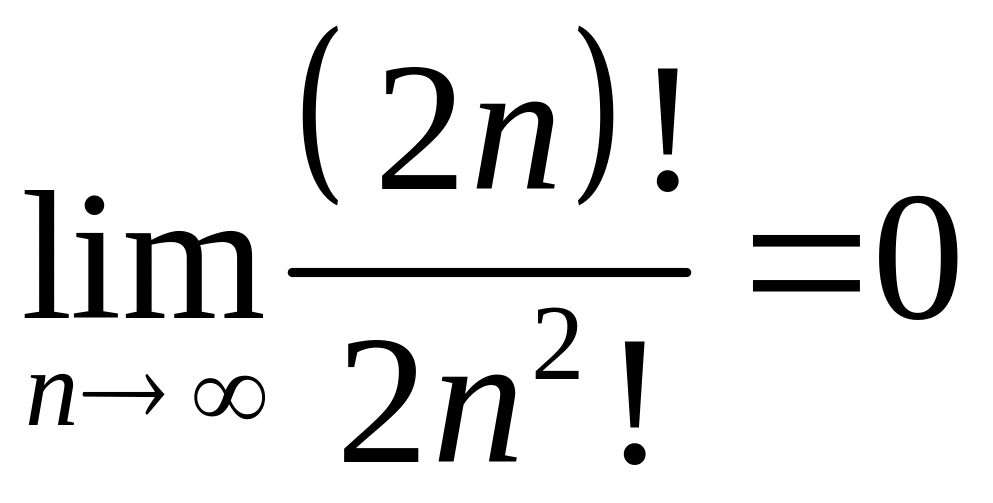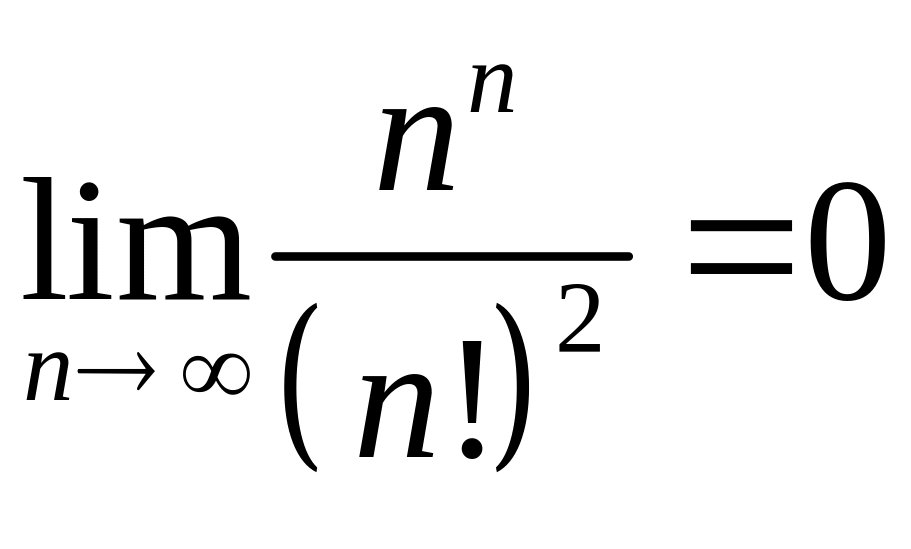