
- •10. Числовые и функциональные ряды
- •10.1. Числовой ряд. Основные понятия. Знакоположительные ряды Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •10.2. Знакочередующиеся ряды Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •10. 3. Функциональные ряды Краткие теоретические сведения
- •Примеры решения типовых задач
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •10.5. Разложение функций в ряды Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
- •10.6.Приложения в экономике теории рядов Краткие теоретические сведения
- •Примеры решения типовых задач
- •Задания для самостоятельной работы
10. Числовые и функциональные ряды
10.1. Числовой ряд. Основные понятия. Знакоположительные ряды Краткие теоретические сведения
Пусть
имеется числовая последовательность
![]() .
Составим выражение
.
Составим выражение
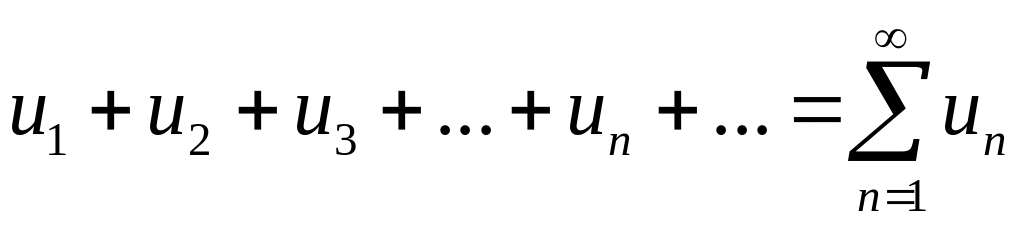 ,
которое называют числовым
рядом, а
числа
–
членами ряда; n-й
член ряда называется так же общим
членом ряда.
,
которое называют числовым
рядом, а
числа
–
членами ряда; n-й
член ряда называется так же общим
членом ряда.
Определение
1.
Сумма первых
n
членов ряда называется n-й
частичной суммой
ряда и обозначается
![]() :
:
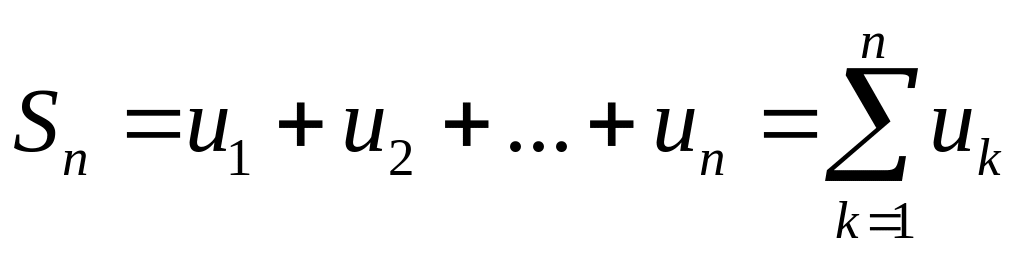 .
.
Определение
2. Суммой
ряда называется предел
последовательности частичных сумм
![]() ,
если он существует и конечен. В этом
случае то ряд называют сходящимся,
в противном случае – расходящимся.
,
если он существует и конечен. В этом
случае то ряд называют сходящимся,
в противном случае – расходящимся.
Определение
3.
Ряд
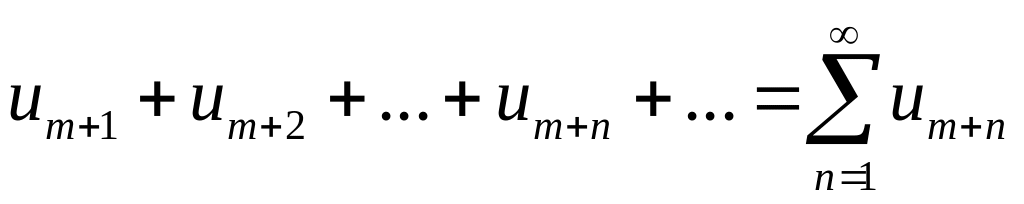 ,
полученный из ряда
отбрасыванием первых его m
членов называется m-м
остатком ряда.
,
полученный из ряда
отбрасыванием первых его m
членов называется m-м
остатком ряда.
Если
сумму остатка сходящегося ряда обозначить
через
![]() ,
то, очевидно,
,
то, очевидно,
![]() .
.
Справедливы следующие теоремы:
Теорема 1. Отбрасывание ряда, или присоединение к ряду любого конечного числа начальных членов не меняет его сходимости или расходимости.
Теорема
2. Если ряд
![]() сходящийся, то
сходящийся, то
![]() .
.
Теорема
3. Если члены
ряда
,
имеющего сумму S,
умножить на число
![]() ,
то полученный ряд
,
то полученный ряд
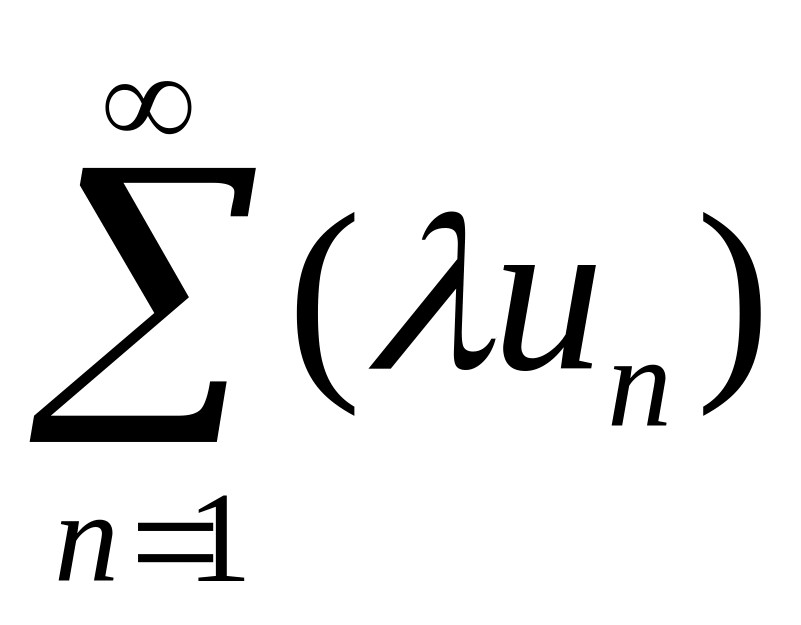 будет также сходящимся, а число
будет также сходящимся, а число
![]() –
его суммой.
–
его суммой.
Теорема
4. Умножение
членов расходящегося ряда на число
![]() не нарушит его расходимости.
не нарушит его расходимости.
Теорема
5 (необходимый признак сходимости).
Если ряд
сходится, то предел последовательности
его членов равен 0:
![]() .
.
Отсюда
следует, что если
![]() ,
то ряд расходится.
,
то ряд расходится.
Теорема
6 (Критерий Коши).
Для того, чтобы ряд
сходился, необходимо и достаточно, чтобы
для всякого
![]() существовало число
существовало число
![]() (зависящее только от
(зависящее только от
![]() )
такое, что для всех
)
такое, что для всех
![]() и любого натурального k
было справедливо неравенство
и любого натурального k
было справедливо неравенство
![]() .
.
Если все члены ряда положительные, то ряд называют знакоположительным.
Приведем основные признаки сходимости знакоположительных рядов.
Признаки сравнения. Пусть имеем 2 знакоположительных ряда:
(1);
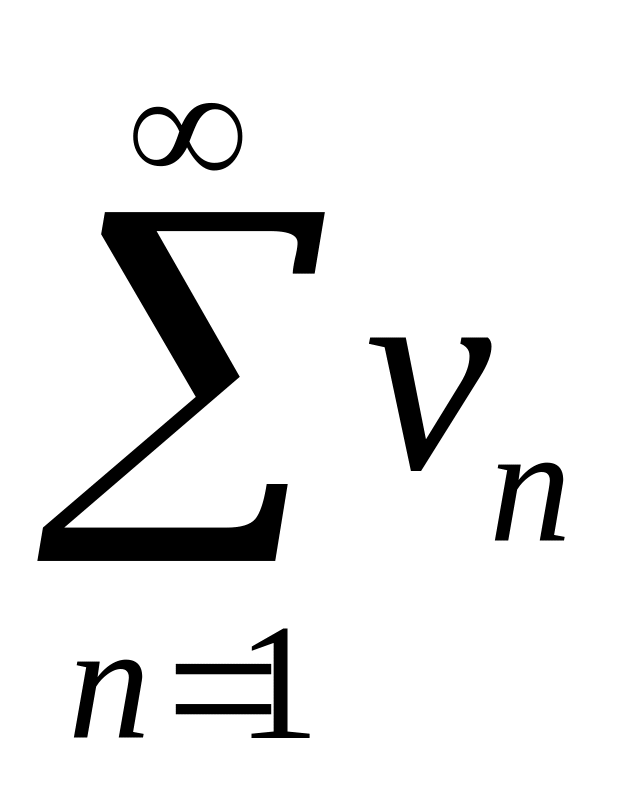 (2).
(2).
1.
Если для всех членов рядов (1) и (2), начиная
с некоторого номера, выполняется
равенство
![]() ,
то из сходимости ряда (2) следует сходимость
ряда (1); из расходимости ряда (1) следует
расходимость ряда (2).
,
то из сходимости ряда (2) следует сходимость
ряда (1); из расходимости ряда (1) следует
расходимость ряда (2).
2.
Если существует конечный предел
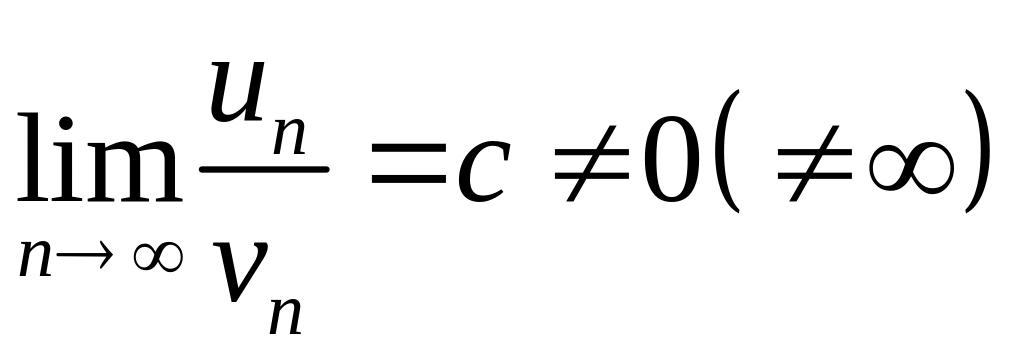 ,
то оба ряда (1) и (2) сходятся или расходятся
одновременно.
,
то оба ряда (1) и (2) сходятся или расходятся
одновременно.
Замечание 1. Сравнение исследуемых рядов производится обычно со следующими рядами:
а)
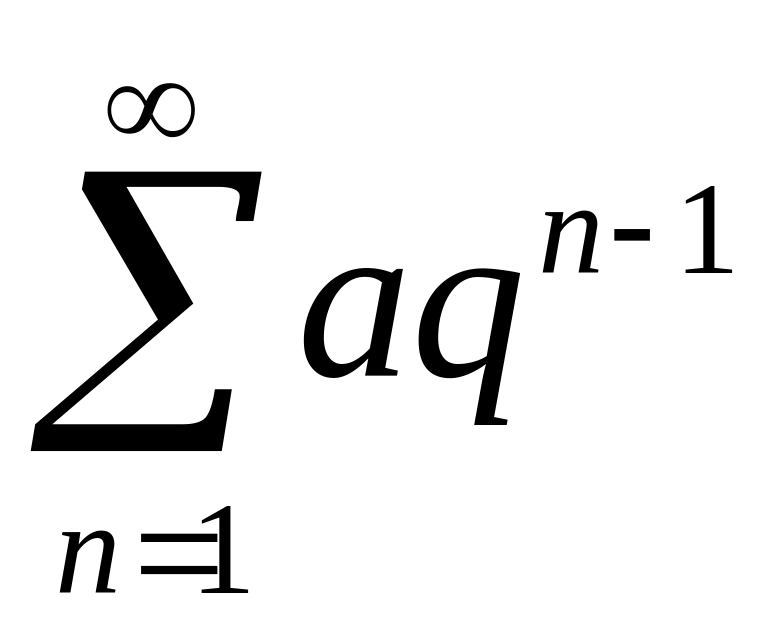 ,
,
![]() (геометрическая
прогрессия, сходящаяся при
(геометрическая
прогрессия, сходящаяся при
![]() и расходящаяся при
и расходящаяся при
![]() );
);
б)
![]() (расходящийся гармонический ряд);
(расходящийся гармонический ряд);
в)
![]() (обобщенный
гармонический ряд, сходящийся при
(обобщенный
гармонический ряд, сходящийся при
![]() и расходящийся при
и расходящийся при
![]() ).
).
Замечание
2. Если, в
частности, общие члены сравниваемых
рядов эквиваленты при
![]() (
(![]() ),
то оба ряда (в смысле сходимости) ведут
себя одинаково.
),
то оба ряда (в смысле сходимости) ведут
себя одинаково.
Признак
Даламбера.
Если
![]() –
знакоположительный ряд и существует
конечный или бесконечный предел
–
знакоположительный ряд и существует
конечный или бесконечный предел
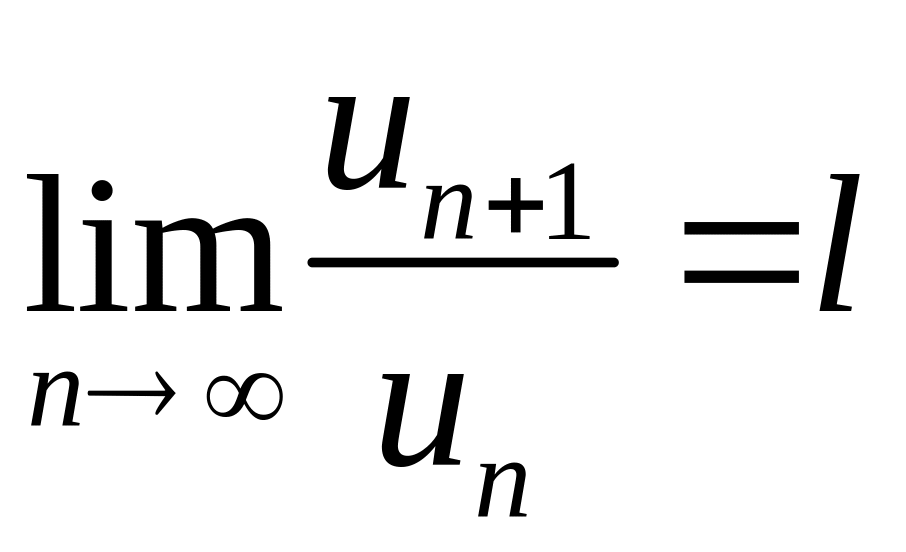 ,
то при
,
то при
![]() ряд
сходится;
при
ряд
сходится;
при
![]() ряд
расходится; при
ряд
расходится; при
![]() вопрос остается открытым.
вопрос остается открытым.
Признак
Коши.
Если
–
знакоположительный ряд и существует
конечный или бесконечный предел
![]() ,
то при
,
то при
![]() ряд
сходится; при
ряд
сходится; при
![]() ряд
расходится; при
ряд
расходится; при
![]() вопрос остается открытым.
вопрос остается открытым.
Признак
Раабе.
Если
–
знакоположительный ряд и существует
конечный или бесконечный предел
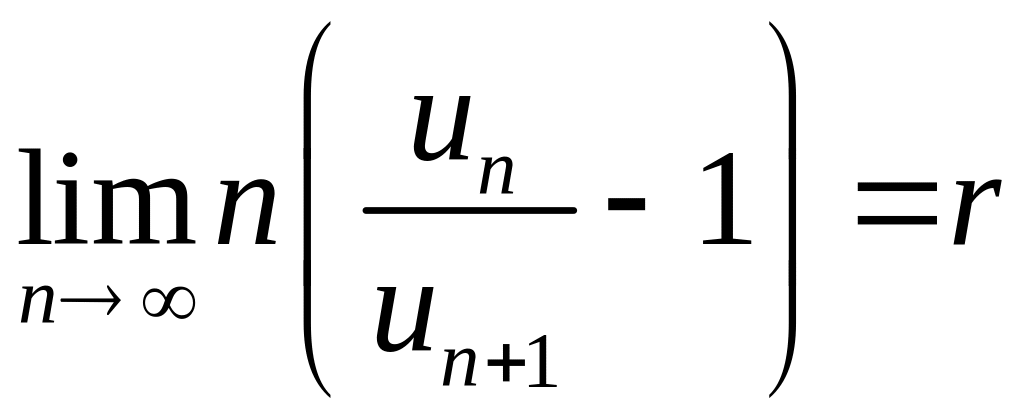 ,
то при
,
то при
![]() ряд
сходится; при
ряд
сходится; при
![]() ряд
расходится; при
ряд
расходится; при
![]() вопрос остается открытым, т.е. о сходимости
или расходимости ряда ничего сказать
нельзя, нужны дополнительные исследования.
вопрос остается открытым, т.е. о сходимости
или расходимости ряда ничего сказать
нельзя, нужны дополнительные исследования.
Интегральный
признак.
Если функция
![]() непрерывна, неотрицательна и не возрастает
при
непрерывна, неотрицательна и не возрастает
при
![]() ,
то ряд
,
то ряд
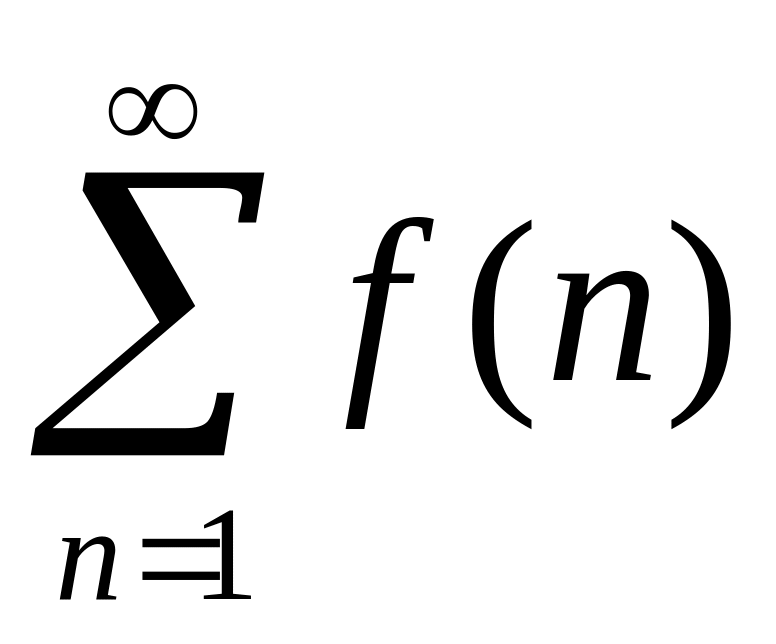 сходится или расходятся одновременно
с несобственным интегралом
сходится или расходятся одновременно
с несобственным интегралом
 .
.
Признак
Бертрана.
Если
–
знакоположительный ряд и существует
конечный
или бесконечный предел
 ,
то при
,
то при
![]() ряд сходится; при
ряд сходится; при
![]() ряд расходится; при
ряд расходится; при
![]() вопрос остается открытым.
вопрос остается открытым.
Замечание.
При оценке факториалов больших чисел
и вычислении пределов, содержащих
![]() часто бывает полезна формула Стирлинга
часто бывает полезна формула Стирлинга
![]() .
.
