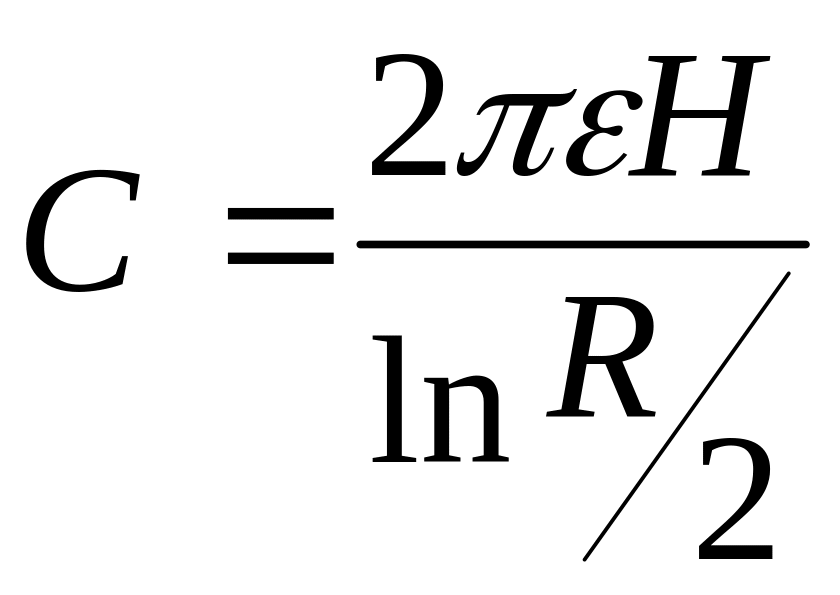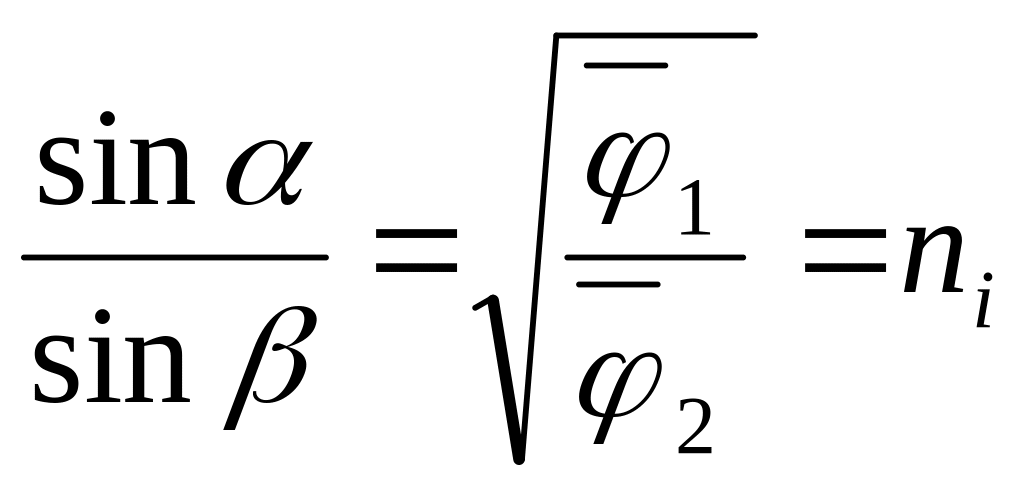Моделирование электростатических полей

В электролитической ванне.

(Описание к лабораторной работе)

Саратов - 2012

Электрическое моделирование.

Известно, что распределение потенциала электростатического поля в вакууме описывается уравнением Лапласа:

(1)

Эта математическая модель предполагает наличие зарядов только на поверхностях, определяющих конфигурацию системы электродов, создающих поле и отсутствие зарядов вне этих поверхностей.

Известно также, что в слое однородного проводящего вещества (электролита) распределение потенциала описывается также уравнением Лапласа. Это дает основание утверждать, что при подобных граничных условиях решение этого уравнения для вакуума и электролита также будут подобны. Каковы же критерии требуемого подобия? Для объема, не содержащего свободных зарядов в непроводящей среде справедливо соотношение

DivD = 0

(2)

Для объема проводника (электролита), не содержащего источников тока, справедливо похожее соотношение:

Div J = 0

(3)

Известно также, что D=E, j=E, a E=-grad.

С учетом этих соотношений выражений (2) и (3) можно переписать в виде:

div(-grad=0	(2’)
div(-grad=0	(3’)

Для однородных сред =Const и =Const, поэтому

- div grad = 0	(2’’)
-div grad = 0	(3’’)

Внеся константы под знаки дифференцирования и обозначив потенциал в непроводящей среде _н, а в проводящей _п получим:

(4)

Div grad (n) = 0	(4)
Div grad (n) = 0	(5)

Из сопоставления математических моделей (4) и (5) сразу вытекает первый критерий подобия:

n = n

(6)

Полученное равенство приводит к выводу, что одна и та же система электродов в непроводящей среде образует диэлектрическую ёмкость С, а в проводящей — проводимость G, связанных отношением

(7)

Другие критерии подобия рассмотрим на примере плоской (двумерной) задачи. Известно, что

Рассмотрим случай, когда

 = k,

x = M?l,

y = M?n.

(8)

Если k=_max, то  безразмерно, и его можно считать относительным потенциалом.

Из (8) видно, что для систем, геометрически подобных ( x и y изменим в M раз) распределение относительного потенциала неизменно. Поэтому вторым критерием подобия является геометрический масштаб, а третьим — масштаб изменения потенциалов на электродах.

Изложенное служит теоретическим основанием для реализации принципа электролитической аналогии при физическом моделировании задач, описываемых уравнением Лапласа.

Ниже рассматриваются примеры использования данного принципа для решения ряда прикладных задач.

Моделирование физических полей в электролитической ванне

Известные физики XIX века Г.Кирхгоф, М.Фарадей, Г.Гельмгольц, Д.Максвелл установили математические аналогии электрических, магнитных, тепловых и гидродинамических полей. В таблице приведены уравнения, описывающие физические поля в однородных средах.

Из таблицы видно, что математически задачи определения тех или иных характеристик полей совершенно аналогичны и сводятся к решению краевых задач. Метод электроаналогий дает при просторе моделирования достаточную точность и оперативность решения.

Наиболее распространенным техническим воплощением метода электроаналогий является электролитическая ванна. Типичное оборудование для электролитической ванны приведено на рис… Принципиальная схема установки приведена на рис…

С помощью описанной установки можно решить либо плоские (двумерные) либо осесиммитричные трехмерные задачи.

В первом случае в ванне с горизонтальным дном создается плоско-параллельный слой проводящей жидкости (например, водопроводной воды). Граничные условия задаются подачей относительных потенциалов с резистивных делителей на электроды, повторяющие в выбранном масштабе форму поверхности электродов оригиналов. Перемещая с помощью каретки зонд, находят точки на поверхности электролита, в которых относительный потенциал имеет заданное также с помощью резистивного делителя значение. Поскольку сравнение потенциала зонда с опорным потенциалом производится с помощью осциллографа, цепь зонда является без токовой, и он не вносит искажения в картину поля. Найденные точки отмечаются на бумаге и соединяются плавной линией (изолиния). Набор изолиний плюс местоположение электродов дают картину поля в модели, пригодной для последующей обработки. На рис.. показаны результаты моделирования поля электростатической системы фокусировки пучка электронов в электронном вакуумном приборе.

Если требуется найти распределение поля в осесимметричных трехмерных моделях, модель напоминает ломтик круглого хлеба (рис...)

В рассмотренном случае дно электролитической ванны устанавливают под углом 10-20 градусов к горизонту. Модель электродов проектирует диаметральным сечением оригинала и масштабированием. Ось симметрии совмещают с линией нулевой глубины электролита.

Следует отметить, что при любом виде моделирования в электролитической ванне плоскости по которым “вырезается ломтик” модели должны располагаться вдоль линий тока (потока). Это гарантирует адекватность распределения поля в этом “ломтике” модели с распределением в полной модели.

Еще раз подчеркнем, что все сказанное относится к моделированию полей в пространстве, в котором отсутствуют источники полей и поля стационарны.

Моделирование полей в пространстве, содержащем источники поля.

Известно, что если в задачах, подобных ранее рассмотренным, требуется учесть присутствие в заданных областях источников поля, применяется уравнение Пуассона:



(9)

Вследствие того, что в потенциальных полях действует принцип суперпозиции, поле  можно представить в виде суммы полей ₀ и _n:

=0+n………….

(10)

где ₀  поле той же системы электронов, но без источников поля,

_n  поле, создаваемое источниками поля.

Тогда, в силу сказанного

=0	(11)
n=	(12)

Моделирование для уравнения (11) уже рассмотрено. Моделирование картины поля, создаваемого свободными зарядами в середине 50-х годов предложено производить путём введения расчётных токов, вводимых в электролит через специальные электроды в дне ванны. Суммируясь с токами в модели к уравнению (11), они создают распределение потенциала, описываемое уравнением (10).

Расчёт величин тока проводится …………………………

Примеры использования электролитической ванны для решения прикладных задач.

1. Расчетно-эксперементальный метод определения электрической ёмкости для электродов сложной формы.

В практике разработчиков элементной базы для радиоэлектронной аппаратуры или емкостных преобразователей (датчиков) различного назначения требуется определить величину электрической емкости между электродами сложной формы. Чаще всего она сопоставляет величину порядка десятка или сотен микрофарад. Теоретический расчёт в этом случае даёт значительную погрешность, а непосредственное измерение на макете не позволяет исключить влияние соединительных проводников и соседних деталей. Если же воспроизвести модель этих электродов в электролитической ванне и измерить проводимость слоя электролита между электронами G , то, в соответствии с (7) можно пересчитать её в ёмкость модели С:

(13)

Нетрудно показать, что при геометрическом масштабе M, искомая ёмкость С_x будет в M раз меньше:

(14)

На практике достаточно сложно обеспечить постоянство удельной проводимости электролита, на которую влияют температура окружающей среды и процессы химического взаимодействия его с материалом электродов, и ряд других факторов.

Поэтому проще сравнить величину G для исследуемой модели с проводимостью промежутка для электродов правильной формы, для которых величина ёмкости известна. Например, можно использовать модель цилиндрического конденсатора. В этом случае также (7)

(15)

Поделив, правые и левые части равенств (13) и (15), получим, что

(16)

Отношение G_m/G₀ измеряется опытным путём в ванне, а G₀  рассчитывается по формуле для цилиндрического конденсатора. Поэтому такой метод называется расчётно-эксперементальным. В данном случае не требуется знать величины  и , что значительно упрощает задачу.

2. Метод электроаналогий для расчёта электрической ёмкости.

Выражение (7) можно использовать для аналитического исследования поведения ёмкости конденсатора, например, при деформации образующих его электродов. Рассмотрим данный метод снова на примере цилиндрического конденсатора (рис…).

“Вырежем” из слоя электролита сектор с углом dx. Отметим, что проводимость всей модели равна сумме проводимостей секторов dG:

(17)

Поскольку линии (трубки) тока в данной модели расширяются, проще рассчитать сначала обратную величину проводимости, т.е. сопротивление.

Выделим в рассматриваемом секторе слой толщиной dx на радиусе x. Известно, что у проводника:

(18)

Где l  длина проводника (в нашем случае dx)

S  площадь поперечного сечения (в нашем случае X*dx*H)

H  высота электродов в модели.

Тогда

(19)

И сопротивление всего сектора

(20)

Следовательно, проводимость сектора будет равна обратной величине :

(21)

Теперь остаётся просуммировать частичные проводимости от каждого сектора d:

(22)

Используя (13) получим окончательно

(22а)

Что совпадает с выражением, полученным традиционным способом.

3. Построение траектории заряженной частицы, влетающей в область электростатического поля.

При проектировании электронно-лучевых приборов требуется обеспечить движение электронов через заданные зоны прибора. Раздел электроники, изучающий эти вопросы, назвали электронной оптикой. Название это удачно отражает подходы и методы исследования.

В однородных средах потенциал электростатического поля не может меняться скачком. Но если известно распределение потенциала в некоторой области, можно условно разделить эту область на зоны с условно-постоянным потенциалом, причём границами зон будут эквипотенциалами.

………..

Рассмотрим траекторию электрона при переходе его в соседнюю зону.

Пусть электрон движется в зоне I под углом  к эквипотенциалам.

Известно, что его кинетическая энергия равна работе сил поля, т.е.

(23)

Если V не слишком велико (не нужно учитывать релятивистские эффекты),

(24)

Аналогично для зоны II

(25)

В рассмотренном случае вектор скорости имеет нормальную (вдоль вектора n) и тангенциальную (вдоль касательной) составляющие:

Vn1 = V1·cos α; VT1 = V1?sin α	(26)
Vn2 = V2·cos β; VT2 = V2?sin β	(27)

Электростатическое поле действует на заряженную частицу только в направлении градиента потенциала (т.е. нормали к границе раздела). Следовательно, тангенциальная составляющая скорости не изменится, или

V_T1 = V_T2.

Учтем при этом значения V_T1 и V_T2 из (26) и (27):

V1?sin α = V2?sin β

(28)

С учетом (24) и (25) можно окончательно записать, что

(29)

Выражение (29) напоминает закон преломления в геометрической оптике. Поэтому и построение траектории заряженной частицы напоминает построение хода лучей в неоднородной (слоистой) среде. Для облегчения этой процедуры Граффундером была создана специальная комбинированная линейка, рассчитанная на работу с картиной эквипотенциальных линий, снятых через 0.1 относительно потенциала (т.е. 0; 0.1; 0.2; … 0.9 и 1.0). Описание линейки Граффундера и правила пользования ей приведено в приложении.