§ 6. Головне значення (за Коші) розбіжних невласних інтегралів

Нехай визначена на і 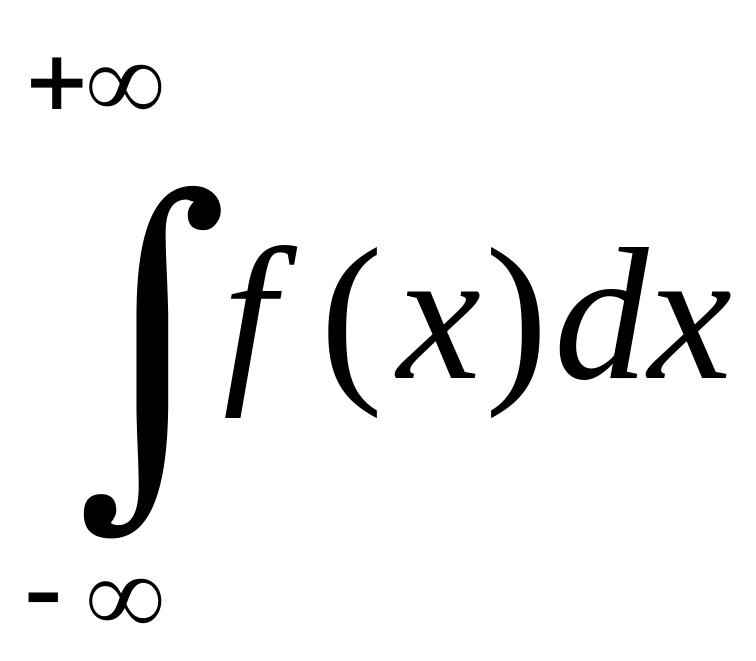розбігається.

Означення 1. Якщо функція інтегруєма за Ріманом на будь-якому відрізку із і

,

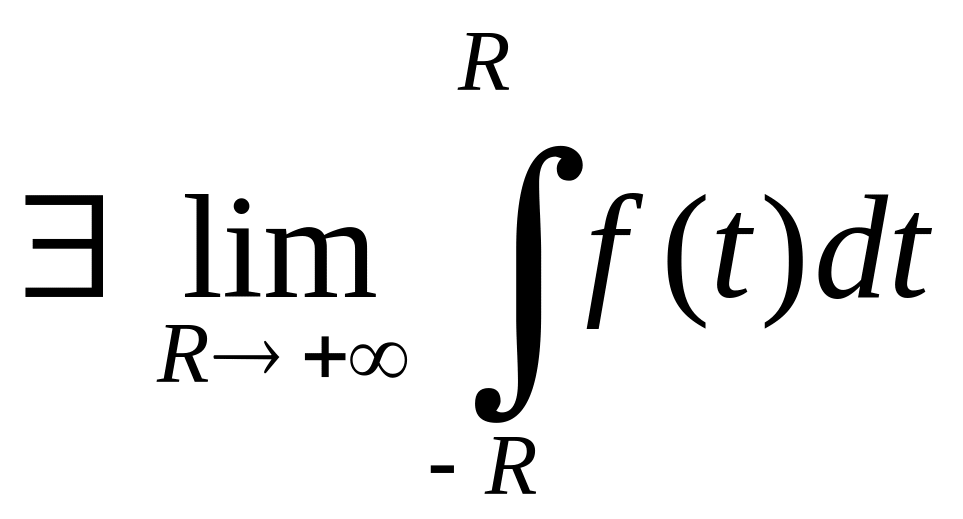то вказану границю називають головним значенням (за Коші) розбіжного інтеграла 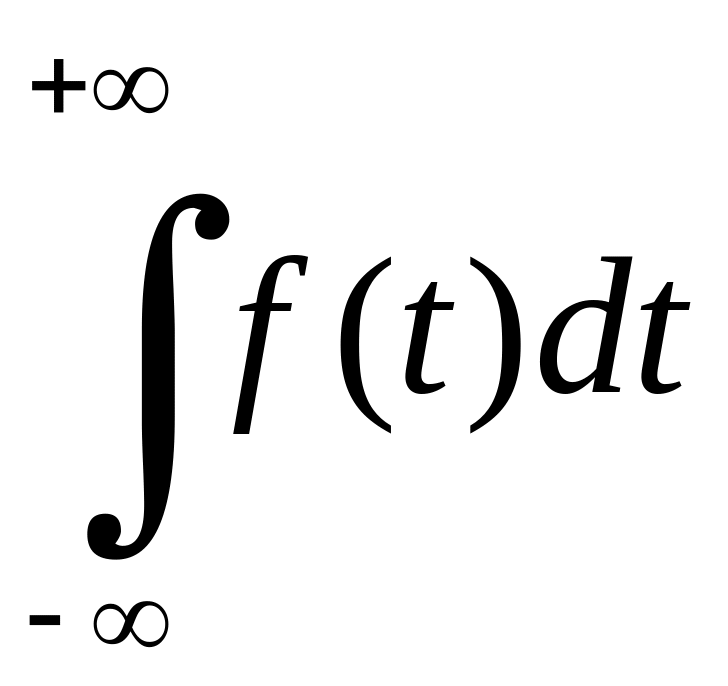і позначають

.

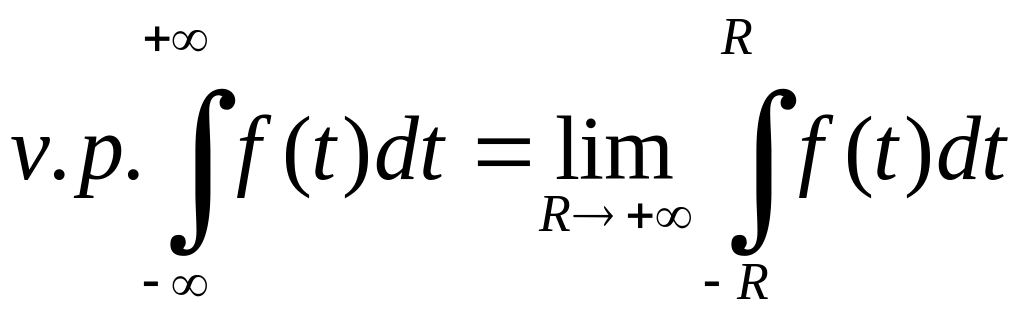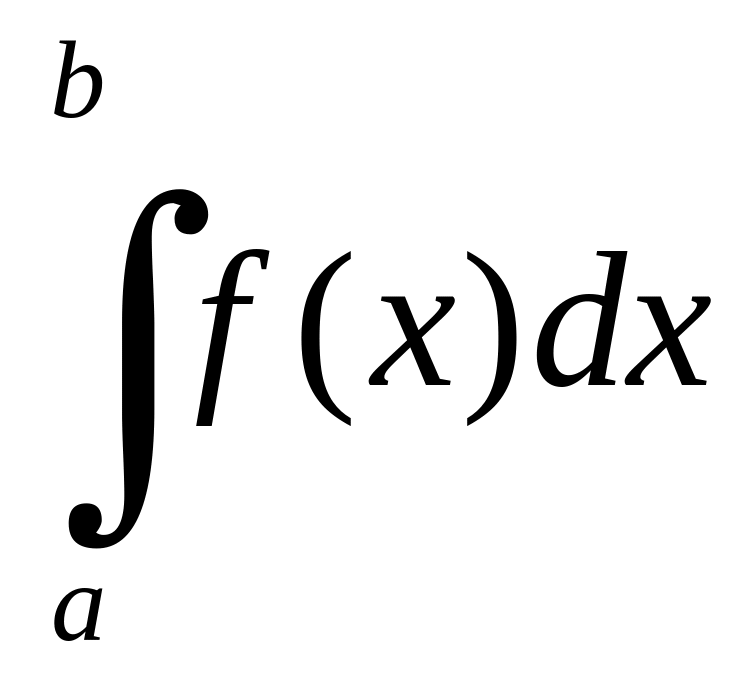Означення 2. Якщо визначена на множині , , і інтеграл розбігається, то

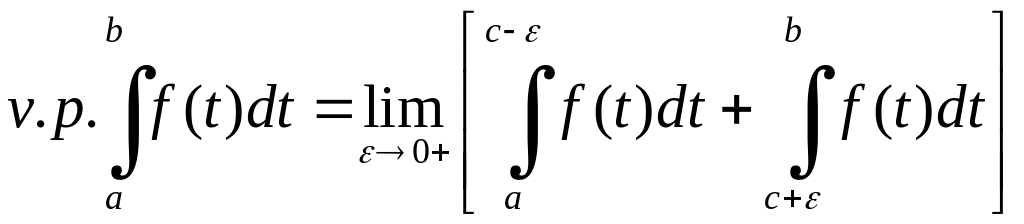
за умовою, що існують 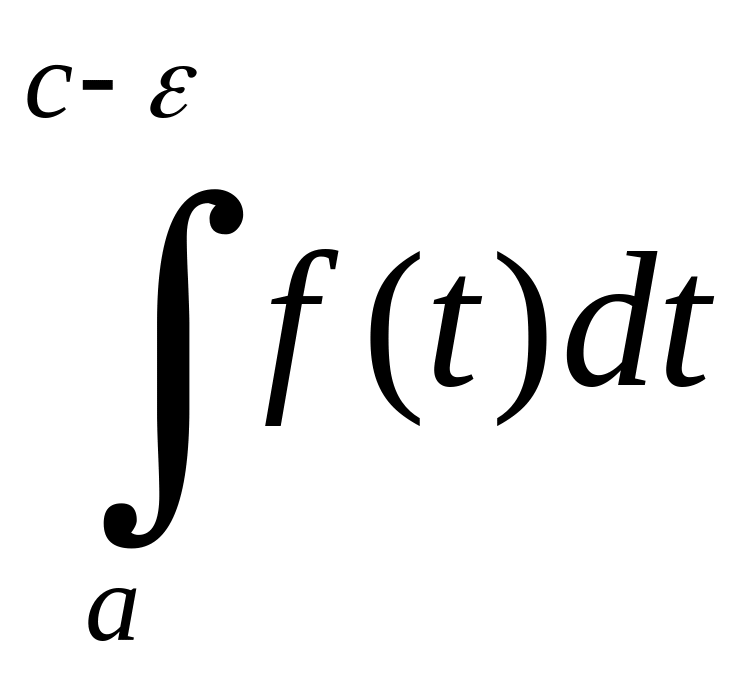і 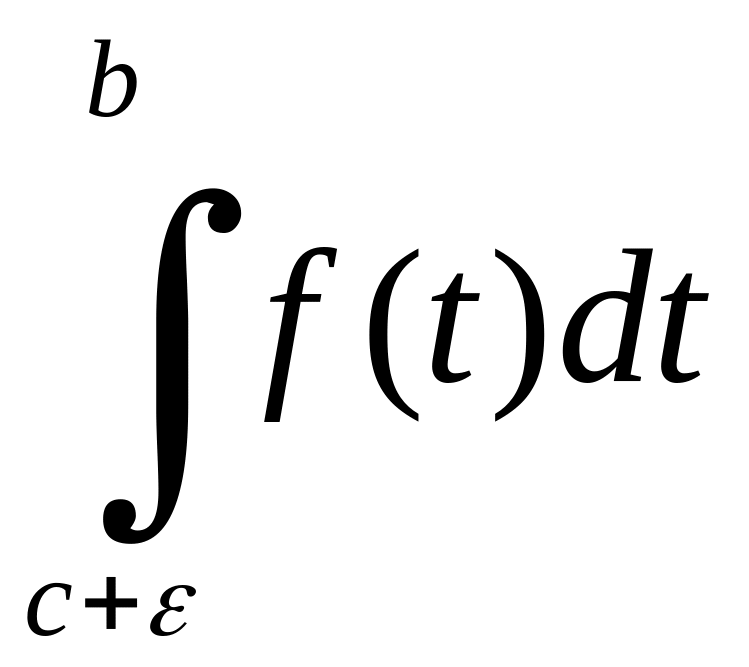при достатньо малому .

Приклад 6.1. Розглянемо інтеграл

.

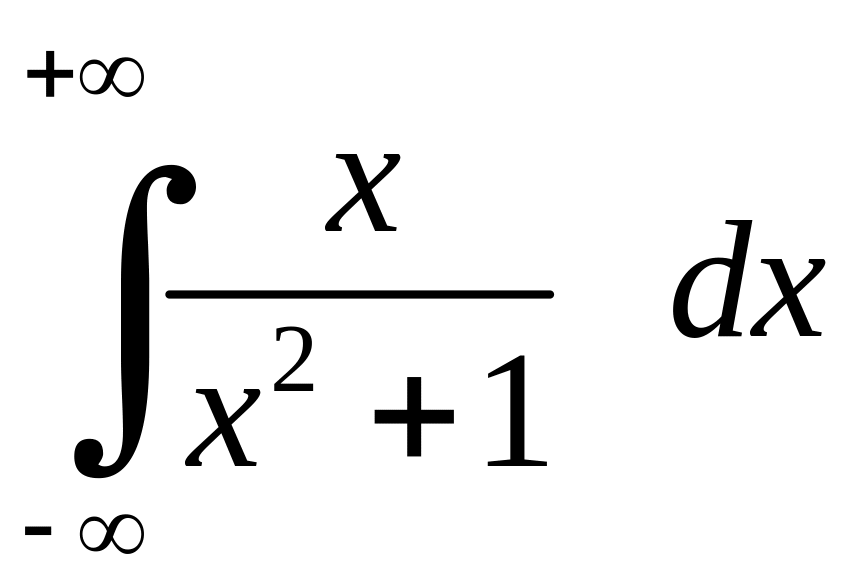Розв'язання. Зрозуміло, що інтеграл розбігається, оскільки

,

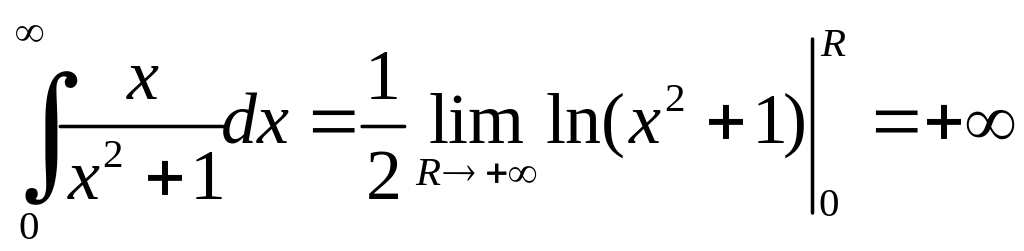але

,

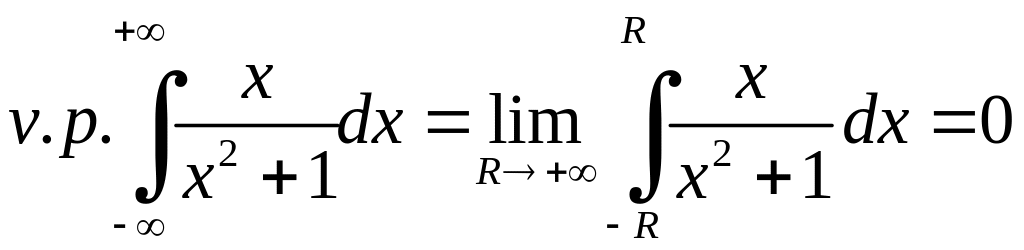тому що при будь-якому інтеграл від непарної функції на симетричному проміжку дорівнює 0.

Зрозуміло, що

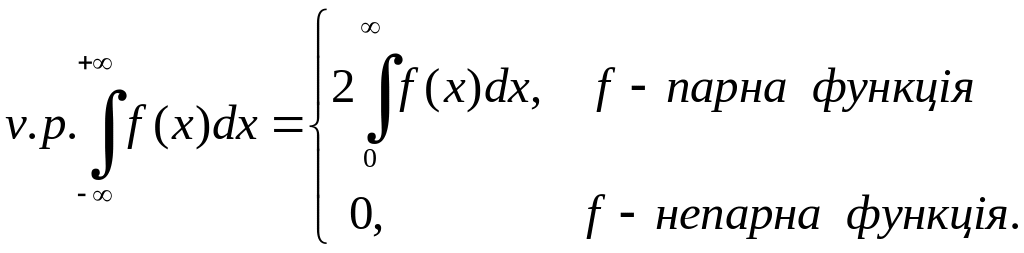
Приведемо декілька прикладів на дослідження невласних інтегралів. У випадку, коли вони збігаються, обчислимо їх.

Приклад 6.2. Обчислити інтеграл

.

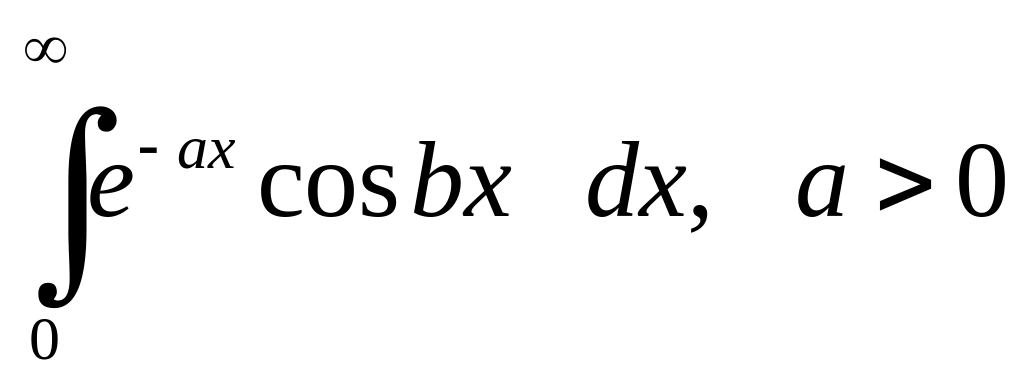Розв'язання. За умови Діріхле, де , , цей інтеграл збігається (і навіть абсолютно), а тому за означенням

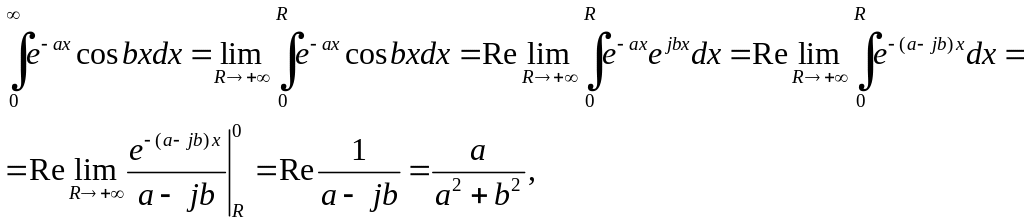
тому що , , і коли , то , а тому і .

Отже,

, .

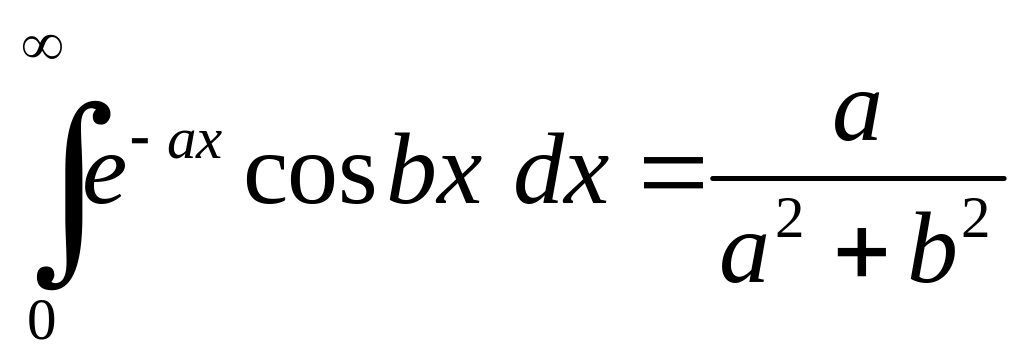Аналогічно

, .

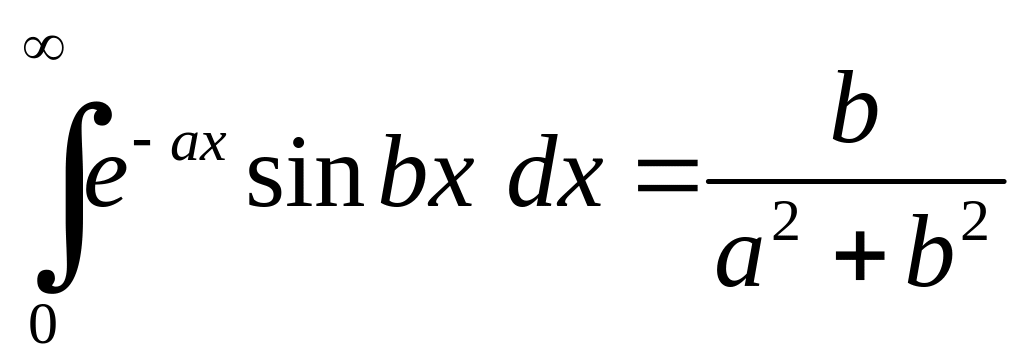Приклад 6.3. Нехай , параметр. Функція додатна, нескінченно мала, коли , того ж порядку, що і . Оскільки збігається, то з урахуванням важливого зауваження, збігається і 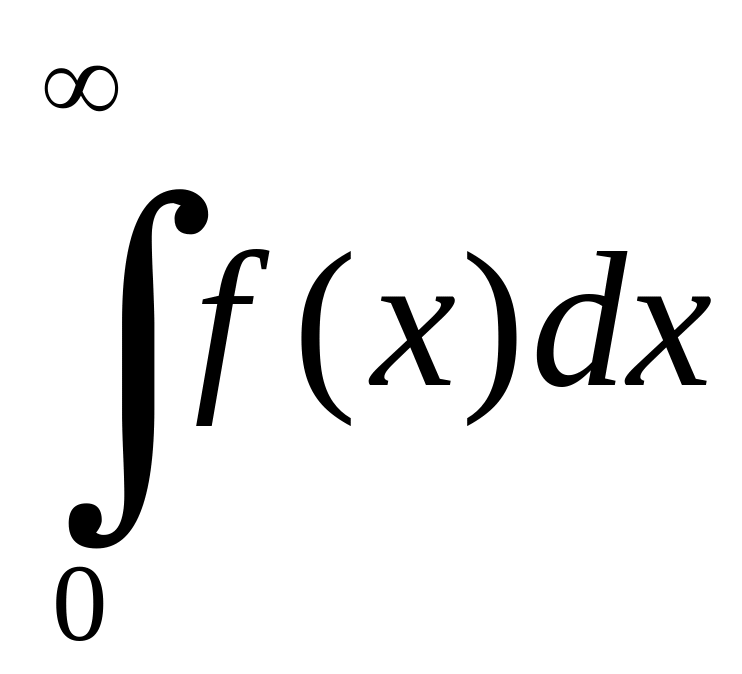, а тому ( парна) збігається і , причому

.

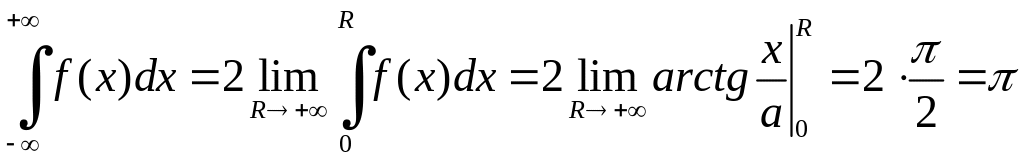Геометрично невласний збіжний інтеграл 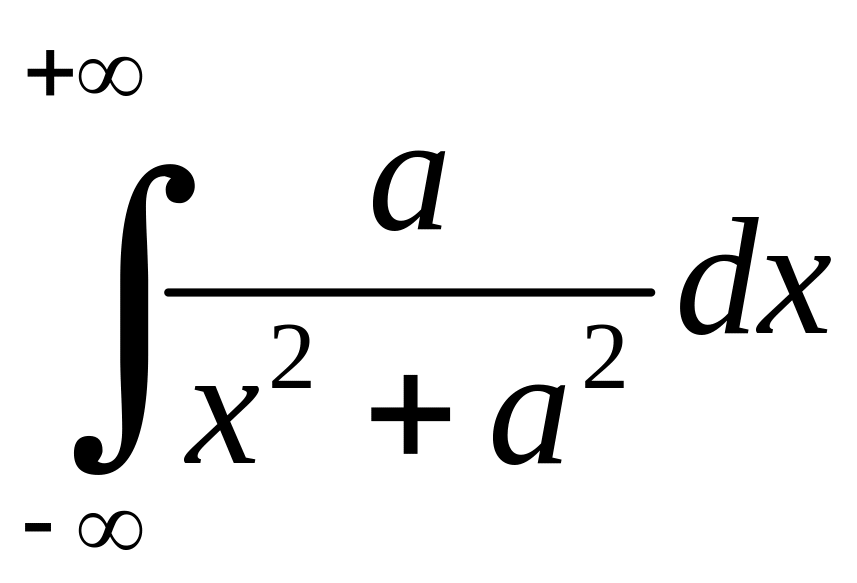виражає площу нескінченої криволінійної трапеції (рис. 3), яка дорівнює числу .

Приклад 6.4. В теорії ймовірностей важливу роль відіграють інтеграли

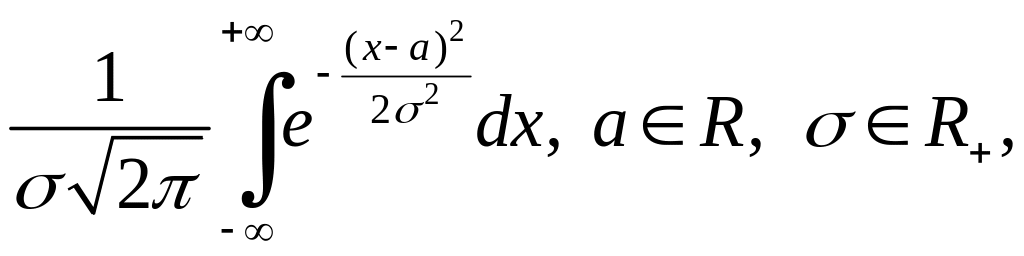
параметри.

Зрозуміло, що достатньо дослідити на збіжність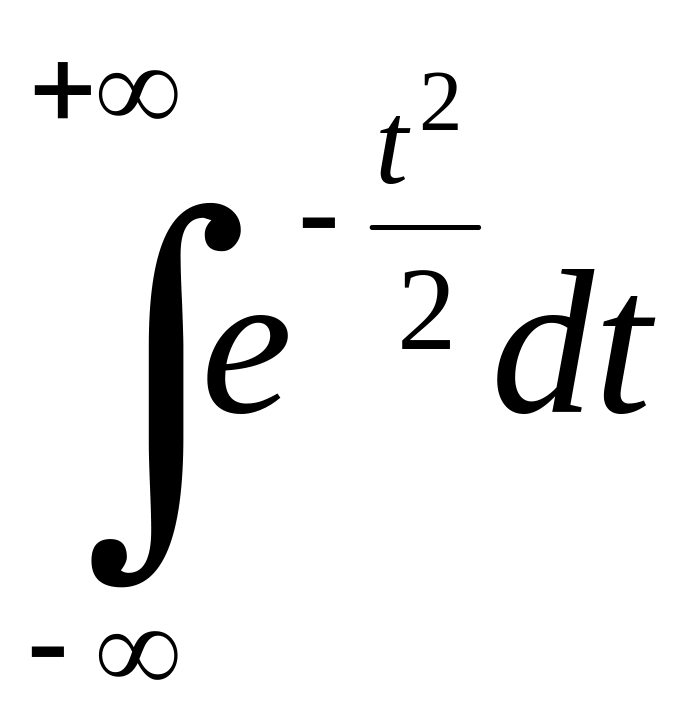 , оскільки заміна змінної зберігає властивість збігатись (чи розбігатись), а заміна приведе до інтеграла .

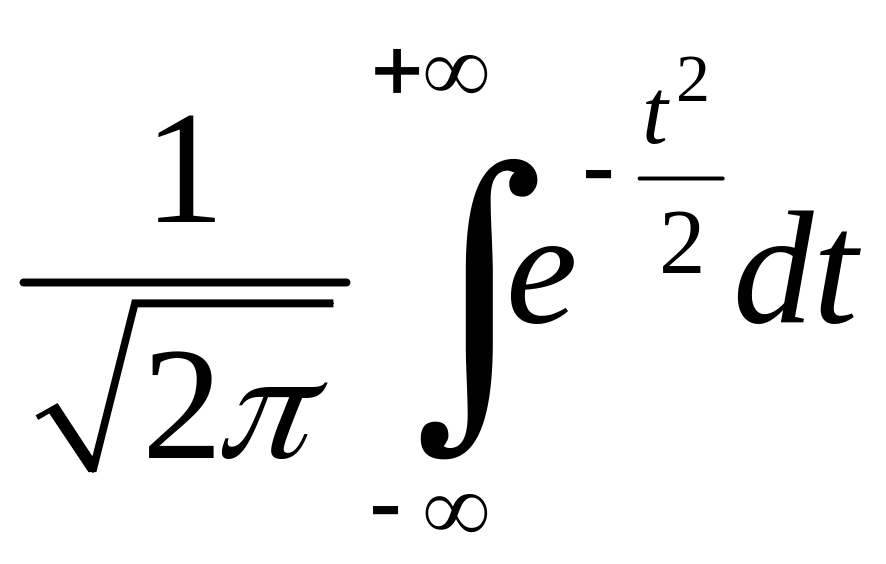Функція , парна, а тому достатньо дослідити на збіжність 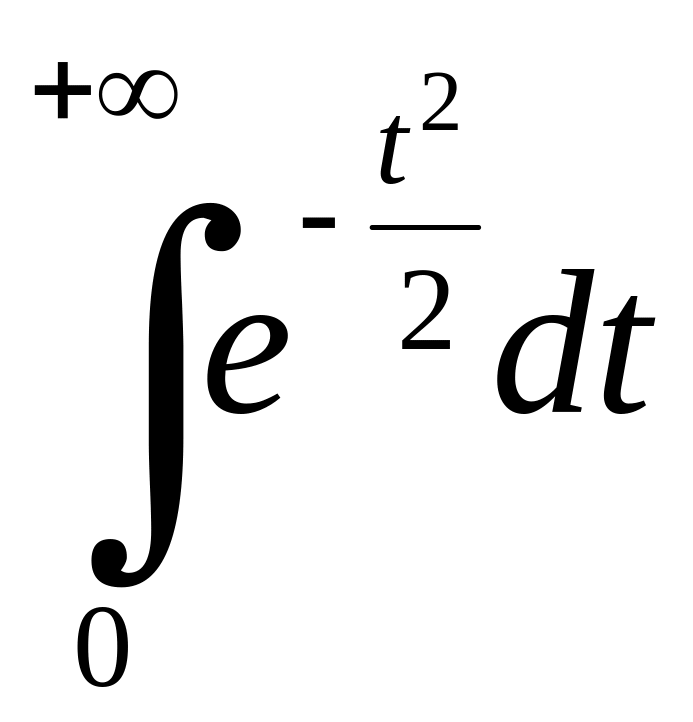. Коли зрозуміло, що , і

.

Отже, інтеграл

збігається при будь-яких і .

Інтеграл 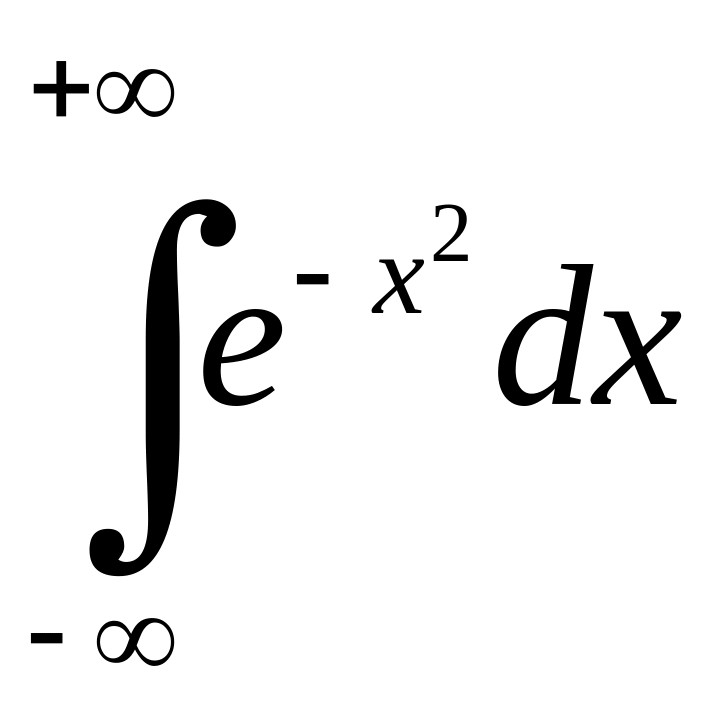називають інтегралом Ейлера-Пуассона.

Функцію

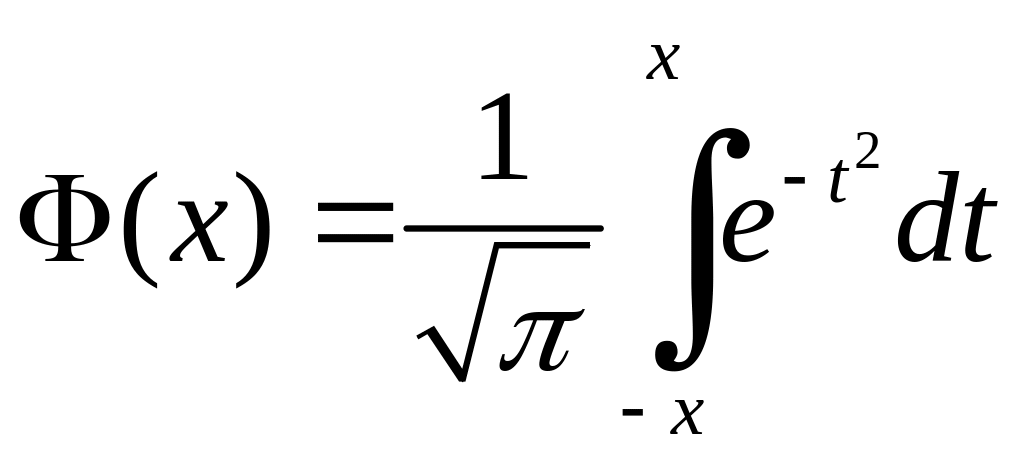
називають інтегралом імовірності похибок, її часто позначають символом (от англ. error - помилка). Ця функція непарна, нескінченне число раз диференційована на .

Приклад 6.5. У фізиці важливу роль відіграють інтеграли Френеля

.

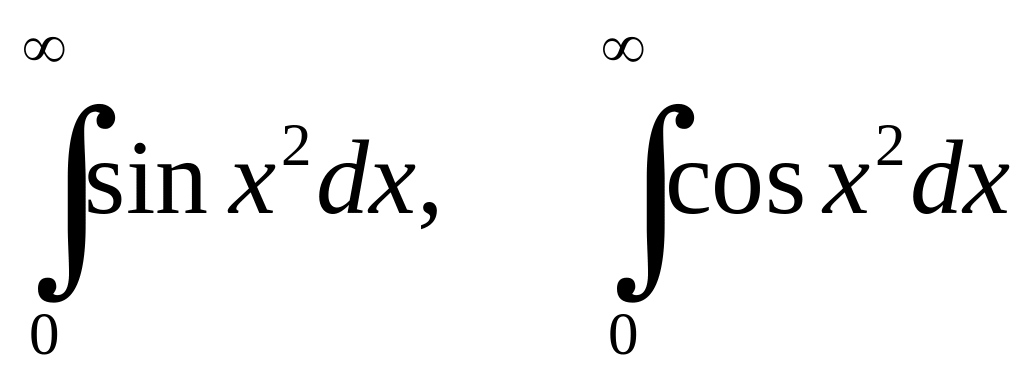Виконаємо заміну . Тоді, наприклад,

,

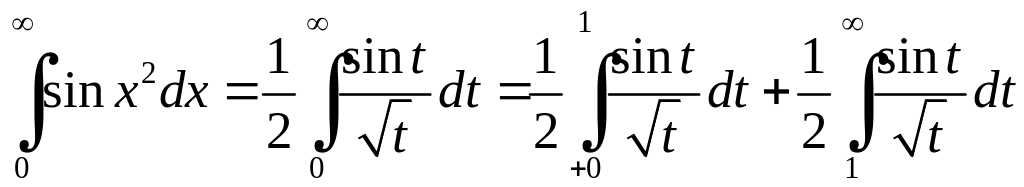де першій інтеграл справа – невласний інтеграл другого роду, а другий – першого роду. На функція додатна і , а тому 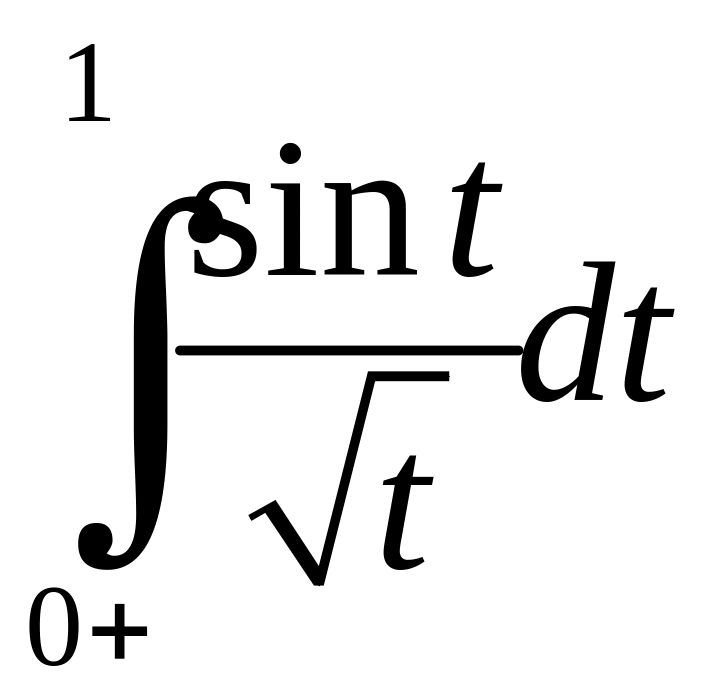існує. А 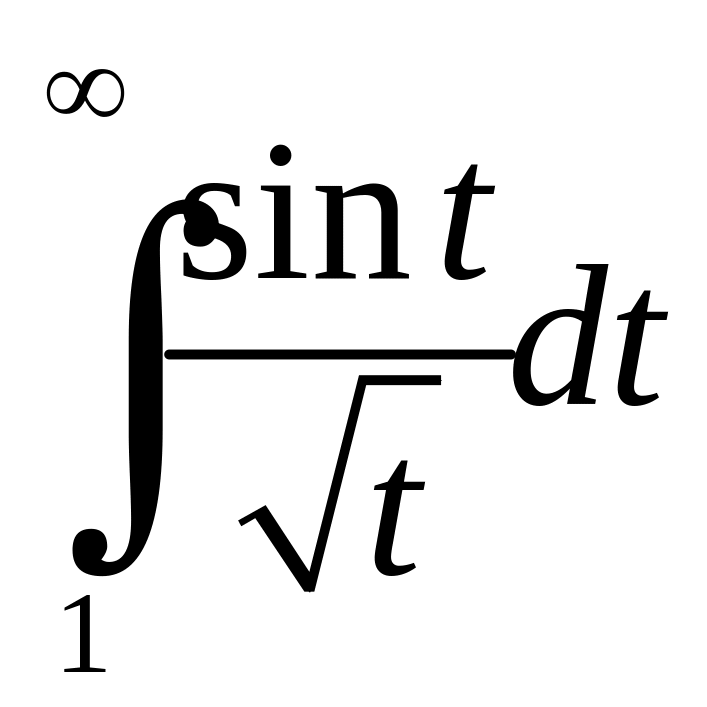збігається за умовою Діріхле, функція , а 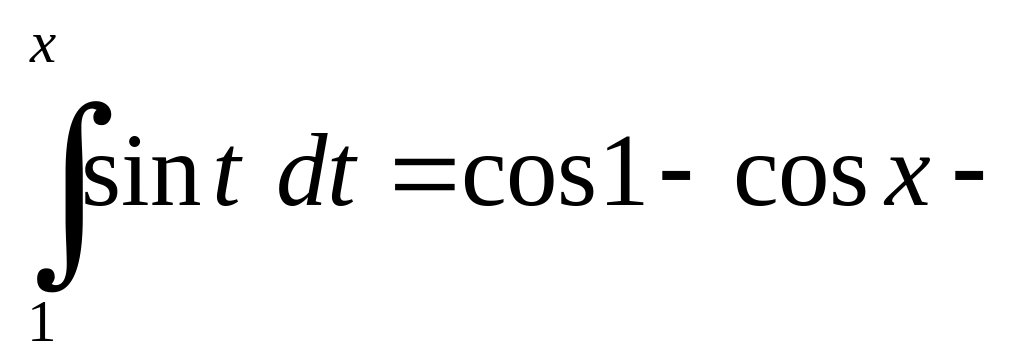обмежена функція числом 2 для будь-якого .

Відмітимо, що цей приклад цікавий тим, що 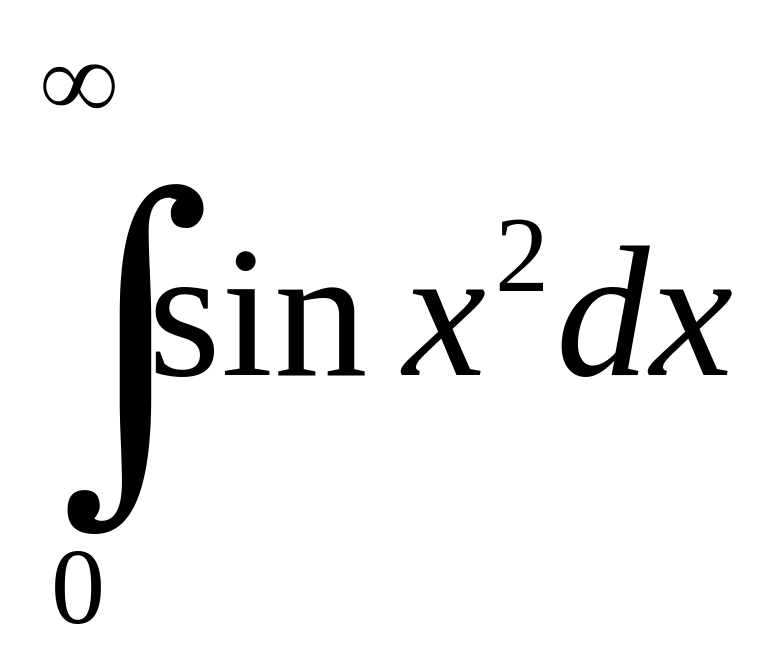збігається і при цьому , коли . Функція не має границі, коли .

Функція , - необмежена, коли , але

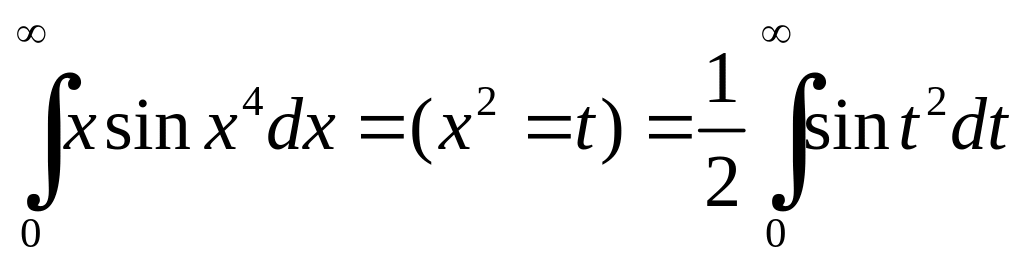
збігається. Приклад показує, що може бути збіжним і у випадку, коли необмежена при .

Приклад 6.6. Дослідити на збіжність

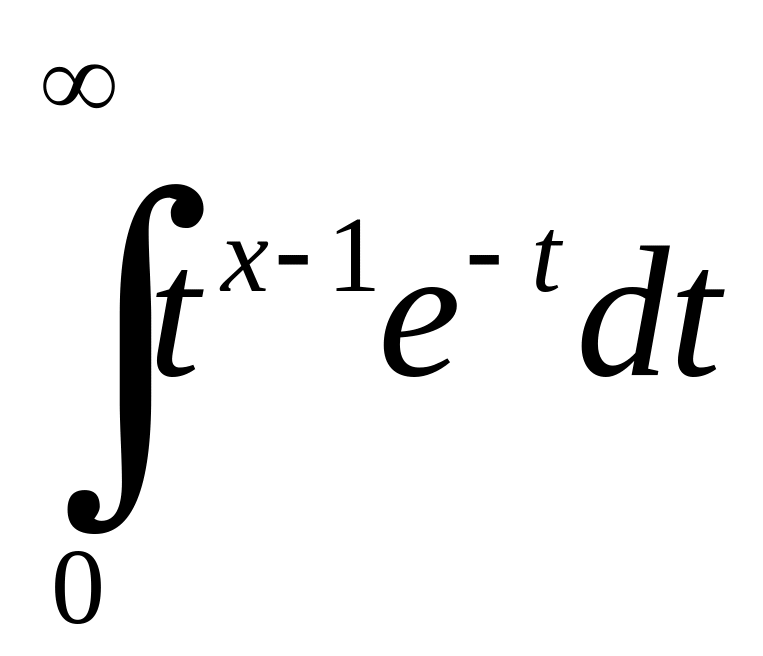, параметр.

Розв'язання. Запишемо інтеграл на проміжку як суму двох інтегралів

,

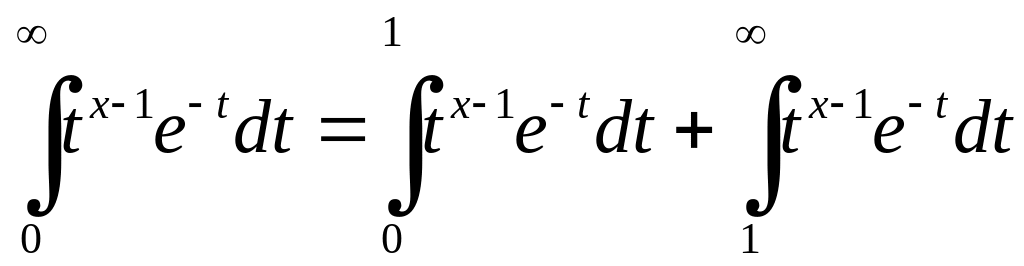перший є невласним інтегралом від необмеженої функції, коли , а другий – невласний інтеграл першого роду.

Оскільки функція невід’ємна на і , то можна взяти за мажоранту в першому випадку , а для 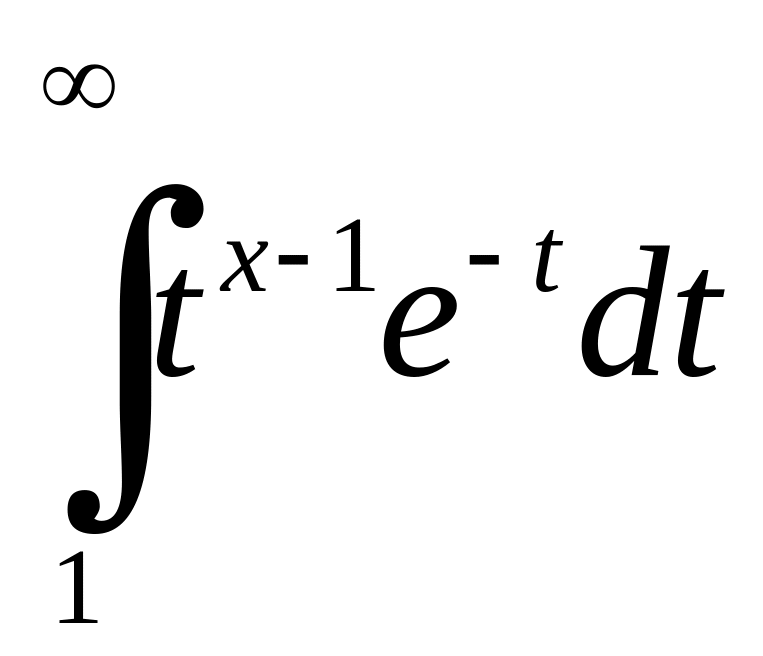візьмемо 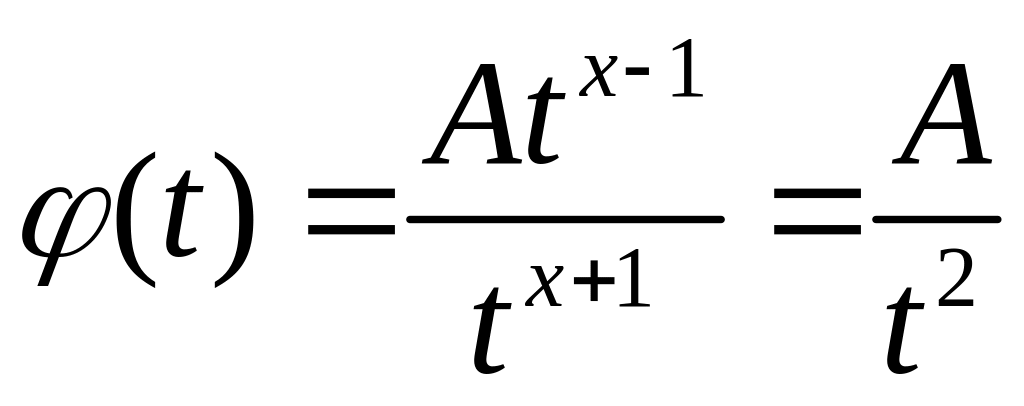, де . Оскільки 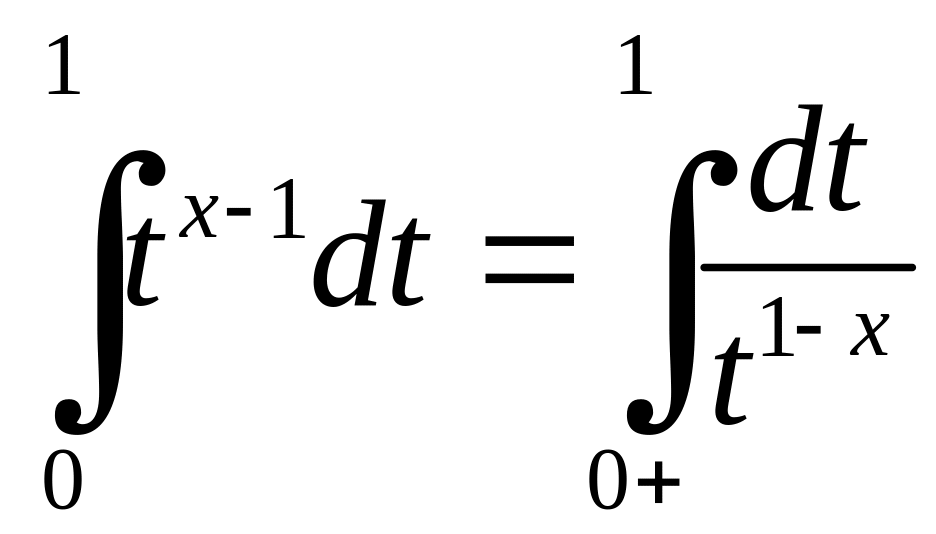і останній збігається, коли , або , то збігається, коли .

Означення. Гамма – функцією називається невласний інтеграл виду

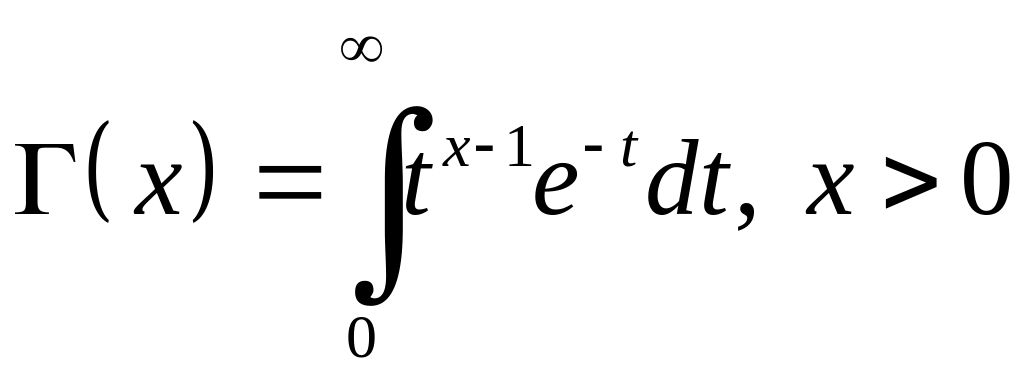
Функція після елементарних функцій є однією із самих важливих функцій в курсі аналізу і його застосувань. Вперше вона була розглянута Л.Ейлером в 1729 р., а тому інтеграл, який її визначає, називається ейлеровим інтегралом другого роду.

Серед властивостей цієї функції особливе місце займає формула приведення

,

яка переносить поняття факторіала на дробові і навіть комплексні значення аргументу. Основна властивість факторіала визначається формулою

.

Часто гамма – функцію називають факторіальною функцією.

В теорії гамма-функції доводиться формула доповнення:

звідки, як наслідок, одержимо, що

.

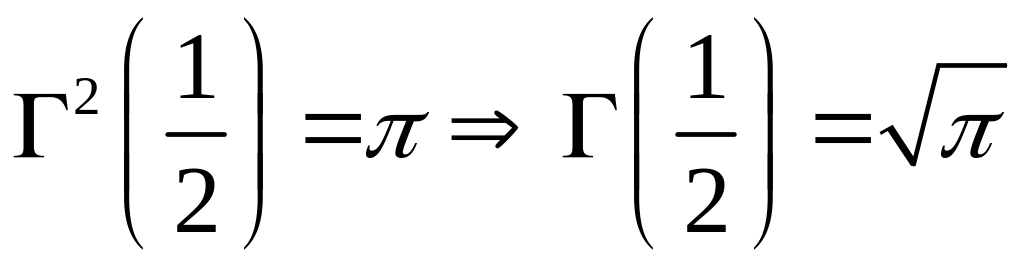Відмітимо, що

,

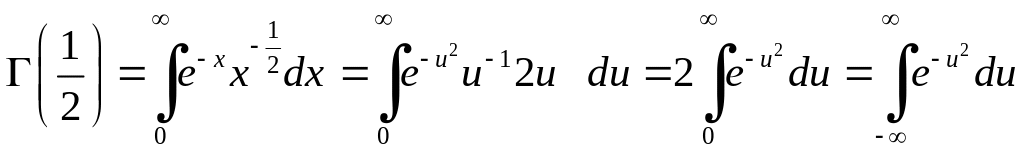одержали інтеграл Ейлера-Пуассона.

Із гамма-функцією тісно пов’язана бета-функція, яка визначається невласним інтегралом і який залежить від двох параметрів :

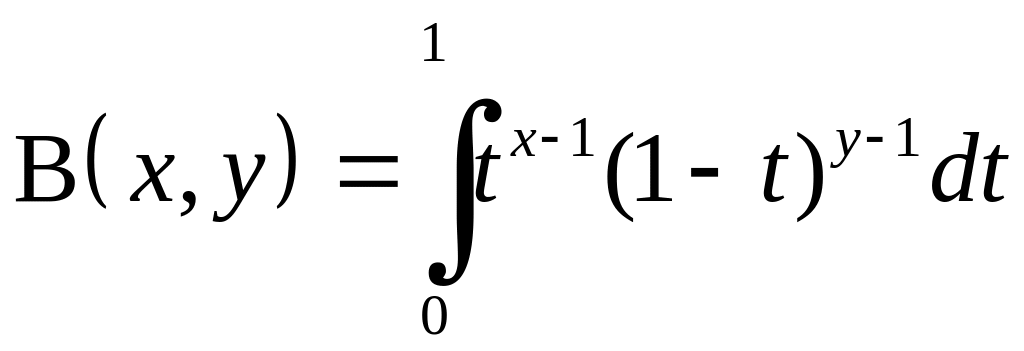
Інтеграл у правій частині називається ейлеровим інтегралом першого роду. Як буде показано пізніше

,

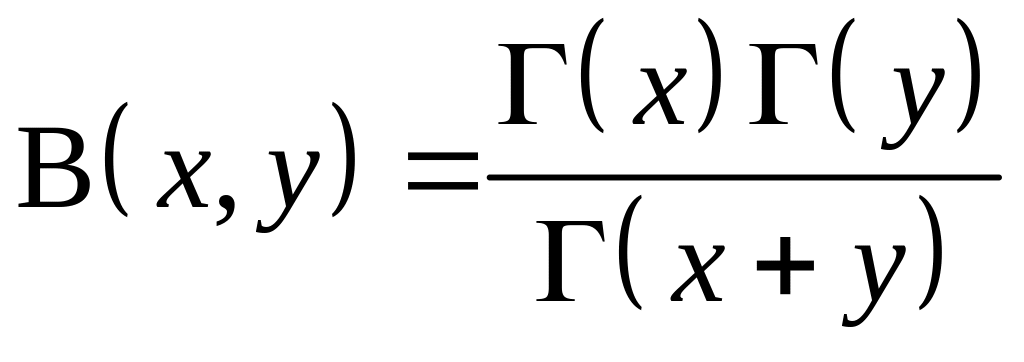а тому бета-функція визначена, коли .

І гамма-функція і бета-функція використовуються при обчисленні інтегралів. Так, наприклад,

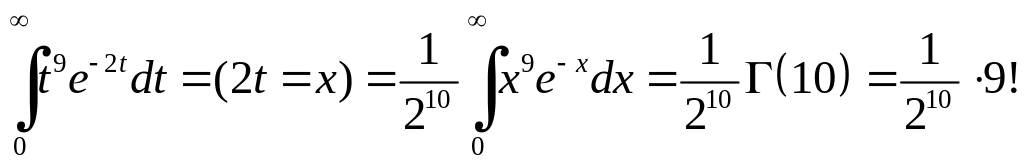
Приклад 6.7. Обчислити площу фігури, обмеженої кривою .

Розв'язання. Оскільки , то частини кривої лежать у першій та третій чвертях, симетрично відносно . Знайдемо площу фігури, використовуючи полярні координати:

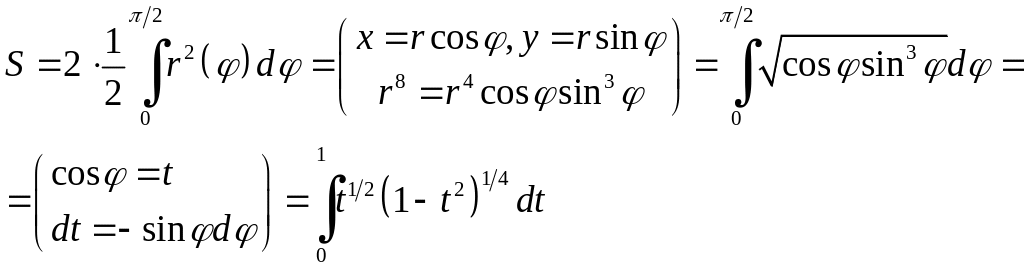
Заміна приведе до інтегралу, який визначає бета-функцію:

.

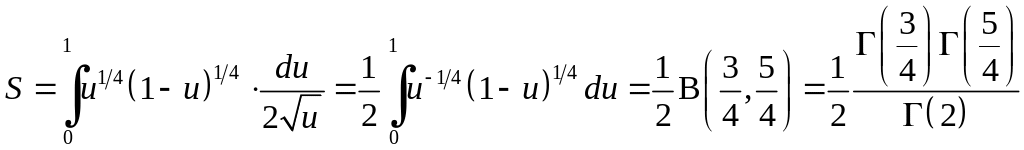За формулою (6.1) 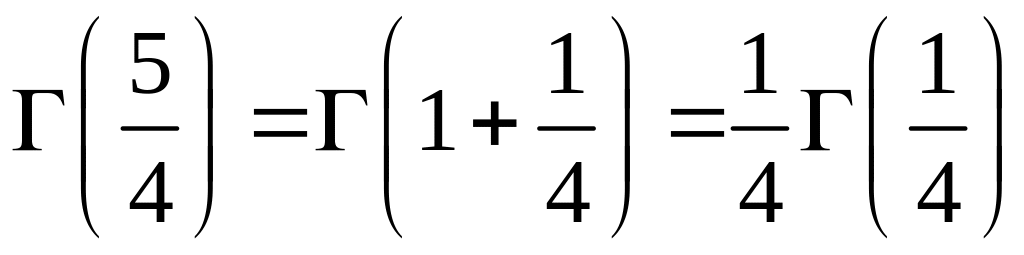, а за формулою (6.2):

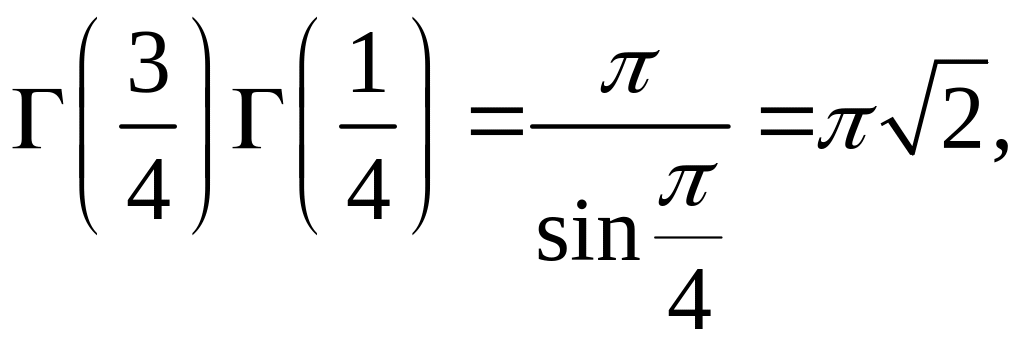
а тому ( )

.

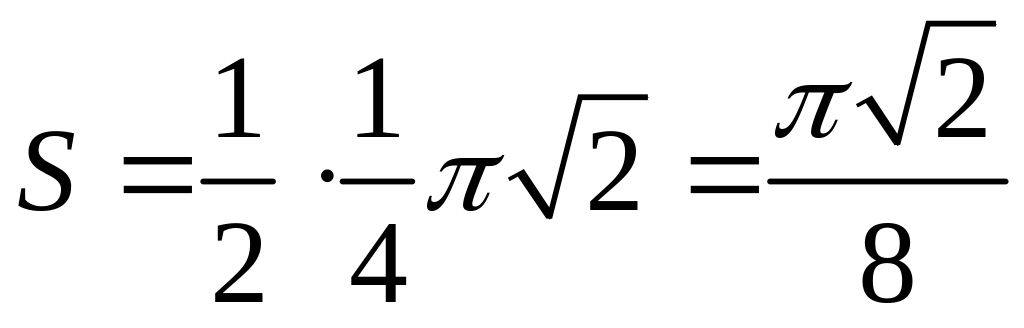У теорії ймовірностей гамма-функція визначає один із основних неперервних розподілів випадкової величини, що описує часи безвідмовної роботи багатьох приладів.

145