
- •Розділ IV. Невласні інтеграли
- •§ 1. Означення невласних інтегралів Рімана, приклади
- •§ 2. Абсолютна збіжність невласних інтегралів. Алгебраїчні властивості
- •§ 3. Заміна змінної в невласному інтегралі
- •§ 4. Інтегрування частинами в невласному інтегралі
- •§ 5. Достатні умови збіжності невласних інтегралів
- •§ 6. Головне значення (за Коші) розбіжних невласних інтегралів
- •Зрозуміло, що
§ 4. Інтегрування частинами в невласному інтегралі
Нехай
![]() дві функції, визначені і неперервні на
,
дві функції, визначені і неперервні на
,
![]() скінчене,
функції
скінчене,
функції
![]() також неперервні на
.
також неперервні на
.
Як
відомо, для будь-якого
![]() має місце формула інтегрування частинами
має місце формула інтегрування частинами
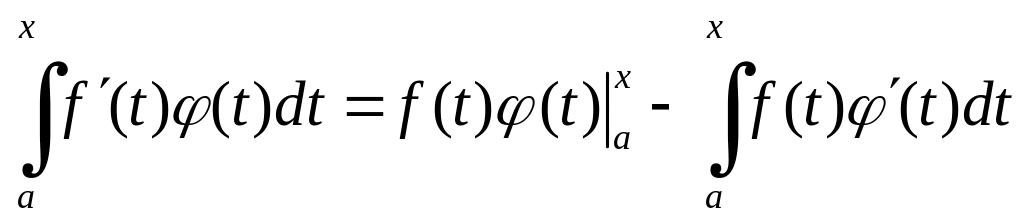 .
.
Якщо
два із цих трьох членів існують, коли
![]() прямує до
,
то третій член також має скінчену
границю. Зокрема, коли існують
прямує до
,
то третій член також має скінчену
границю. Зокрема, коли існують
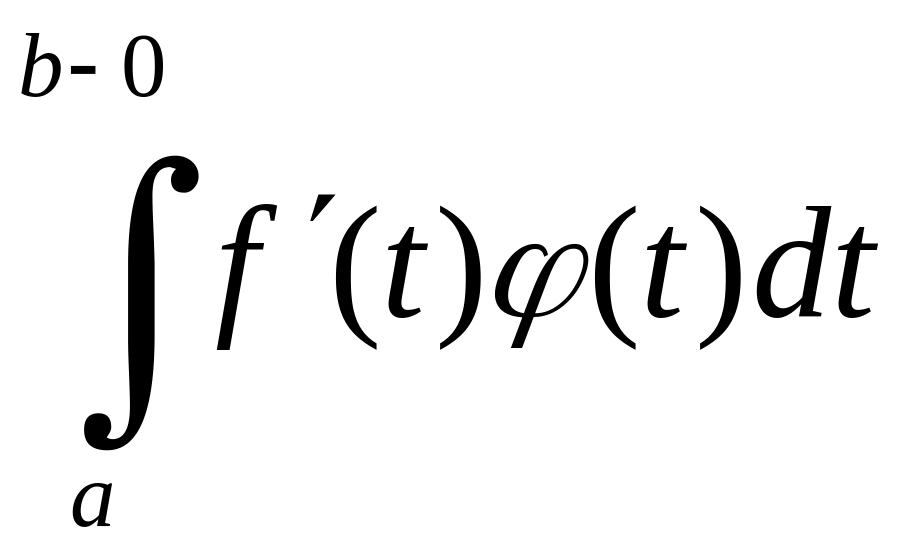 і
і
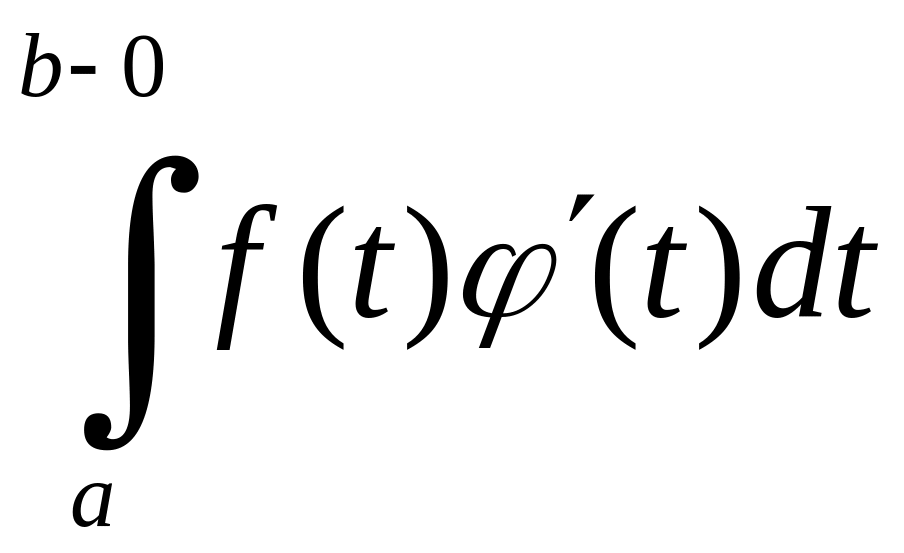 або існують
і
або існують
і
![]() ,
то
,
то
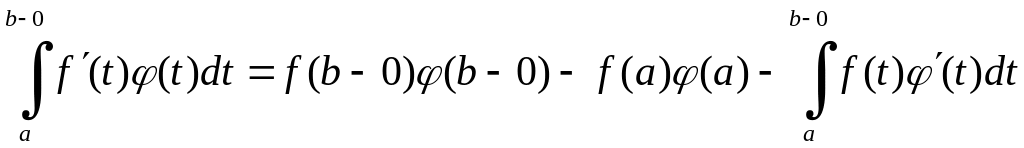 .
.
Таким чином, інтегрування частинами на некомпактному проміжку необхідно застосовувати обережно.
Приклад
4.1.
Розглянемо
функцію
![]() (називається „інтегральний синус”),
яка є первісною для функції
(називається „інтегральний синус”),
яка є первісною для функції
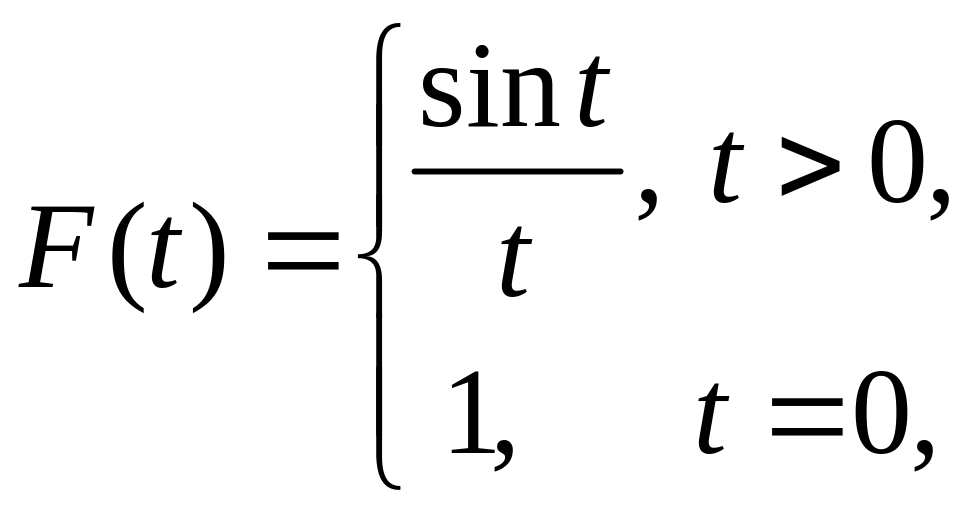
тобто
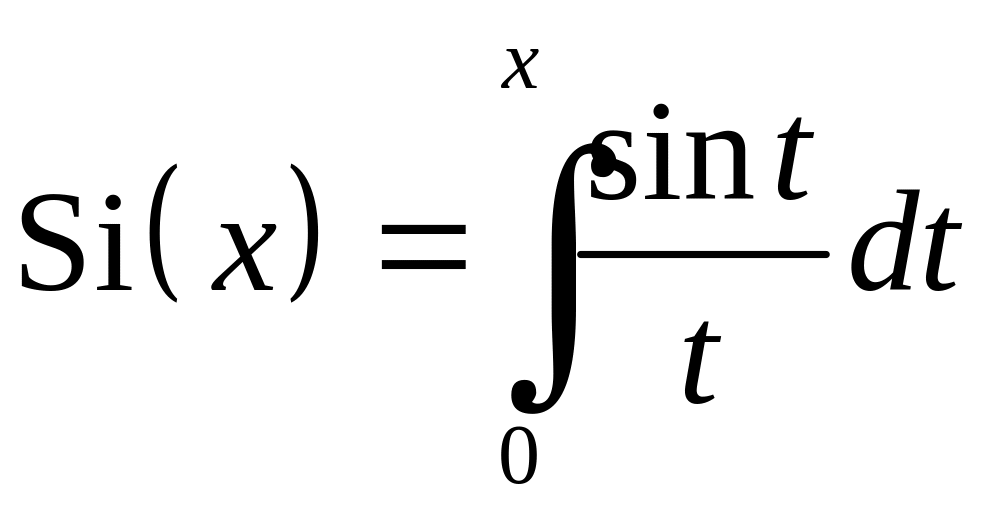 .
.
Покладемо
![]() ,
тоді
,
тоді
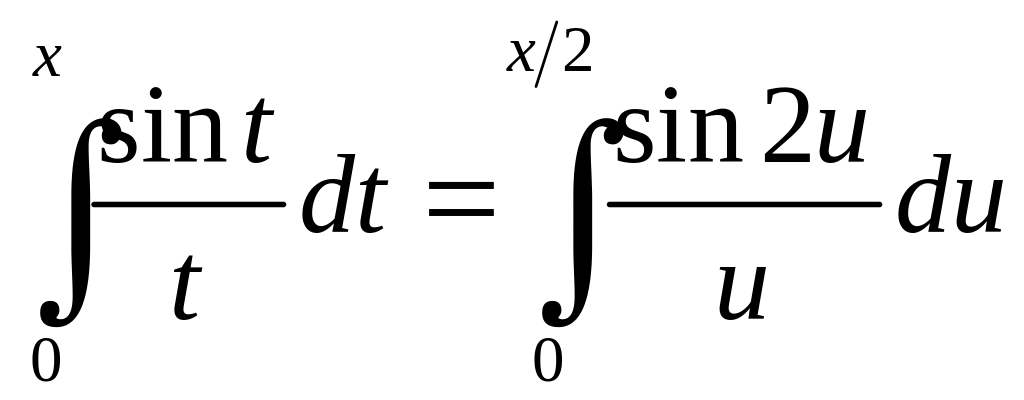 .
.
Але
![]() є похідна функції
є похідна функції
![]() .
.
Нехай
![]() ,
,
![]() .
Тоді
.
Тоді
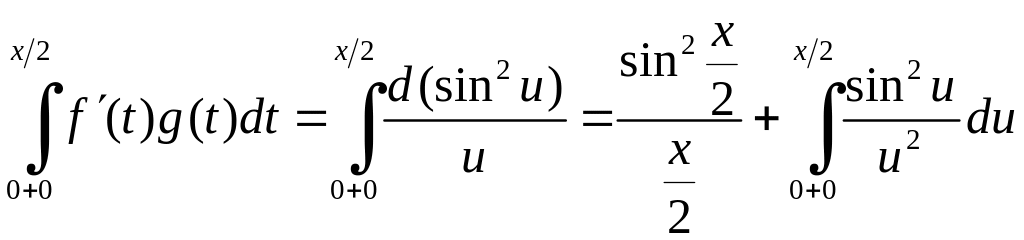 ,
,
оскільки
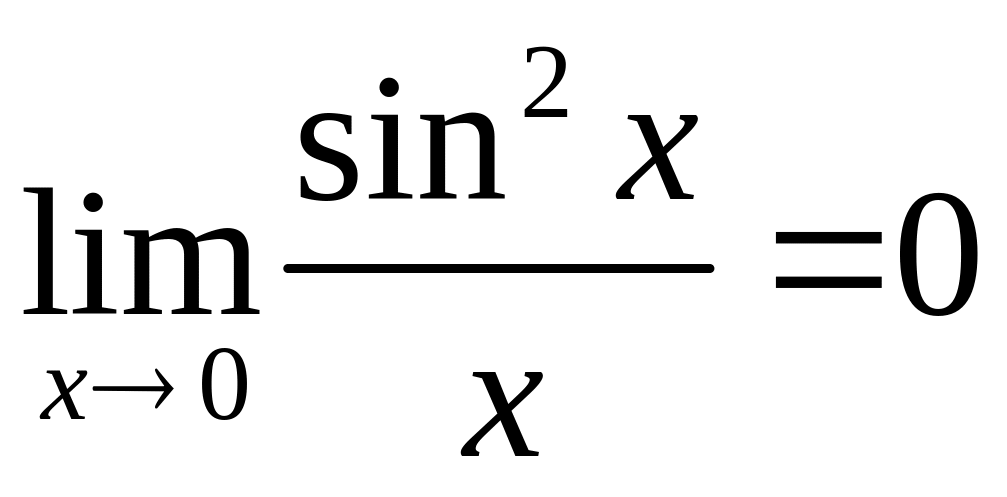 .
.
Нехай
тепер
![]() неперервна
на
неперервна
на
![]() функція, визначена як
функція, визначена як
![]() ,
,
 ,
,
![]() .
Маємо
.
Маємо
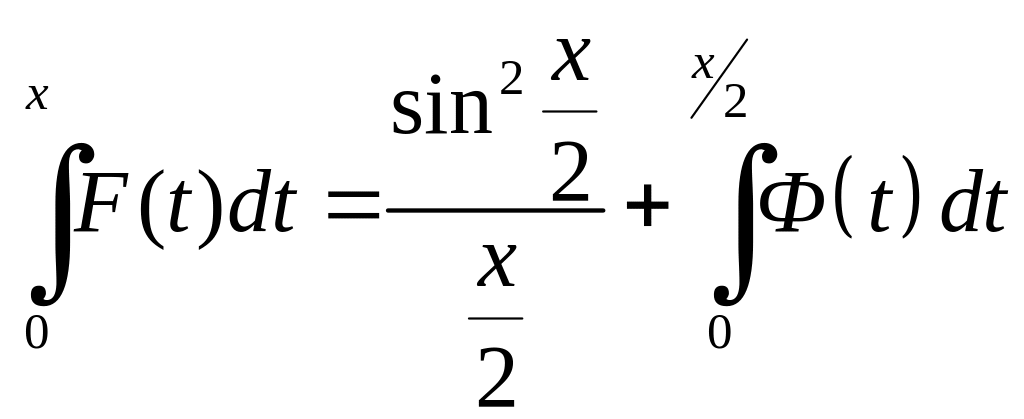 .
.
Зрозуміло,
що
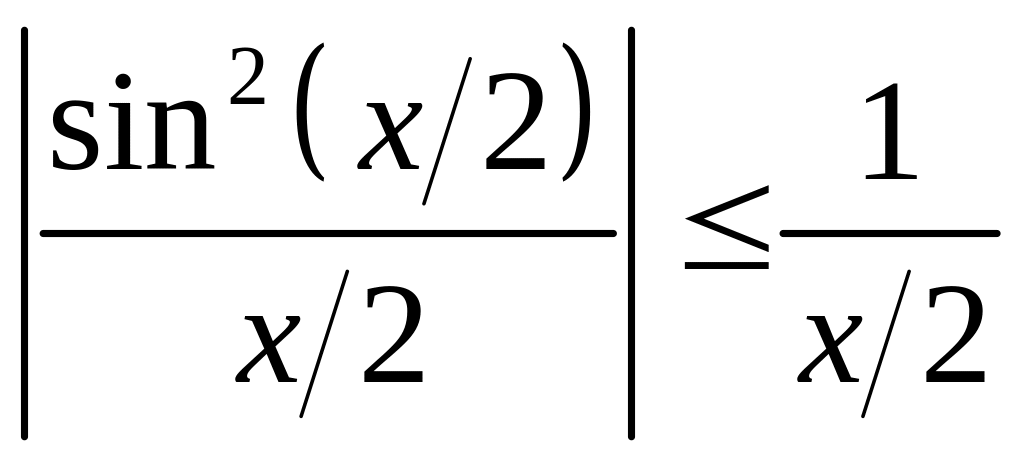 ,
,
а тому коли
прямує до нескінченості, то
,
,
а тому коли
прямує до нескінченості, то
 прямує до нуля. Тоді
прямує до нуля. Тоді
 . (4.1)
. (4.1)
Неважко
встановити збіжність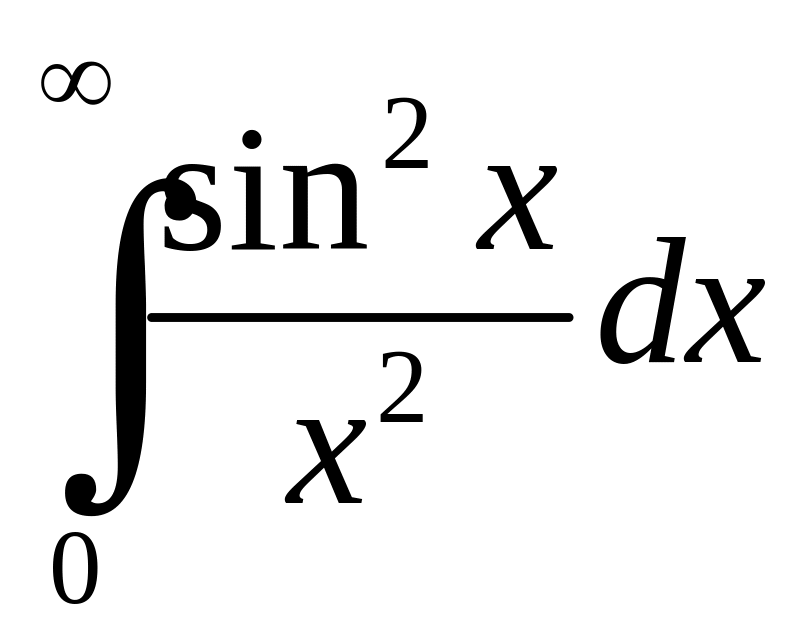 ,
оскільки
,
оскільки
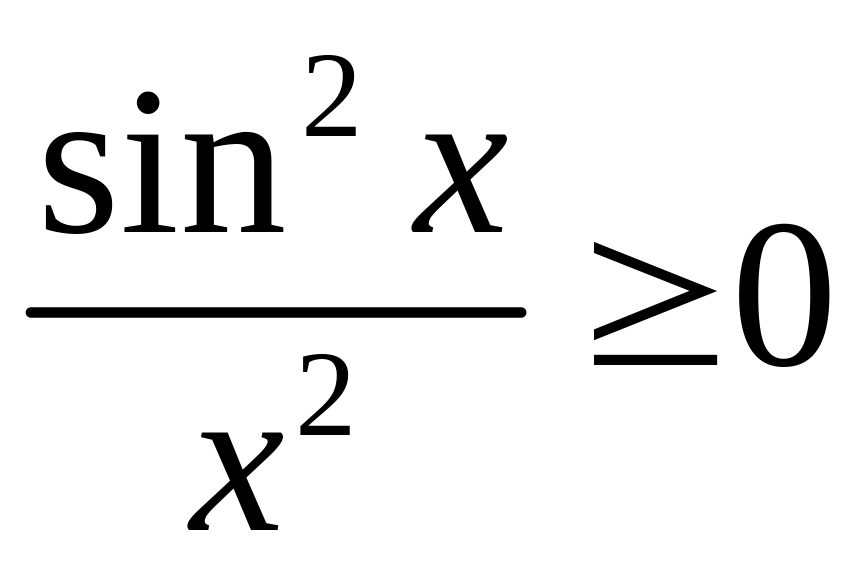 ,
:
,
:
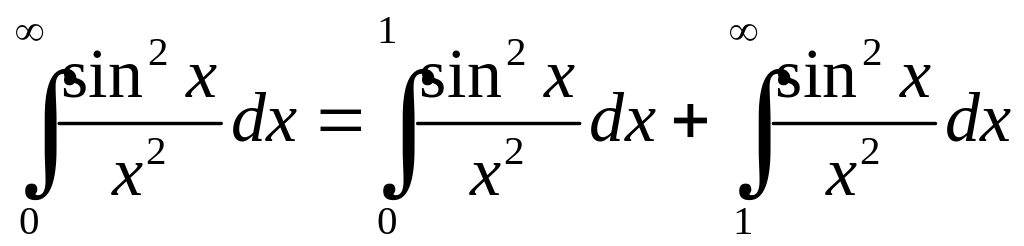
і на
будь-якому проміжку
,
![]()
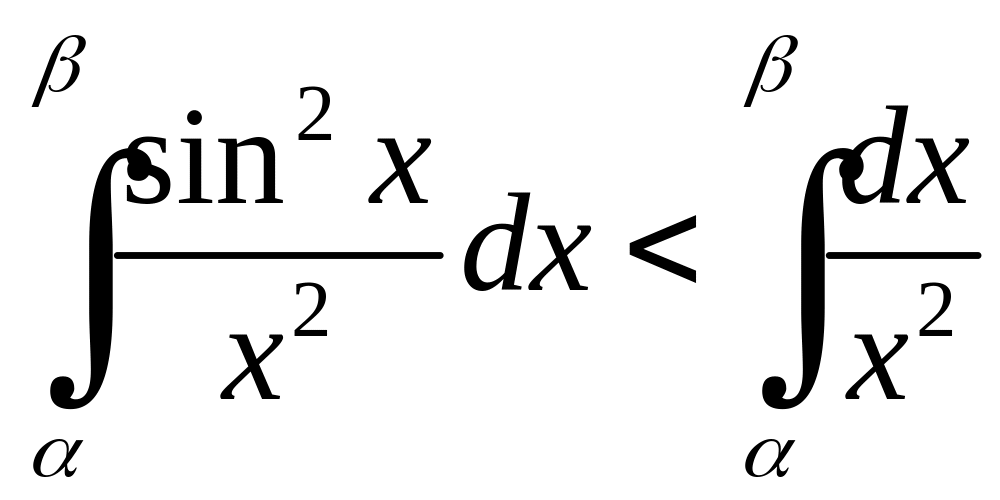 .
.
Як
відомо,
![]() збігається, а тому збігається (при тому
і абсолютно) і
.
збігається, а тому збігається (при тому
і абсолютно) і
.
Як буде
показано в теорії рядів
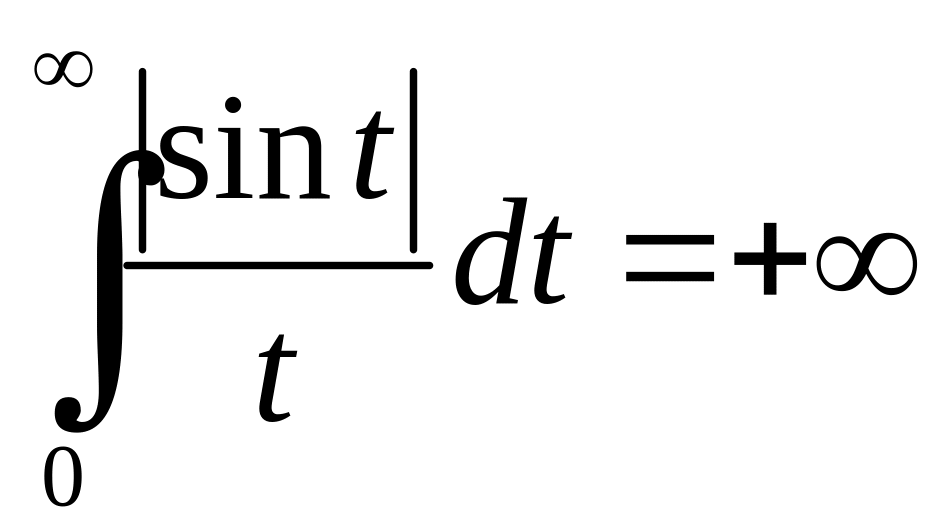 ,
отже, в цьому прикладі інтегрування
частинами переводить інтеграл, який
збігається абсолютно, у збіжний інтеграл,
але не абсолютно.
,
отже, в цьому прикладі інтегрування
частинами переводить інтеграл, який
збігається абсолютно, у збіжний інтеграл,
але не абсолютно.
§ 5. Достатні умови збіжності невласних інтегралів
Зупинимось
більш детально на умовах збіжності
невласних інтегралів на проміжку
![]() .
.
1.
Додатні функції.
Нехай
невід’ємна
функція на
,
неперервна на
![]() ,
,![]() .
.
Для
того, щоб існував
 необхідно і достатньо, щоб інтеграли
необхідно і достатньо, щоб інтеграли
 були обмежені зверху при будь-якому
були обмежені зверху при будь-якому
![]() .
.
Якщо
і
![]() дві
невід’ємні функції, визначені на
дві
невід’ємні функції, визначені на
![]() ,
неперервні на
,
,
неперервні на
,
![]() ,
і якщо
,
і якщо
![]() ,
то
,
то
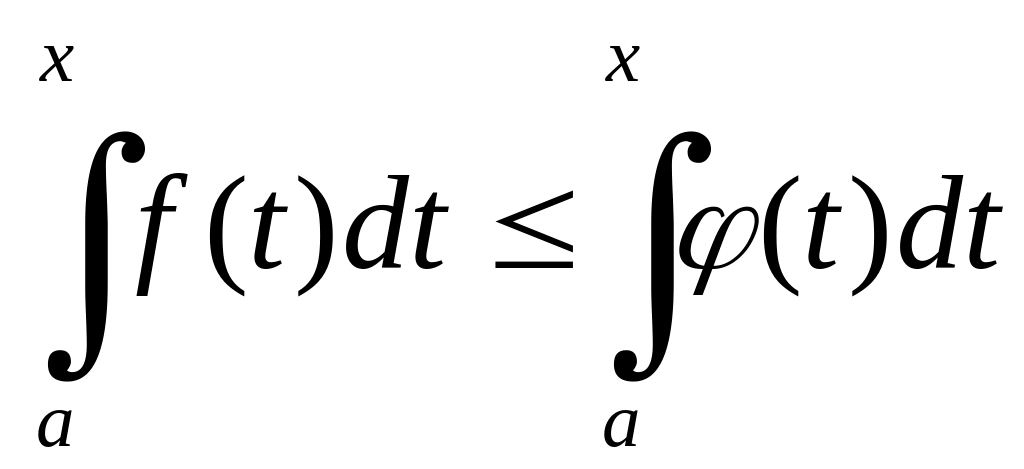 ,
,
і,
зрозуміло, що із збіжності
 слідує збіжність
;
якщо
буде розбіжним, то
також є розбіжним.
слідує збіжність
;
якщо
буде розбіжним, то
також є розбіжним.
Загальне
зауваження.
Нехай функція
![]() неперервна на будь-якому відрізку
неперервна на будь-якому відрізку
![]() .
Тоді, коли
достатньо велике, то
.
Тоді, коли
достатньо велике, то
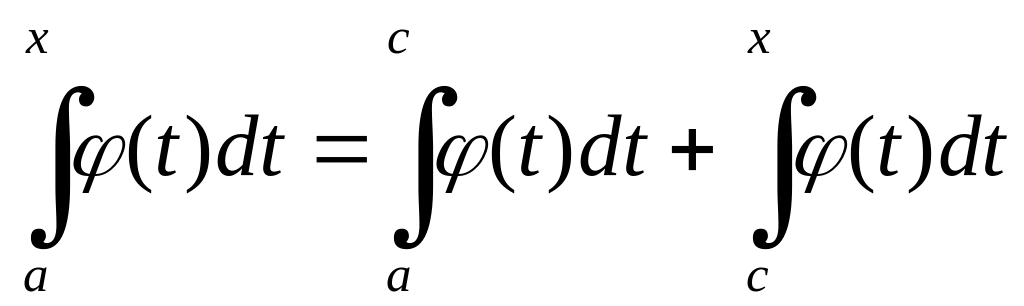
і,
зрозуміло, що для збіжності
 достатньо знати, чи збігається
достатньо знати, чи збігається
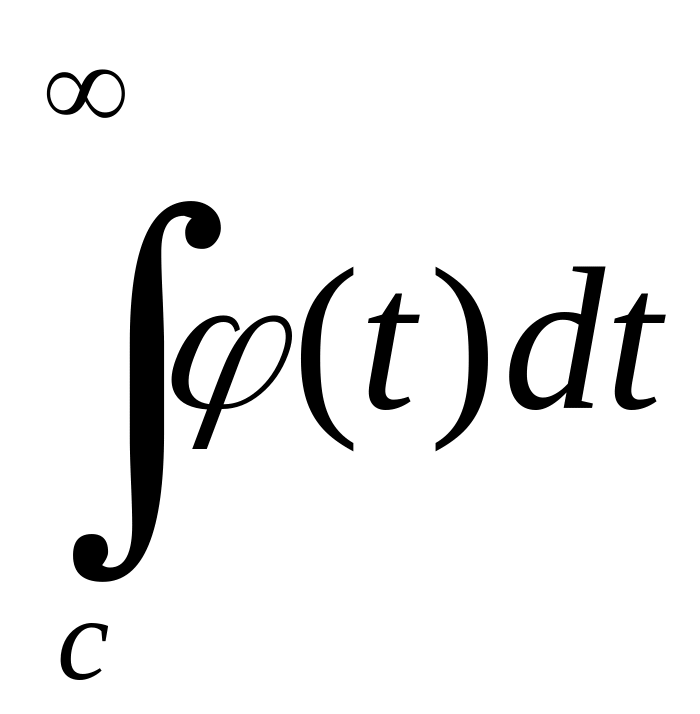 ,
,![]() .
Іншими словами, достатньо знати
поведінку
в околі
.
Іншими словами, достатньо знати
поведінку
в околі
![]() .
У деяких випадках асимптотичні розкладання
допоможуть оцінити цю поведінку.
Наприклад, для того, щоб збігався
достатньо, щоб при
.
У деяких випадках асимптотичні розкладання
допоможуть оцінити цю поведінку.
Наприклад, для того, щоб збігався
достатньо, щоб при
![]() функція
функція
![]() ,
де
,
де
![]() .
Тобто функції
.
Тобто функції
![]() ,
де
- параметр, можна вибрати за еталони
порівняння.
,
де
- параметр, можна вибрати за еталони
порівняння.
2.
Абсолютна і умовна збіжність. Нехай
інтегруєма,
наприклад, неперервна функція на відрізку
![]() при будь-якому
при будь-якому
![]() ,
а
- невід’ємна інтегруєма функція на тому
ж проміжку
така, що існує
,
і знайдеться таке число
,
а
- невід’ємна інтегруєма функція на тому
ж проміжку
така, що існує
,
і знайдеться таке число
![]() ,
що для
,
що для
![]() виконується нерівність
виконується нерівність
![]() .
Тоді
.
Тоді
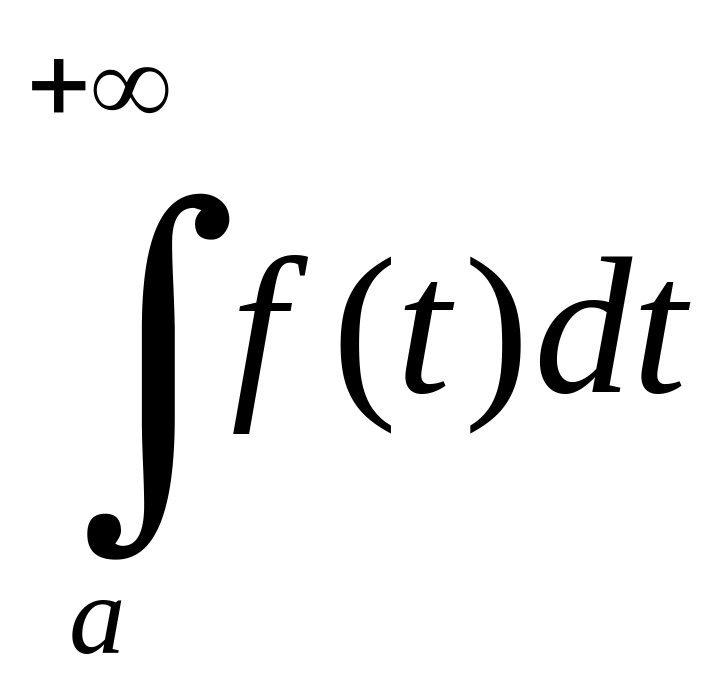 буде абсолютно збіжним.
буде абсолютно збіжним.
Приклад
5.1.
Нехай
![]() ,
,
![]() і
і
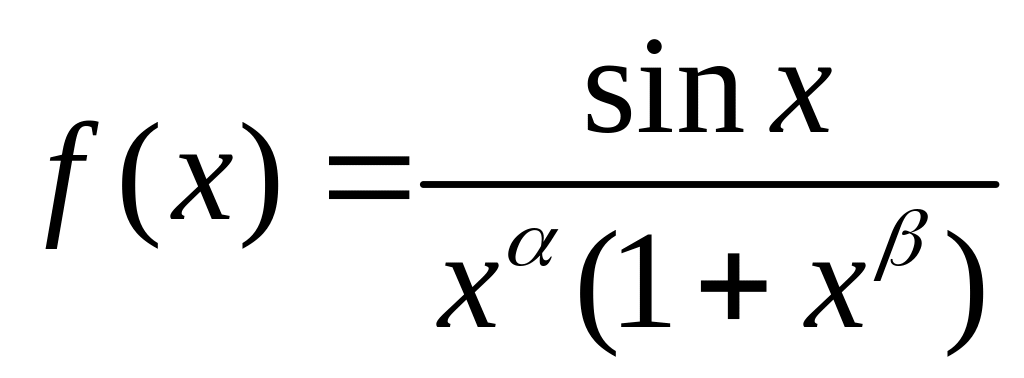 .
Тоді для достатньо великих
маємо
.
Тоді для достатньо великих
маємо
 .
.
Якщо
![]() ,
то
абсолютно збігається.
,
то
абсолютно збігається.
Основою
доведення збіжності (неабсолютної)
невласного інтеграла являється критерій
Коші: для того, щоб існував
необхідно і достатньо, щоб
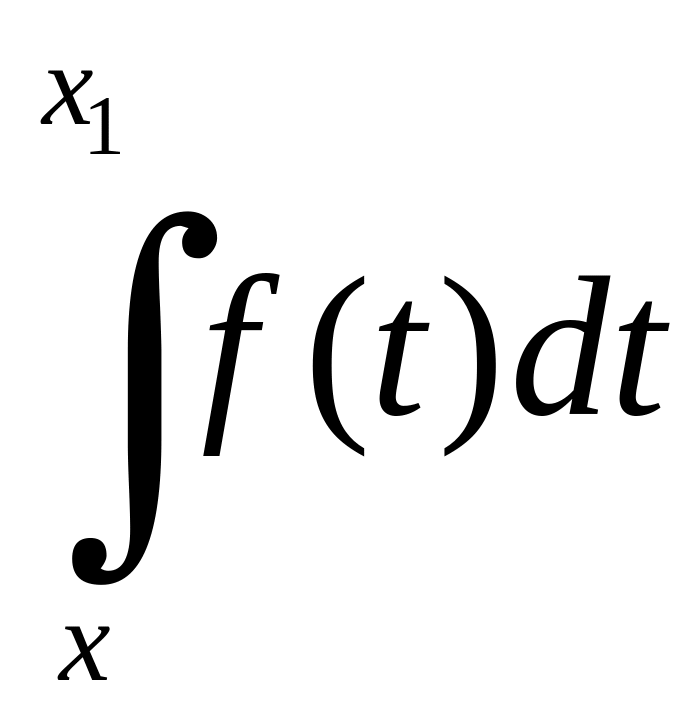 прямував до нуля, коли
і
прямував до нуля, коли
і
![]() прямують незалежно до
.
прямують незалежно до
.
Зрозуміло, що перевірка на збіжність за допомогою цього критерію не зовсім проста (точніше, далеко не проста).
Розглянемо
окремо випадок, коли
та
неперервні при![]() ,
а
,
а
![]() і
їх первісні. Тоді для будь-яких
і
їх первісні. Тоді для будь-яких
![]()
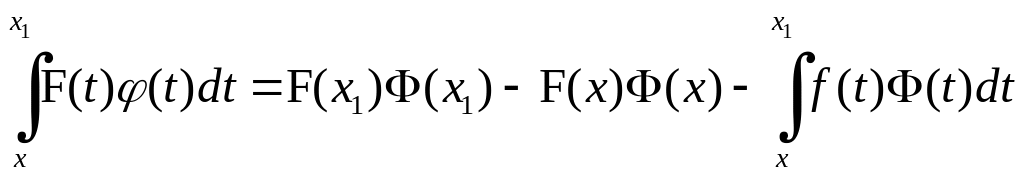 ,
,
звідки
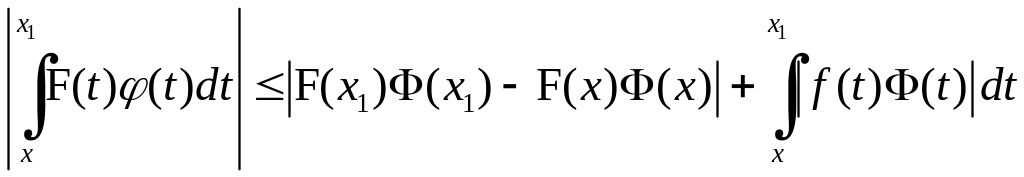 .
.
Припустимо,
що
![]() обмежена на
тобто
обмежена на
тобто
![]() ,
,
![]() і
абсолютно збігається.
і
абсолютно збігається.
Тоді
![]() і
і
![]() прямують до нуля, коли
прямують до нуля, коли
![]() і
і
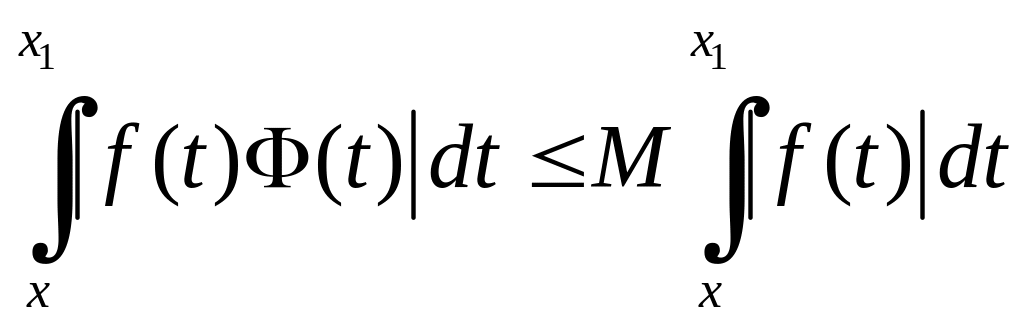 .
.
Тим
самим доведено, що
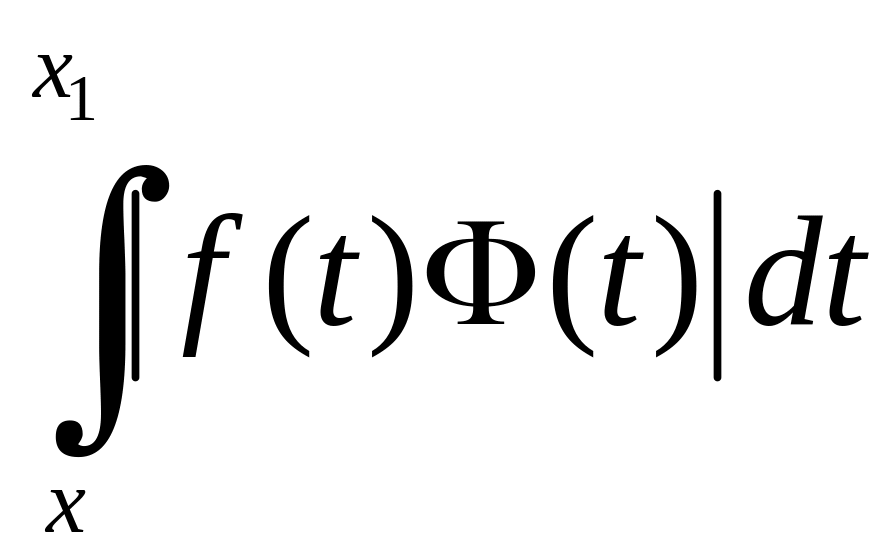 прямує до нуля, а тим більш і
прямує до нуля, а тим більш і
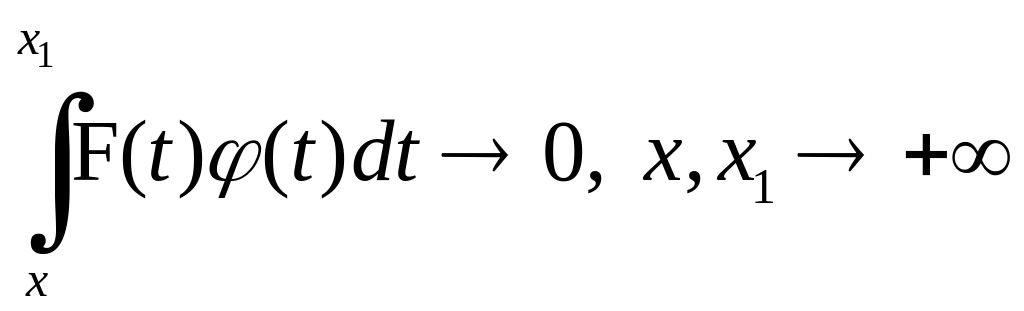 .
.
Приклад
5.2.
Нехай![]() ,
.
Якщо
,
то, оскільки
,
.
Якщо
,
то, оскільки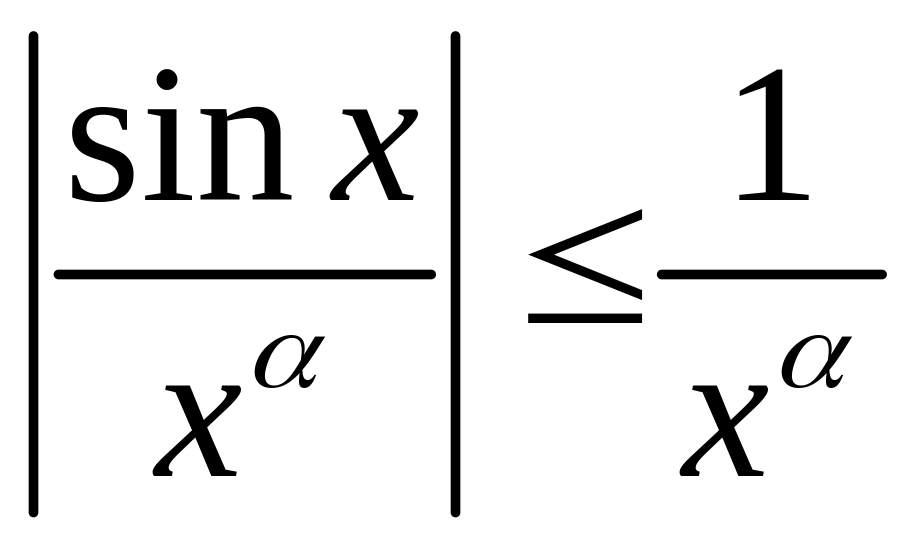 ,
то
,
то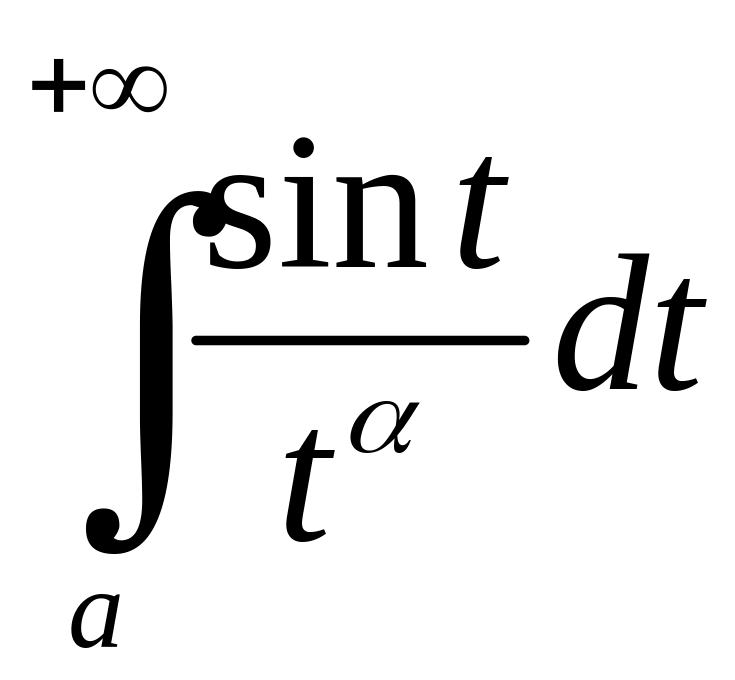 ,
абсолютно збігається.
,
абсолютно збігається.
Якщо
![]() ,
то покладемо
,
то покладемо
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Оскільки
,
то
.
Оскільки
,
то
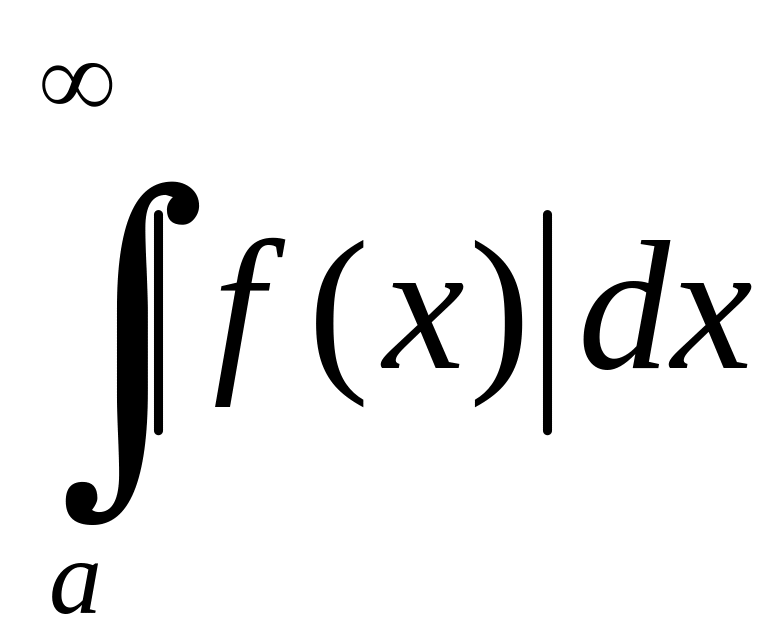 збігається,
,
збігається,
,
![]() і
і
 збігається, коли
.
Зрозуміло, що буде збіжним і
збігається, коли
.
Зрозуміло, що буде збіжним і
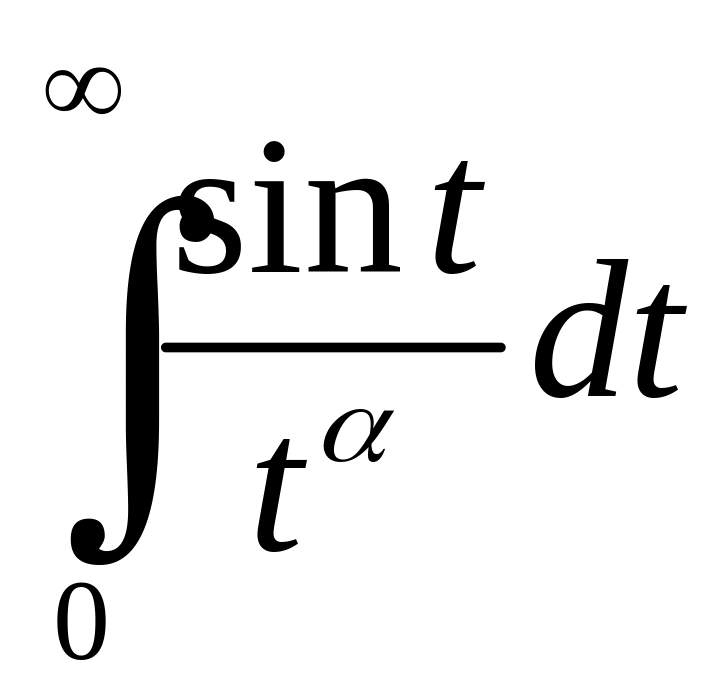 ,
.
,
.
Таким чином, якщо підсумувати все вищесказане, то:
1) якщо
і
невід’ємні функції, визначені на
і інтегруємі на будь-якому відрізку
![]() ,
причому
,
причому
![]() (
(![]() називають мажорантою для
,
а
називають мажорантою для
,
а
![]() мінорантою
для
),
то із збіжності
слідує збіжність і
,
а із розбіжності
слідує розбіжність
мінорантою
для
),
то із збіжності
слідує збіжність і
,
а із розбіжності
слідує розбіжність
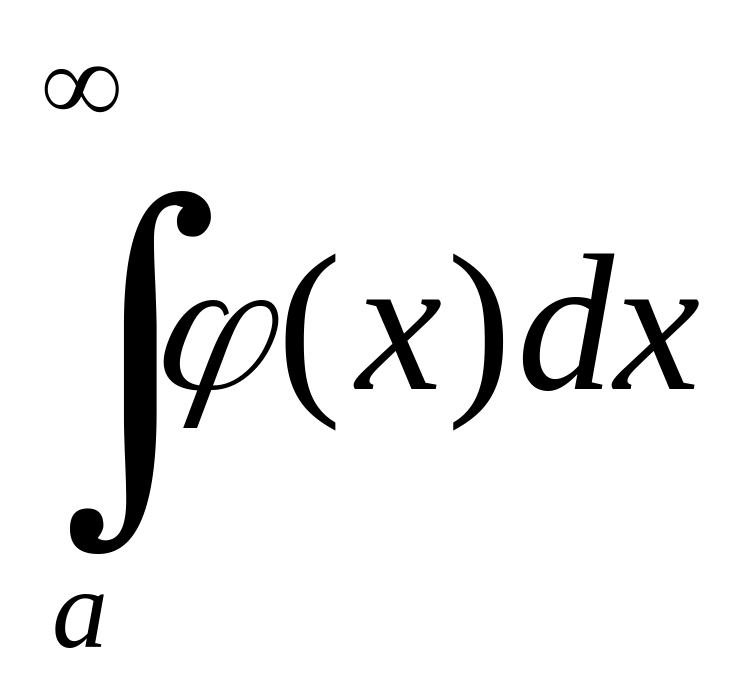 .
Коротко кажучи: “якщо збігається
мажоранта, то збігається і міноранта.
А якщо розбігається міноранта, то
розбігається і мажоранта ”;
.
Коротко кажучи: “якщо збігається
мажоранта, то збігається і міноранта.
А якщо розбігається міноранта, то
розбігається і мажоранта ”;
2) нехай
інтегруєма
функція на
![]() ,
де
,
де
![]() будь-яке
число із
,
і
нескінченно
мала при
будь-яке
число із
,
і
нескінченно
мала при
![]() ,
того же порядку, що функція
,
.
Тоді
збігається, коли
,
і розбігається, коли
,
того же порядку, що функція
,
.
Тоді
збігається, коли
,
і розбігається, коли
![]() ;
;
3) нехай
інтегруєма
функція на будь-якому
![]() і має при
і має при
![]() той же порядок росту, що і функція
той же порядок росту, що і функція
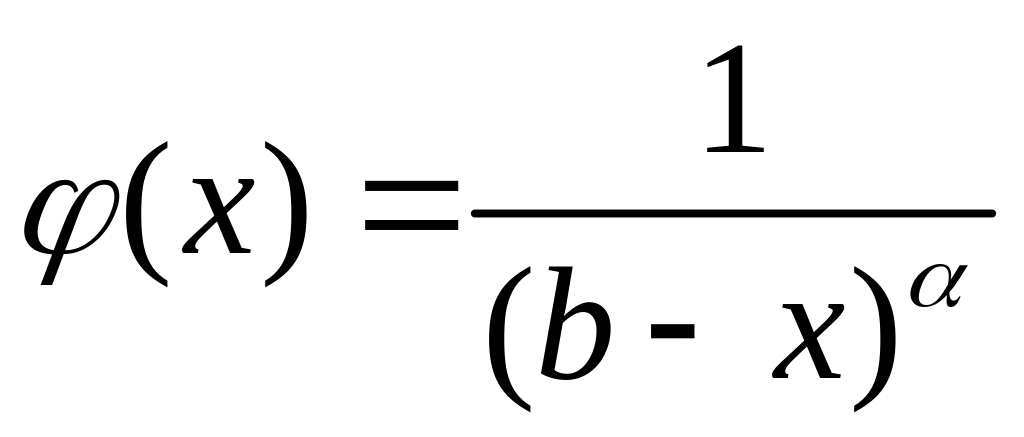 ,
.
,
.
Тоді
збігається, коли
![]() ,
і розбігається, коли
,
і розбігається, коли
![]() ;
;
4) теорема
(умова Абеля).
Нехай функції
і
визначені на
,
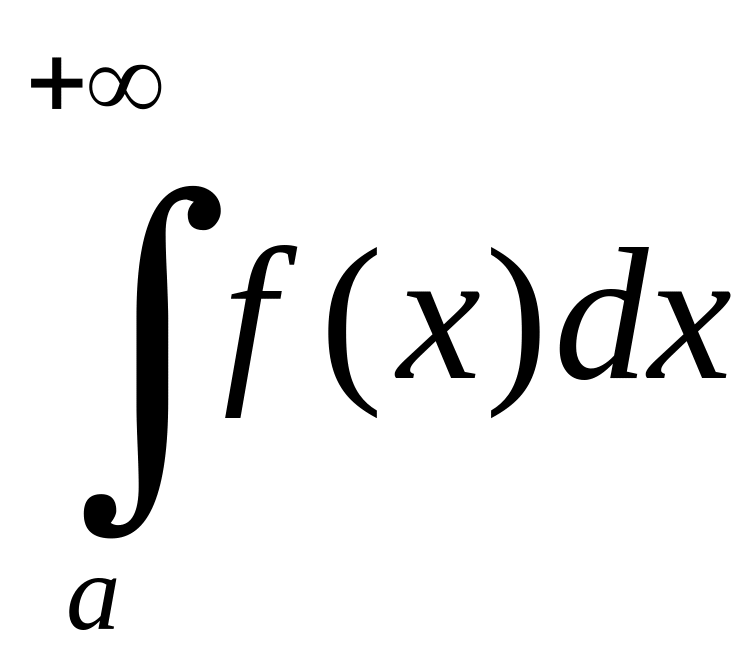 збігається, а функція
монотонна
і обмежена. Тоді інтеграл
збігається, а функція
монотонна
і обмежена. Тоді інтеграл
 збігається.
збігається.
5) теорема
(умова Діріхле).
Нехай
і
визначені на
,
функція
має обмежену первісну
,
,
а функція
монотонно прямує до нуля, коли
.
Тоді інтеграл
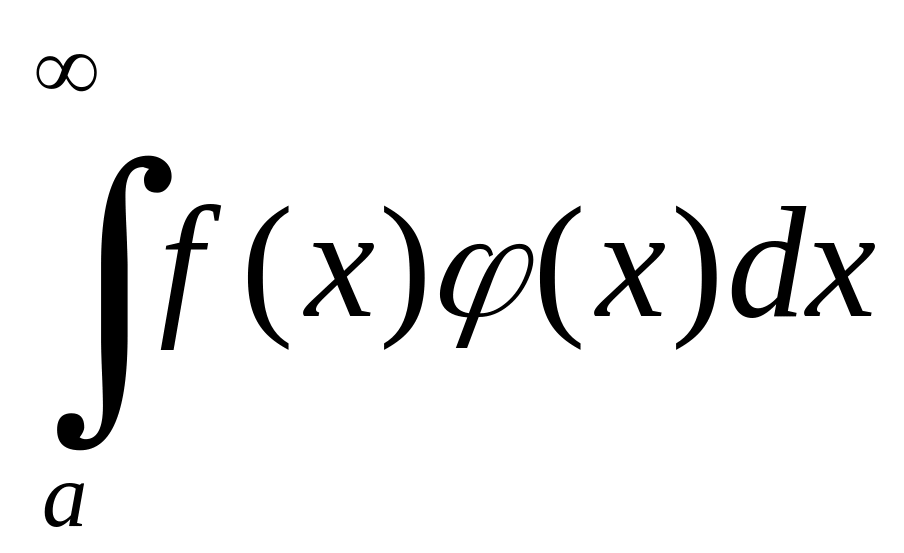 збігається.
збігається.
