3 Шаг: Запишем систему уравнений:

Простейшие преобразования (решать надо начинать с третьего уравнения, затем второе и последним первое уравнение системы) привели к ответам: х=1, y=2, z=3. Решение системы уравнений методом Гаусса используют чаще, чем другие способы, поэтому важно разбираться в данном алгоритме

Постараюсь метод Крамера объяснить подробно, по минимуму говоря математическим языком, использование формулы Крамера при решении систем уравнений.

Запись формулы Крамера запоминается легко, наверное потому, что запоминать вроде и нечего:

Итак, формулы позволяют рассчитать те переменные, которые Вам требуется найти в системе уравнений. В каждой системе может быть разное количество переменных, начиная с двух. Я написала всего три формулы, соответственно для трех неизвестных х, y и z.

Почему именно для трех? Наверное потому, что чаще всего предлагают системы уравнений с тремя неизвестными, хотя встречаются и с другим количеством. Если в уравнении будет две неизвестные, то формулы Крамера будет только две: для х и y; если четыре неизвестные, то формулы Крамера будет четыре: x,y,z и, например, g. Кстати, в уравнениях могут быть и другие переменные, a,b,c,d... алфавит то большой.

Давайте разберемся, что делать дальше с этими формулами.

Давайте сначала обратимся к знаменателю: там во всех формулах стоит одно и то же - ∆. В статье определитель матрицы, я уже рассказывала о том, как обозначают определители. Итак, знаменатель формулы - это определитель основной матрицы, которую составляют из коэффициентов системы уравнений.

Давайте на примере системы уравнений составим определитель основной матрицы:

Для этого выписываем коэффициенты: первое уравнение системы имеет при переменной х коэффициент 1, при y - коэффициент -1, при z - коэффициент 2. Записываем все эти коэффициенты в первую строку определителя основной матрицы, коэффициенты второго уравнения во вторую строку (обратите внимание второе уравнение не содержит переменной z, значит во второй строке определителя на третьем месте ставим ноль, коэффициенты третьего уравнения - в третью строку. Определитель готов. Следующий шаг: рассчитать определитель по формуле Саррюса или по теореме Лапласа.

Мы воспользуемся формулой Саррюса или правилом треугольника:

Важно: определитель не должен равняться нулю, т.к. в формулах Крамера он стоит в знаменателе, а как известно всем, на ноль делить нельзя!

В нашем случае он равен 17, значит переходим к следующему шагу.

Теперь найдем: ∆_х. Для этого в столбец, где стоит переменная х, а значит в первый столбец, вместо коэффициентов при х, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений:

Аналогично найдем ∆_y. Для этого в столбец, где стоит переменная y, а значит во второй столбец, вместо коэффициентов при y, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений:

Аналогично найдем ∆z_. Для этого в столбец, где стоит переменная z, а значит втретий столбец, вместо коэффициентов при z, ставим свободные коэффициенты, которые в системе уравнений стоят в правых частях уравнений:

Ну вот и нашли все что необходимо знать в формулах Крамера. Остается подставить найденное в эти формулы:

решение системы уравнений методом обратной матрицы.

Для использования этого метода необходимо уметь находить обратную матрицу. Более подробно об этом я уже писала в статье "Обратная матрица".

Сейчас разберем алгоритм решения системы уравнений, используя метод обратной матрицы:

1. Данную систему уравнений необходимо записать в матричной форме:

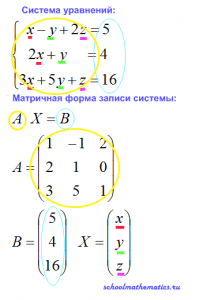
2. Выразить неизвестные переменные:

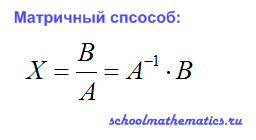
Мы видим, что решение матричным способом сводится к умножению обратной матрицы к матрице А на матрицу свободных членов. т.е. матрицу В. Вот на этом то этапе нам и нужны навыки нахождения обратной матрицы.

3. Итак, найдем матрицу обратную матрице А:

Сначала рассчитаем определитель основной матрицы:

Определитель не равен нулю, значит обратная матрица существует. Найдем 9 дополнений матрицы:

Для первой строки:

Для второй строки:

Для третьей строки:

4. Составим обратную матрицу:

5. Вернемся к матричной форме записи системы уравнений и выраженным неизвестным, подставим в эту форму полученные данные:

6. Остается перемножить две матрицы:

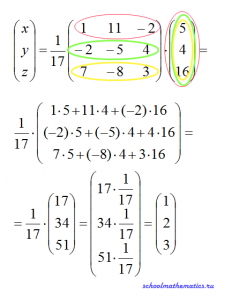
Итак, метод обратной матрицы привел нас к ответу: x=1, y=2, z=3.

Алгоритм нахождения нормы матрицы я и приведу. Ну во первых норма матрицы - это всегда какое-либо число. Выделяют всего три нормы матрицы:

1 норма матрицы представляет из себя максимальное из чисел, полученных при сложении всех элементов каждого столбца, взятых по модулю. Не путайте со сложением матриц!

Рассмотрим на примере: пусть дана матрица размера 3х2. В первом столбце стоят элементы: 8, 3, 8. Все элементы положительные. Найдем их сумму: 8+3+8=19. В втором столбце стоят элементы: 8, -2, -8. Два элемента - отрицательные, поэтому при сложении этих чисел, необходимо подставлять модуль этих чисел (т.е. без знаков "минус"). Найдем их сумму: 8+2+8=18. Максимальное из этих двух чисел - это 19. Значит первая норма матрицы равна 19.

2 норма матрицы представляет из себя квадратный корень из суммы квадратов всех элементов матрицы. А это значит мы возводим в квадрат все элементы матрицы, затем складываем полученные значения и из результата извлекаем квадратный корень.

В нашем случае, 2 норма матрицы получилась равна квадратному корню из 269. На схеме, я приближенно извлекла квадратный корень из 269 и в результате получила приблизительно около 16,401. Хотя более правильно не извлекать корень.

3 норма матрицы представляет из себя максимальное из чисел, полученных при сложении всех элементов каждой строки, взятых по модулю.

В нашем примере: в первой строке стоят элементы: 8, 8. Все элементы положительные. Найдем их сумму: 8+8=16. В второй строке стоят элементы: 3, -2. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 3+2=5. В третьей строке стоят элементы 8, и -8. Один из элементов отрицательный, поэтому при сложении этих чисел, необходимо подставлять модуль этого числа. Найдем их сумму: 8+8=16. Максимальное из этих трех чисел - это 16. Значит третья норма матрицы равна 16.

Как мне сложить две матрицы?

Правило сложения двух матриц: «добавь строку и колонку к строке и колонке».

Математически это выглядит так:

При этом матрицы должны быть одного размера. К примеру, если матрица 3x3 M складывается с матрицей 3x3 L результат будет таким: .

Как мне вычесть две матрицы?

Правило вычитания двух матриц: «вычитай строку и колонку из строки и колонки».

Математически будет так:

Матрицы должны быть строго одного размера.

К примеру, если матрица 3x3 L вычитается из матрицы 3x3 M результат будет таким: .

Как мне умножить две матрицы?

Правило такое: «умножай строку на колонку и сумма будет результатом.»

Математически:

Если есть две матрицы: и

то величины B и C должны быть равны.

Результат будет

Так что, можно умножить матрицу 4xN с матрицей 4x4, но не наоборот.

К примеру, если матрица 4x4 M описана 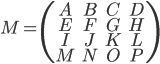так: и матрица 4x2 L описана так:

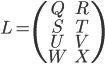
то размер результата будет 2x4:

Как мне взять корень или возвести матрицу в квадрат?

Из матрицы можно взять корень или возвести в целую степень. Однако есть несколько ограничений. Для любого возведения матрица должна быть квадратная, иначе говоря, количество столбцов должо быть равно количеству строк.

К примеру, — обратная матрица,

— единичная матрица,

— матрица не меняется,

— возводит в квадрат,

— куб матрицы.

Возведение матрицы в степень больше одного означает умножить матрицу на себя n-число раз.

К примеру:

и так далее.

Возведение в степень единичной матрицы всегда даёт единичную матрицу:

Как мне умножить один и более векторов на матрицу?

Лучший способ выполнить это задание представить список векторов в виде одной матрицы, где каждый вектор представлен одной колонкой.

Если N векторов должны быть умножены на матрицу 4х4, они могут быть выражены в виде одной матрицы 4хN: а список векторов:

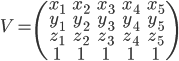
Заметьте, что вся дополнительная четвертая строка равна константе 1. Она не играет никакой роли, используется, чтобы порядок матрицы M совпадал с порядком списка V. Умножение производится так:

На каждый вектор в списке приходится в общем 12 умножений, 16 сложений и 1 деление для перспективы. Если известно, что это матрица поворота или переноса, то можно не делить.

Определитель и обратная матрица

Что такое определитель матрицы?

Определитель матрицы это число, которое показывает, есть ли у матрицы обратная или нет. Если определитель равен 0, то обратной матрицы нет, иначе обратная матрица существует.

К примеру, есть матрица из одного элемента: . Для матрицы такого размера, определитель это просто значение одного элемента. А, обратная матрица: .

Если элемент, а соответственно и определитель, не равен 0, то обратная матрица существует.

В случае единичной матрицы ее значение будет 1/1 или 1.0 Однако, если это число 0, то и определитель тоже 0. При попытке найти обратное от нуля, получаем бесконечность. Так делать нельзя, так что для 0 не существует обратной матрицы.

Для единичной матрицы определитель всегда равен 1. Все матрицы с определителем равным единице называют изотропными.

Поэтому все матрицы вращения изотропны, так как определитель всегда равен 1.0.

Что можно доказать так: но мы знаем, что: Так что

Как мне посчитать определитель матрицы?

Определитель матрицы считается при помощи правила Крамера, где каждое число может быть рассчитано через разбиение матрицы в более малые матрицы.

Для 2х2 матрицы М, определитель В считается так:

Для матриц размером 3х3 и 4х4, найти определитель сложнее, но все равно можно при помощи методов типа правила Крамера.

Что такое изотропная и анизотропная матрицы?

Изотропной матрицей называют матрицу, в которой сумма квадратов всех трех строк или колонок равна 1.

Матрицы, в которой это не происходит, называется Анизотропной.

Матрицы используются для того, чтобы поворачивать и скалировать объект, иногда может быть необходимо, увеличивать или сжимать по одной оси сильнее, чем по другим.

К примеру, в сейсмических задачах, необходимо увеличить ось Z на 50 или более, при этом оси X и Y нужно оставить неизменными.

Другим примером может служить «раздавливание» и «растягивание» в анимации персонажей. Когда персонаж ударяет тяжелый предмет типа наковальни, то необходим эффект, при котором персонаж растягивается в стороны и сдавливается вертикально:

Матрица будет выглядеть так:

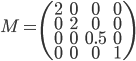
Однако здесь появляется проблема. В то время как не будет проблем с обработкой вершин, мы получим неправильное освещение, из-за кривых нормалей.

На шаге обработки данных, трансформация, выраженная данной матрицей Изменит как вершины, так и нормали.

После такого умножения, все нормали перестанут быть нормализованными, что подействует на освещение и обратное отсечение.

Что такое обратная матрица?

Дана матрица , то обратная матрица этой матрицы, записывается как M, это матрица должна удовлетворять условию:

где I единичная матрица.

Так что, в результате умножения матрицы на обратную к ней будет единичная матрица. Однако матрица должна удовлетворять нескольким условиям, перед тем как обратная матрица будет посчитана.

Во-первых, ширина и высота матрицы должны совпадать, во-вторых ее определитель не должен равняться 0.

Расчет обратной матрицы необходим для реализации обратной кинематики с помощью сплайнов.

Как мне посчитать обратную матрицу?

В зависимости от размера матрицы, расчет обратной может быть простым или очень сложным.

К примеру, обратная 1х1 матрица это просто обратная от одного элемента:

Обратная матрица:

.

Решение 2х2 матриц и больших может быть получено при использовании правила Крамера или через решение системы уравнений.

Однако, для конкретных случаев, таких как единичная матрица или матрицы поворота, обратная матрица сразу известна или может быть получена транспонированием.

Как мне посчитать обратную матрицу от единичной матрицы?

Обратная единичной матрицы и есть единичная матрица. У любой единичной матрицы определитель всегда равен 1.