Законы Кирхгофа

Законы Кирхгофа являются формальными правилами, упрощающими расчет разветвленных электрических цепей. Первый закон Кирхгофа касается узловых токов. Узлами электрической цепи называются точки, в которых сходятся более чем два элемента цепи. Пусть в узел втекают и из него вытекают несколько токов. Согласно закону сохранения заряда, суммарный заряд, вошедший в узел за некоторое время, должен быть равен суммарному заряду, вышедшему из узла за это же время. Отсюда следует, что суммарная сила тока, втекающего в узел, равна суммарной силе тока, вытекающего из узла:

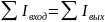
Э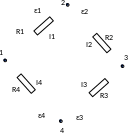 тот факт называется первым законом Кирхгофа.

Второй закон Кирхгофа касается замкнутых контуров. Выделим в разветвленной цепи некоторый замкнутый контур. Рассмотрим, например, контур, представленный на рисунке. Обозначим узлы контура и расставим (произвольно) направления токов в участках контура. Запишем Закон Ома для каждого участка контура:

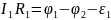
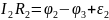
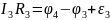
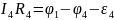
Выберем направление обхода контура (например, по часовой стрелке) и перепишем уравнения таким образом, чтобы разность потенциалов соответствовала направлению обхода, то есть, чтобы она записывалась так: 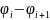. В записанных нами уравнениях надо переписать третье и четвертое:

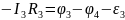
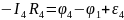
Сложив полученные уравнения, получим:

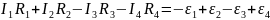
Полученное уравнение по сути и есть второй закон Кирхгофа: алгебраическая сумма падений напряжения на всех сопротивлениях замкнутого контура равна алгебраической сумме всех ЭДС, действующих в контуре. При этом слагаемое считается положительным, если направление тока в сопротивлении совпадает с направлением обхода или если ЭДС проходится в прямом направлении, то есть от минуса к плюсу. В противном случае слагаемое считается отрицательным.

Пусть имеется электрическая цепь. Если в цепи имеется n узлов, то первый закон Кирхгофа можно записать для n – 1 узлов. Если записать еще второй закон Кирхгофа для всех независимых контуров цепи, то получается система уравнений, достаточная для нахождения силы тока во всех элементах цепи.

Соединение источников ЭДС

Иногда в задачах встречаются схемы, содержащие несколько источников ЭДС. Если источники соединены друг с другом последовательно или параллельно, то часто схему можно упростить, заменив несколько источников одним эквивалентным. Приведем без доказательства.

П усть несколько источников, имеющих ЭДС ε₁, ε₂, ε₃, … и внутренние сопротивления r₁, r₂, r₃, … соединены последовательно. Их можно заменить одним источником, ЭДС которого равна:

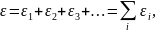
а внутреннее сопротивление:

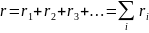
При этом следует иметь в виду, что первая сумма является алгебраической, то есть слагаемые в ней могут быть как положительными, так и отрицательными в зависимости от полярности включения каждого источника. Например, для приведенного на рисунке участка цепи надо написать:

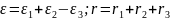
Пусть несколько источников, имеющих ЭДС ε₁, ε₂, ε₃, … и внутренние сопротивления r₁, r₂, r₃, … соединены параллельно. Их можно заменить одним источником, внутреннее сопротивление которого определяется по формуле:

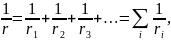
а ЭДС:

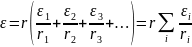
Вторая из приведенных сумм тоже является алгебраической.

Строго говоря, понятием эквивалентного источника можно пользоваться только в задачах, связанных с расчетом силы тока в цепи. В задачах, связанных с расчетом мощности источников тока, замена исходной системы источников одним эквивалентным может привести к ошибкам.