Теоретичні положення

Напруженість магнітного поля у будь-якій точці циліндричної котушки може бути визначена експериментальним і аналітичним шляхом. Розглянемо методику розрахунку напруженості магнітного поля на осі циліндричної котушки без магнітопроводу.

Сумістимо вісь OX з віссю котушки і розташуємо початок координат у центрі котушки. Для наближеного розрахунку напруженості на осі котушки замінимо реальну багатошарову котушку одношаровою з тією ж кількістю витків, з тією ж довжиною і з тим же радіусом витків, який дорівнює середньому радіусу витків реальної котушки.

Напруженість магнітного поля на осі котушки вираховуємо за законом Біо-Савара-Лапласа. Відповідно цьому закону струм I, який про­ходить по лінійному провіднику довжиною , створює магнітне поле, яке у точці, віддаленій від елемента на відстань r, має напруженість

, ( 23.1 )

де : - радіус – вектор направлений від елемента струму до точки, в якій визначається напруженість.

Модуль вектора визначається з виразу

, ( 23.2 )

де : - кут між векторами та .

Вектор перпендикулярний до та радіус-вектора і напрямлений у той бік , який визначається правилом правого гвинта .

Спочатку знайдемо напруженість магнітного поля у точці , яка

лежить на осі колового витка, по котрому тече струм І ( рис. 23.1 ).

Н ехай - радіус витка. Для точок, що лежать на осі витка, і , тоді :

( 23.3 )

Рисунок 23.1.

Кожні два рівних елементи витка і , що лежать на протилеж­них кінцях діаметра витка, обумовлюють у точці вектори і , складові яких нормальні до осі ОХ, взаємно компенсуються. Навпаки, складові цих векторів, що направлені вздовж осі ОХ, складаються. Отже виходить, що при обчислені напруженості магнітного поля у точці , обумовленої струмом у всьому витку, достатньо врахувати тільки складову кожного елементарного вектора , що направлена вздовж вісі ОХ, яка дорівнює , де - кут між віссю ОХ і радіус-вектором .

Інтегруючи вираз ( 23.3 ) вздовж всього витка, одержимо формулу для напруженості магнітного поля на осі колового витка

. ( 23.4 )

Оскільки , тоді ( 23.5 )

В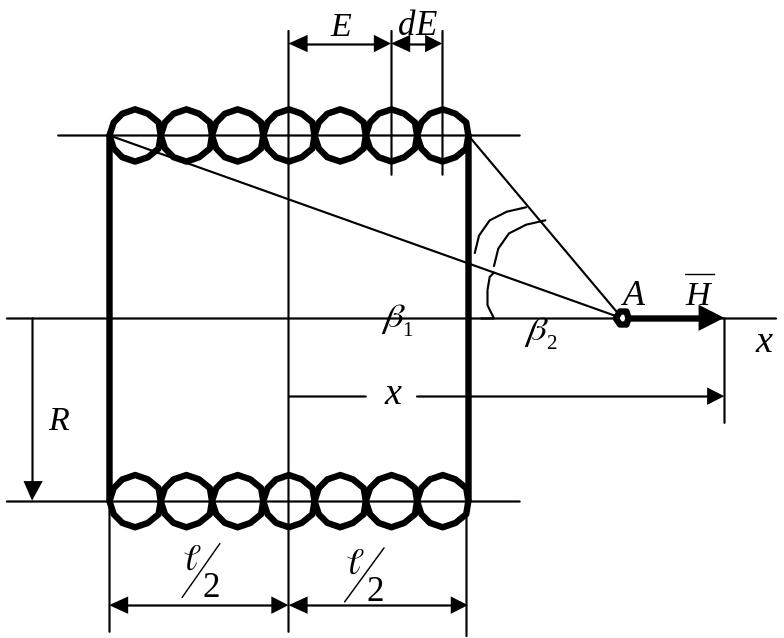 икористовуючи вираз ( 23.5), знайдемо напруженість маг­ніт­ного поля у точці , яка лежить на осі одношарової котушки, яка має довжину , число витків і радіус витків R ( рис. 23.2 ).

Виділимо елемент довжини котушки . Його можна розглядати як дуже тонкий коловий контур зі струмом

Рисунок 23.2 . ( 23.6 )

Відповідно з ( 23.5 ), напруженість магнітного поля, яка буде викликана цим струмом становить

( 23.7 )

Напруженість у точці , що створюється струмом всієї котушки, знайдемо інтегруванням виразу ( 23.7 ) по довжині всієї котушки , тобто :

,

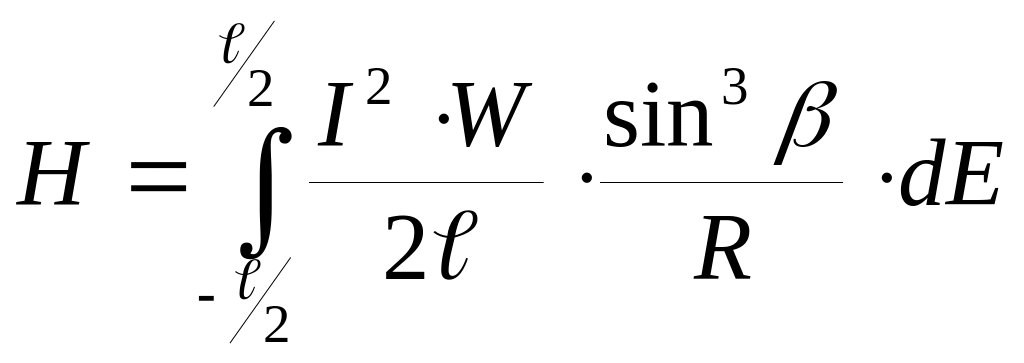де , тоді .

Таким чином

. ( 23.8 )

де: , - крайні значення , які відповідають краям котушки ( рис.23.2 ).

Косинуси цих кутів можна визначити за формулами :

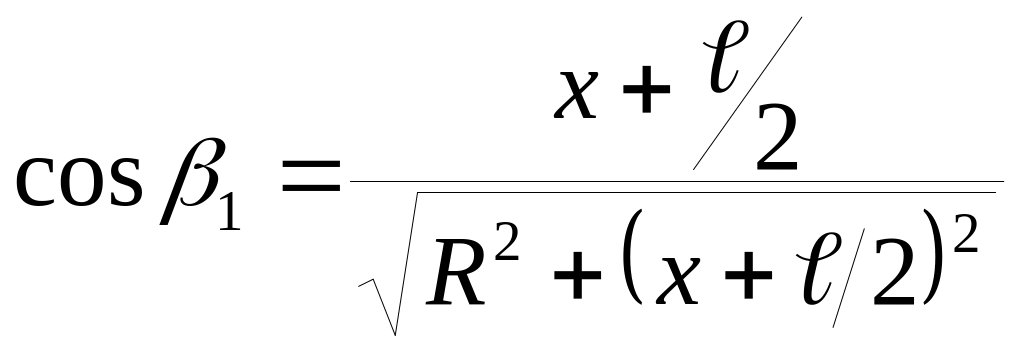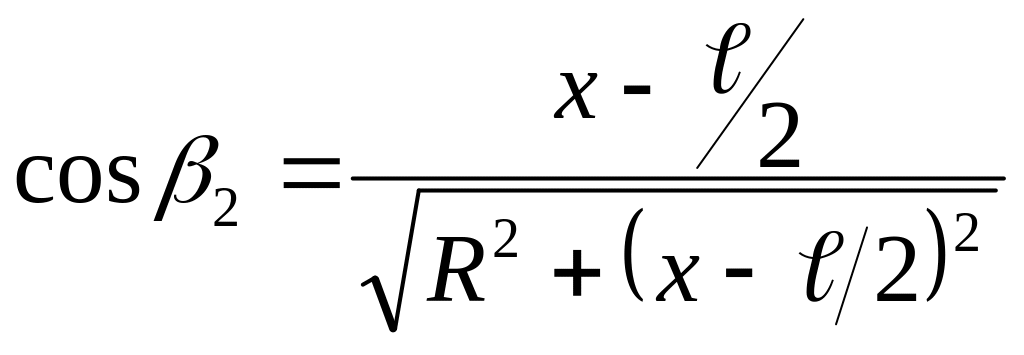, ( 23.9 )

де: - відстань точки до середини котушки .