2. Сложение матриц.
Операция сложения вводиться только для матриц одинакового размера.
ОПРЕДЕЛЕНИЕ:
Суммой
двух матриц
и
одинакового размера
и
,
называется матрица
,
элементы которой
,
для
;
.(т.
е матрицы складываются поэлементно).
3. Вычитание матриц.
Разность двух матриц одинакового размера определяется через предыдущие операции:
ОПЕРАЦИИ СЛОЖЕНИЯ И УМНОЖЕНИЯ ОБЛАДАЮТ СЛЕДУЮЩИМИ СВОЙСТВАМИ:
1.
-
коммутативность. 5.
2.
-ассоциативность
6.
3.
7.
4.
8.
Где
-
матрицы,
и
-
числа.
4. Умножение матриц
Операция умножения двух матриц определена только тогда, когда число столбцов первой матрицы равно числу строк второй матрицы.
ОПРЕДЕЛЕНИЕ:
Произведением
матриц
называется такая матрица
,
каждый элемент которой
равен сумме произведений элементов
-
строки матрицы
на соответствующие элементы
-
столбца матрицы
.
,
где
.
ПРИМЕРЫ: 1) Вычислить произведение матриц:
и
.
Можно ли умножить матрицу на матрицу ? Нет, так как число столбцов матрицы не равно числу строк матрицы , но можно умножить на .
.
В этом примере
наглядно видно одно
из специфических свойств
операции умножения двух матриц. Если
не существует
,
то
может и существовать.
2) Вычислить произведение матриц:
Решение: число столбцов и число строк обеих матриц равно.
;
.
;
,
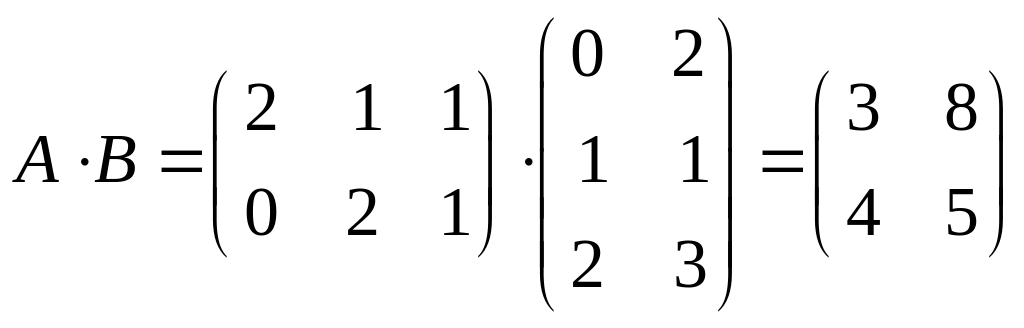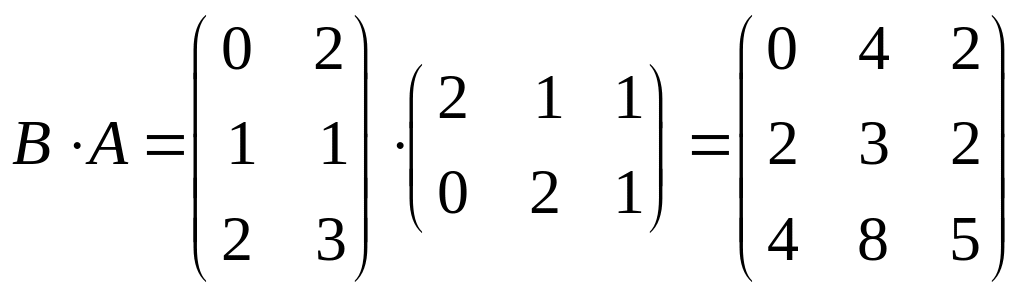таким образом, получаем, что
.
На этом примере продемонстрировано
второе
специфическое свойство операции
умножения матриц: если даже произведения
и
существуют, то они могут быть матрицами
разного размера.
3 специфическое свойство: В случае, когда оба произведения и существуют и обе матрицы одинакового размера (это возможно только при умножении квадратных матриц и одного порядка), коммутативный закон умножения не выполняется, т.е. .
ПРИМЕР: Найти
произведения матриц
.
;
,
т.е.
В частном случае коммутативным законом обладает произведение любой квадратной матрицы - порядка на единичную матрицу того же порядка, причем это произведение равно .
.
ПРИМЕР: Пусть
,
тогда
4
специфическое
свойство: Произведение
двух ненулевых матриц
может
равняться нулевой матрице. Т.е. если
,
то это не значит, что
или
.
ПРИМЕР:
,
но
.
5. Возведение в степень
ОПРЕДЕЛЕНИЕ:
Целой
положительной степенью
квадратной матрицы
называется произведение
матриц, равных
,
т.е.
.
Операция возведения в степень определяется только для квадратных матриц.
По определению
полагают
.
ПРИМЕР:
Найти
,
.
РЕШЕНИЕ:
ЗАМЕЧАНИЕ: Из
равенства
еще не следует, что матрица
.
6. Транспонирование матрицы
ОПРЕДЕЛЕНИЕ:
Матрица,
полученная из данной, заменой каждой
ее строки столбцом с тем же номером
называется транспонированной к данной.
Обозначается
.
ПРИМЕР:
тогда
;
если
,
тогда
;