4.2. Моделирование алгоритма сложения двоичных чисел

Числа в ЭВМ могут быть представлены в форме с фиксированной запятой или в форме с плавающей запятой [5].

Для сложения чисел с фиксированной запятой надо лишь выполнить поразрядное сложение в двоичной системе счисления с учетом переносов.

При сложении чисел одинакового знака может произойти переполнение разрядной сетки. Для его выявления в знаковую часть изображения числа вводится вспомогательный разряд, называемый разрядом переполнения. Такое представление числа называется модифицированным. Если значения знаковых разрядов числа в модифицированном коде не совпадают (зн[1] ≠ зн[2]), то делают вывод о переполнении.

Если переполнение разрядной сетки возникло при сложении чисел с плавающей запятой, то производится нормализация числа вправо. Нормализация производится также в том случае, если модуль мантиссы меньше ½, но число при этом нормализуется влево. Различные случаи ненормализованных мантисс приведены в табл. 4.1.

Таблица 4.1

Различные случаи ненормализованных мантисс

Разряды мантиссы	Величина мантиссы	Действия, выполняемые для нормализации результата
01, хх…х	Мантисса больше либо равна единице	Сдвиг мантиссы вправо на один разряд, увеличение порядка на единицу
10, хх…х
00,00…0хх…х k - разрядов	Модуль мантиссы меньше 1/2	Сдвиг мантиссы влево на k разрядов, уменьшение порядка на k единиц
11,11…1хх…х k – разрядов

Схема алгоритма сложения чисел с плавающей запятой представлена на рис. 4.2. В ней использованы обозначения: n - количество разрядов мантиссы, k – число разрядов порядка, М₁, М₂ – мантиссы и Р_1, Р₂ - порядки чисел.

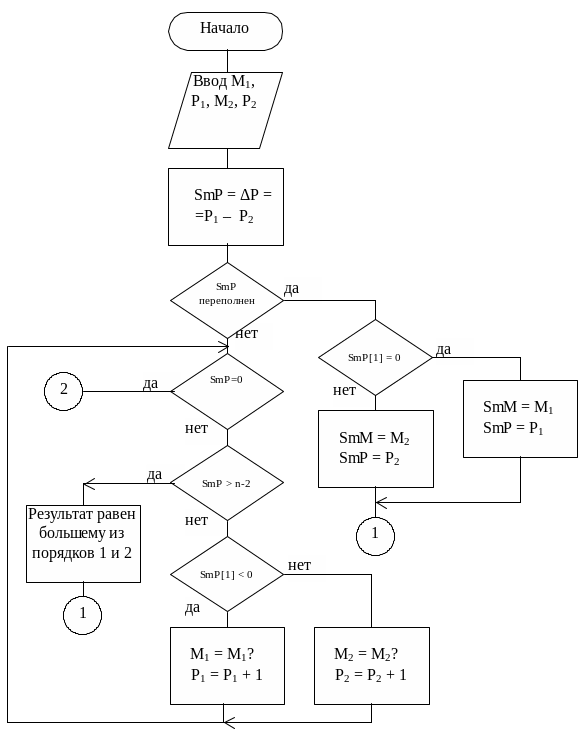
Рис. 4.2. Схема алгоритма сложения чисел с плавающей запятой

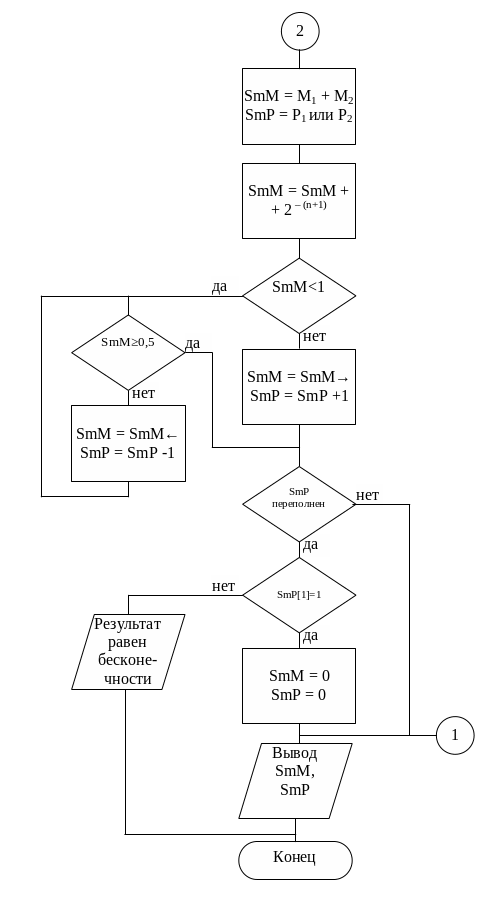
Рис. 4.2. Схема алгоритма сложения чисел с плавающей запятой

(окончание)

Сложение мантисс выполняется на сумматоре мантисс SmM и возможно только при одинаковых порядках чисел. В связи с этим сначала нужно выровнять порядки, для чего на сумматоре порядков SmP определяется разность Δ Р = Р₁ – Р₂. Если ΔР = 0, то порядки равны (P₁ = Р₂) и возможно сложение мантисс. При ΔР>0 первое число больше второго, и мантисса второго числа должна быть сдвинута на ΔР разрядов вправо. В случае ΔР<0 второе число больше первого. Следовательно, для выравнивания порядков необходимо сдвинуть на |ΔР| разрядов вправо мантиссу первого числа. Если |ΔР| превосходит количество цифровых разрядов, то в качестве результата операции сложения принимается большее число.

При нахождении разности порядков может иметь место переполнение результата (SmP). Если переполнение положительное, то в качестве результата сложения должен быть принят первый операнд. Отрицательное переполнение сумматора порядков свидетельствует о том, что в качестве результата сложения должен быть принят второй операнд.

После выполнения сложения мантисс может получиться денормализованный результат. При нормализации результата меняется величина порядка. Также может иметь место переполнение сумматора порядков. В случае положительного переполнения результат считается бесконечностью, знак которой определяется знаком мантиссы. При отрицательном переполнении сумматора порядков считается, что получен бесконечно малый результат, заведомо отличный от нуля, если мантисса не равна нулю.

Поскольку при выравнивании порядков мантисса меньшего из чисел сдвигается вправо, то имеет место потеря ее цифровых разрядов. В этом случае сумма чисел получается с недостатком, и для исключения накопления ошибок вычислений производится округление, для чего в сумматор вводится дополнительный младший разряд, к которому после выполнения операции сложения добавляется единица.