2.2. Сложение (вычитание) двоичных чисел с плавающей запятой
Выше уже отмечалось, что при вычислительных операциях с плавающей запятой двоичные числа представляются в виде мантиссы с ее знаком, которая по модулю строго меньше единицы, и порядка с его знаком, который может быть равен нулю или любому (в пределах отведенного числа разрядов) целому числу, т.е. .
Операция сложения (вычитания) чисел с плавающей запятой производится следующим образом.
Первоначально уравнивают порядки слагаемых, для того чтобы привести в соответствие весовые коэффициенты одноименных разрядов мантисс слагаемых. Для этого меньший порядок слагаемого увеличивают до значения, равного большему порядку, а мантиссу этого слагаемого денормализуют, т.е. сдвигают вправо на число разрядов, равное разности между большим и меньшим порядками слагаемых.
Затем мантиссы обоих слагаемых переводят в модифицированный обратный или в модифицированный дополнительный код с учетом их знаков и складывают в соответствующем коде по рассмотренным выше правилам сложения чисел с фиксированной запятой. При этом возможны три случая.
Первый случай. Сложение мантисс слагаемых произошло без переполнения разрядной сетки и нарушения нормализации.
В этом случае результат сложения мантисс переводится из модифицированного обратного (дополнительного) кода в прямой код и представляется как мантисса суммы. Порядком суммы при этом является общий после уравнивания порядок слагаемых.
Второй случай. Сложение мантисс слагаемых произошло без переполнения разрядной сетки, но результат после перевода мантиссы суммы в прямой код оказался ненормализованным.
В этом случае производится нормализация результата сложения, т.е. мантисса суммы сдвигается на соответствующее число разрядов влево, а порядок суммы уменьшается на такое же число.
Третий случай. При сложении мантисс слагаемых произошло переполнение разрядной сетки, т.е. в знаковых разрядах мантиссы суммы оказалась комбинация 01 или 10.
В этом случае цифры всех разрядов данной мантиссы суммы, включая знаковые, сдвигаются на один разряд вправо, после чего в старший знаковый разряд заносится цифра, совпадающая с цифрой, оказавшейся в младшем знаковом разряде после сдвига. Полученный таким образом результат переводится в прямой код и представляет собой мантиссу суммы. Порядок же суммы при этом следует увеличить, и он будет на единицу больше значения уравненных порядков слагаемых.
Пример (первый случай).
Слагаемые:
Требуется
найти
,
т.е найти
и
.
Первый шаг.
Уравнивание порядков слагаемых, т.е. денормализация слагаемого , чтобы его порядок стал равен + 101.
После
уравнивания
.
Второй шаг.
Перевод мантисс обоих слагаемых в модифицированный обратный код
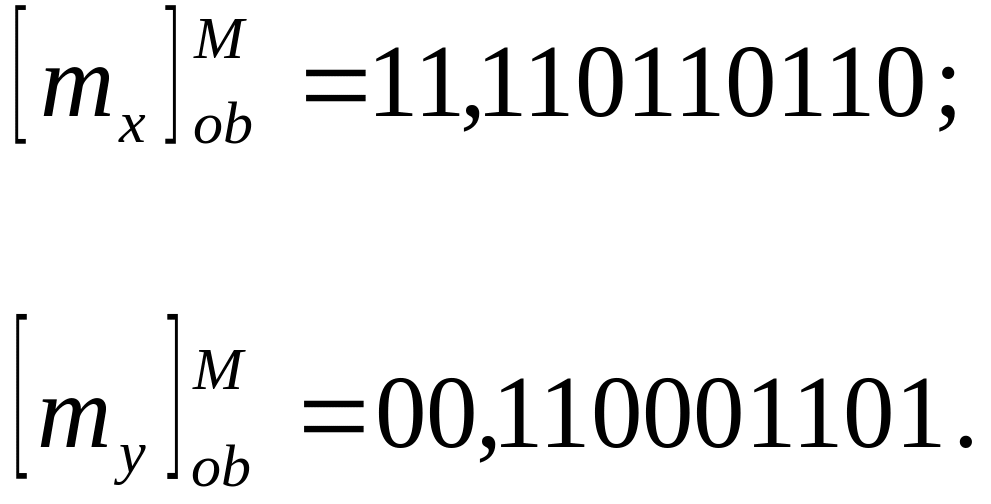
Третий шаг.
Сложение мантисс
1
+
.
Четвертый шаг.
Перевод
мантиссы суммы в прямой код
.
Результат
операции сложения
.
Пример (второй случай).
Слагаемые: 
Требуется найти , т.е найти и .
Будем производить вычисление в модифицированном обратном коде.
Уравнение порядков в данном примере не требуется.
Первый шаг.
Перевод мантисс слагаемых в модифицированный обратный код
Второй шаг.
С
ложение
мантисс слагаемых 
Третий шаг.
Перевод мантиссы суммы в прямой код
.
Произошла денормализация вправо на три разряда.
Четвертый шаг.
Устранение денормализации путем сдвига прямого кода мантиссы суммы на три разряда влево и вычитания из первоначального порядка суммы трех единиц. Вычитание производится в модифицированном дополнительном или в модифицированном обратном коде
Результат операции сложения
Пример (третий случай).
Слагаемые: 
Требуется
найти
,
т.е найти
и
.
Будем производить вычисления в модифицированном обратном коде.
Первый шаг.
Уравнение порядков слагаемых
.
Второй шаг.
Перевод мантисс слагаемых в модифицированный обратный код
Третий шаг.
Сложение мантисс слагаемых
1
+
10,111011110
Произошло переполнение разрядной сетки (денормализация влево), т.к. в знаковых разрядах мантиссы суммы оказались разные знаки.
Четвертый шаг.
Устранение переполнения (нормализация) путем сдвига мантиссы суммы на один разряд вправо и прибавления единицы к первоначально полученному порядку суммы в модифицированном дополнительном или в модифицированном обратном коде.
Пятый шаг.
Перевод мантиссы суммы в прямой код
Результат
операции сложения
