2.2 Задачи на использование комбинаторики при подсчёте вероятностей

Задача 2.2.1

В розыгрыше первенства по баскетболу участвуют 18 команд, из которых случайным образом формируются две группы по 9 команд в каждой. Среди участников соревнований 5 команд экстра-класса. Найти вероятность того, что в одну из групп попадут две команды экстра-класса, а в другую – три.

Решение:

Р ассмотрим события:

А - в одну из групп попадут две команды экстра-класса, а в другую – три,

А₁ - в первую группу попадут две команды экстра-класса,

А₂ - во вторую группу попадут две команды экстра-класса.

Так как А = А₁ + А₂ и события А₁ и А₂ несовместны, то по формуле (10) получим: .

Пусть n – общее число случаев, m₁ - число случаев, благоприятствующих событию А₁, тогда, по формуле (1), . Так как при выборе команд, их последовательность в выборке не важна, для нахождения n и m₁ используем число сочетаний (4):

Ответ: вероятность того, что в одну из групп попадут две команды экстра-класса, а в другую – три, равна 0,71.

2.3 Задачи на формулу полной вероятности и формулу Байеса

Задача 2.3.1

Из урны, содержащей 3 белых и 2 чёрных шара, переложены два вынутых наудачу шара в урну, содержащую 4 белых и 4 чёрных шара. Найти вероятность вынуть из второй урны белый шар. Какова вероятность того, что шар, случайным образом вынутый из второй урны, оказавшись белым, не был переложен в неё из первой урны?

Решение:

Рассмотрим гипотезы:

H₁ – из первой урны вынуты два белых шара,

H₂ – из первой урны вынуты два чёрных шара,

H₃ – из первой урны вынуты белый и чёрный шары.

Н айдём вероятности гипотез. Так как в первой урне было 5 шаров, а вынули из неё 2 шара, то общее число случаев вынуть два шара из пяти равно . Число случаев, благоприятствующих H₁, равно , тогда .

Аналогично, 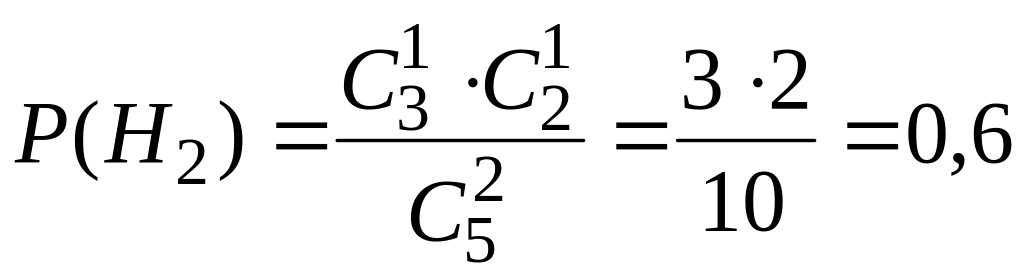и

Так как гипотезы образуют полную группу событий, должно выполняться:

(что и получим, так как ).

По формуле полной вероятности (14) найдём вероятность события А, которое заключается в том, что из второй урны будет вынут белый шар:

.

Найдём условные вероятности событий . События означают: из второй урны вынут белый шар при условии, что из первой вынули соответствующую i – той гипотезе комбинацию шаров. Так, при осуществлении H₁ во второй урне окажется 10 шаров, среди которых будет 6 белых. Тогда .

Аналогично, и

Окончательно получим:

Найдем вероятность того, что шар, случайным образом вынутый из второй урны, оказавшись белым, находился в ней изначально. В этом случае имела место только гипотеза . Для ответа на вопрос потребуется найти условную вероятность гипотезы при условии, что произошло событие А. По формуле Байеса (15) получим:

Ответ: вероятность того, что из второй урны вынут белый шар, равна 0,52; вероятность того, что шар, вынутый из второй урны, оказавшись белым, не был переложен в неё из первой урны, равна 0,57.

2.4 Вычисление вероятности наступления события в серии n независимых испытаний

Задача 2.4.1

Владельцы кредитных карточек теряют их весьма редко. Вероятность потери карточки для любого из них равна 0,001. Найти вероятность того, что из 200 владельцев потеряют карточку:

а) три владельца;

б ) более двух владельцев.

Решение:

а) Рассмотрим события:

А – один из 200 человек потерял карточку,

В – трое из 200 человек потеряли карточку. В заключается в том, что в серии из 200 независимых испытаний событие А должно произойти три раза (m = 3).

В каждом из этих испытаний событие А появляется с постоянной вероятностью р = 0,001 и не появляется с вероятностью q (q=1–0,001=0,999). Так как p мала, n велико и события (потеря карточки первым, вторым и третьим владельцами) независимы, при отыскании Р(В) используем формулу Пуассона (21):

.

Получаем:

б) Пусть событие С заключается в том, что более двух владельцев потеряют карточку. Тогда событие (карточку потеряют не более двух владельцев) означает, что карточку потеряют 0, 1 или 2 владельца. Тогда

Ответ: вероятность того, что а) трое из 200 владельцев потеряют карточку равна 0,00109; б) более двух владельцев – 0,00114 (т.е. в обоих случаях около 0,1%).

Задача 2.4.2

Среди пассажиров маршрута № 9 в среднем 10 из 100 – льготники. Определить

в ероятность того, что из 2000 пассажиров, проехавших за день, льготниками окажутся:

а) 180 человек;

б) от 120 до 220 пассажиров включительно.

Решение:

а) Рассмотрим события:

А - выбранный пассажир оказался льготником,

В - среди 2000 пассажиров оказалось 180 льготников.

Событие В появляется при проведении серии из n = 2000 независимых испытаний, в каждом из которых событие А происходит с постоянной вероятностью р= , при этом q = 1 – = . Так как n > 100, а npq = 180 > 20, используем локальную теорему Муавра- Лапласа (18):

где - функция Гаусса,

.

Значение функции Гаусса можно найти с помощью таблицы (Приложение Б). Так как - чётная функция, то . Тогда

б) Вероятность того, что из 2000 пассажиров льготниками окажутся от 120 до 220 пассажиров включительно, можно найти с помощью интегральной теоремы Муавра- Лапласа (20):

где (х) – функция Лапласа, значения которой можно найти с помощью таблицы (Приложение Б), при этом . Найдём значения:

Тогда

Ответ: вероятности того, что из 2000 пассажиров, проехавших за день, льготниками окажутся 180 человек и от 120 до 220 пассажиров включительно равны соответственно 1% и 93%.