Случайные функции (случайные процессы).

На практике очень часто встречаются такие случайные величины, которые зависят от времени (напряжение собственных шумов приемника, амплитуда принимаемого сигнала и т.д.). Формализация этих зависимостей осуществляется на основе случайных функций.

Случайная функция (СФ) – функция неслучайного аргумента, которая при каждом фиксированном значении аргумента является случайной величиной.

X(t)

x₁(t)

СВ (сечение)

- реализация

x₂(t)

.

m_x(t)

.

t

x_n(t)

.

t'

Сечением СФ называются СВ, соответствующая фиксированному значению аргумента.

Случайным процессом называется СФ, аргументом которой является время.

Случайные процессы различаются в зависимости от того, непрерывные или дискретные значения принимаются аргументом t случайной величины X(t).

t

Непрерывная

Дискретная

Дискретная последовательность

Дискретный процесс

Непрерывная последовательность

Непрерывный процесс

X(t)

Дискретная

Непрерывная

События

t

t₁

t₂

t₃

………

X(t)

t

X(t)

t

X(t)

t₁

t₂

t₃

………

X(t)

t

Цепь Маркова с дискретным временем

Цепь Маркова с непрерывным временем

t

t₂

t₁

t

………

Реализацией СФ называется не СФ, равной которой может оказаться СФ в результате испытания.

Характеристики сф.

Математическим ожиданием (МО) СФ X(t) называется не СФ m_X(t), которая при каждом значении аргумента t равна МО соответствующего сечения СФ:

m_X(t)= M[X(t)]

МО случайной функции - это некоторая функция, около которой варьируются конкретные значения случайных функций (конкретные реализации).

Свойства МО СФ совпадают со свойствами МО СВ.

Дисперсией СФ X(t) называется не СФ d_X(t), значение которой для каждого фиксированного значения аргумента t равно дисперсии соответствующего сечения СФ:

d_X(t)= D[X(t)]

Дисперсия характеризует разброс реализаций СФ относительно ее МО.

Свойства Дисперсии СФ совпадают со свойствами Дисперсии СВ.

Среднее квадратичное отклонение СФ X(t) – не СФ σ_x(t), которая при каждом значении аргумента t равна СФ X(t):

σ_x(t)=

МО и Дисперсия представляют собой важные характеристики функций, однако, для описания особенностей СФ их не достаточно. Для подтверждения этого рассмотрим пример:

X(t)

t

X(t)

t

t₁

t₂

t₂

1

1

x₁⁽¹⁾(t), p₁⁽¹⁾=0,5

x₂⁽²⁾(t), p₂⁽²⁾=0,5

t₁

-1

-1

x₂⁽¹⁾(t), p₂⁽¹⁾=0,5

x₁⁽²⁾(t), p₁⁽²⁾=0,5

m_x1(t₁)=0 m_x1(t₂)=0 m_x2(t₁)=0 m_x2(t₂)=0

d_x1(t₁)=1 d_x1(t₂)=1 d_x2(t₁)=1 d_x2(t₂)=1

Приведенный пример показывает, что различия внутренней структуры СФ не улавливаются.

µ

X⁽¹⁾(t₁), X⁽¹⁾(t₂)

X⁽²⁾(t₁), X⁽²⁾(t₂)

=1 µ = -1

Для описания структуры случайной функции используется корреляционная функция.

Корреляционной функцией случайной функции X(t) называется не случайная функция K_X(t, t’), которая при каждой паре значений аргументов (t, t’) равна корреляционному моменту соответствующих сечений случайной функции.

K_X(t, t’)=µ_X(t)X(t’)= M[X(t)· X(t’)]

X(t)=X(t)-m_X(t)

X(t’)=X(t’)-m_X(t’),

где X(t) и X(t’) – центрированные значения функции.

Свойства:

1. При перестановке аргументов корреляционная функция не меняется.

K_X(t, t’)= K_X(t’, t)

2. Прибавление к случайной функции X(t) не случайной функции (t) не изменяет ее корреляционной функции.

K_Y(t, t’)= K_X(t, t’)

Y(t)=X(t)+ (t)

3. Умножение случайной функции на не случайный множитель (t) обуславливает умножение корреляционной функции на производную (t)· (t’).

K_Y(t, t’)= (t)· (t’)· K_X(t, t’)

(t)= (t)· X(t)

4. Абсолютная величина корреляционной функции не превышает среднего геометрического дисперсий соответствующих сечений.

|K_X(t, t’)|≤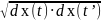

5. Зная математическое ожидание и корреляционную функцию, всегда можно найти дисперсию.

K_X(t, t)= d_X(t)