Вероятностные характеристики случайной переменной

Случайная переменная — это такая переменная, поведение которой неопределенно. А поскольку поведение не определено, то мы можем только приписывать некоторые вероятностные характеристики значениям таких переменных. Основными вероятностными характеристиками случайной переменной являются: плотность вероятности, математическое ожидание и дисперсия.

По­скольку существуют два типа случайных переменных (дискретные и непрерывные), то основные вероятностные характеристики случайной для них определяются по разному.

Плотность вероятности и распределение вероятности.

В общем случае распределение вероятностей для дискретной случайной переменной задается в следующем виде:

Значения случайной переменной			…
Вероятность			…

Непрерывная случайная переменная имеет более сложное вероятностное описание.

Опр: Функция плотности вероятности f(x) есть функция, которая для любого интервала на оси х позволяет определить вероятность того, что случайная переменная Х находится в этом интервале.

В общем случае f(x) некоторая кривая:

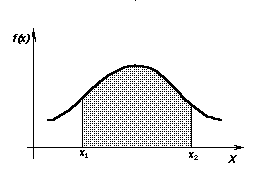
Зная функцию плотности f(x) можно определить другую функцию для случайной переменной. Для этого необходимо определить чему равна вероятность того, что случайная переменная Х примет значение не больше чем ?

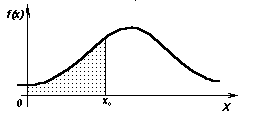
Такую вероятность можно определить для любой точки оси Х, используя интегральную функцию распределения F(x), называемую еще просто функцией распределения вероятностей: .

Отсюда следует, что вероятность попадания случайной величины Х в интервал (a; b) равна разности между значениями интегральной функции распределения в правом и левом концах интервала (a; b):

Случайные переменные, имеющие различную физическую природу, могут иметь одну и ту же вероятностную структуру, что зачастую и случается. В конечном итоге видов распределения вероятностей или, по-другому, законов распределения вероятностей не очень много. Рассмотрим некоторые из них.

Примеры законов распределения:

Первый из этих законов установил Карл Гаусс — немецкий математик 18-19 вв. Он имел дело с измерениями различных явлений и установил, что каждое такое явление несет в себе случайную ошибку измерений. Частота появления таких ошибок, если их брать в большом подчиняется определенному нормальному закону, и если отразить это на графике образуя характерную фигуру. Таким образом был сформулирован нормальный закон распределения вероятностей, согласно которому: малые отклонения от истинного результата в сторону плюса или минуса встречаются в малом числе, а истинные результаты — в большом числе (при этом, предполагается, что исключены систематические ошибки наблюдения).

Бельгийский математик А. Кетле (18-19 вв.) распространил нормальное распределение на реальные явления, а именно на измерение окружности груди шотландских солдат. Построив распределение 5738 солдат по охвату груди, он увидел, что оно сходно с распределением ошибок измерений.

Плотность вероятности нормального закона определяется по формуле: , где а и σ – постоянные, причем σ>0.

Если случайная величина Х распределена по нормальному закону распределения, то вероятность того, что Х примет значение, принадлежащее интервалу (α, β) определяется по формуле:

,

где - функция Лапласа.

Распределение Стъюдента (t-распределение с n степенями свободы). Пусть х и (хи) — независимые случайные переменные и х имеет стандартное нормальное распределение, а — -распределение с n степенями свободы. Тогда t-распределение определяется как: )

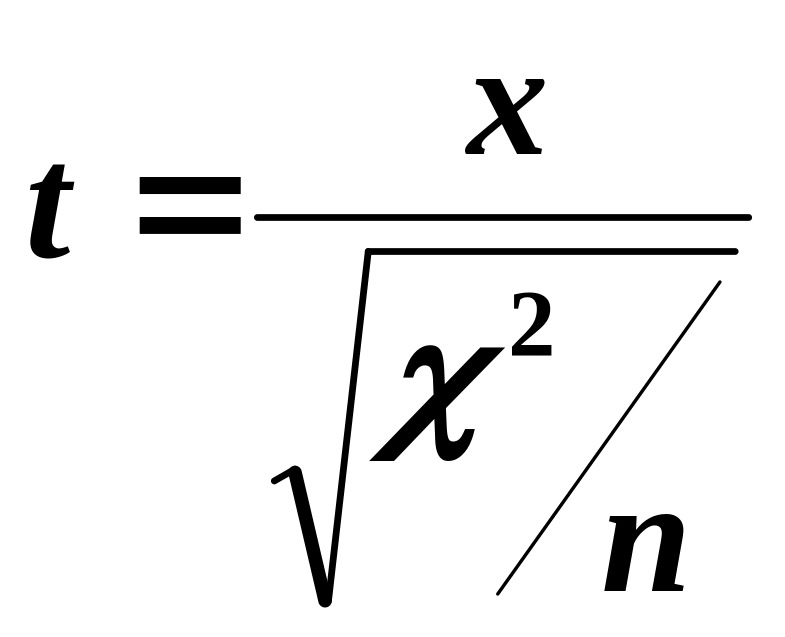Распределение Фишера (распределение F Фишера-Снедекора). Пусть и — две независимые случайные переменные имеющие -распределение со степенями свободы и . Тогда: .

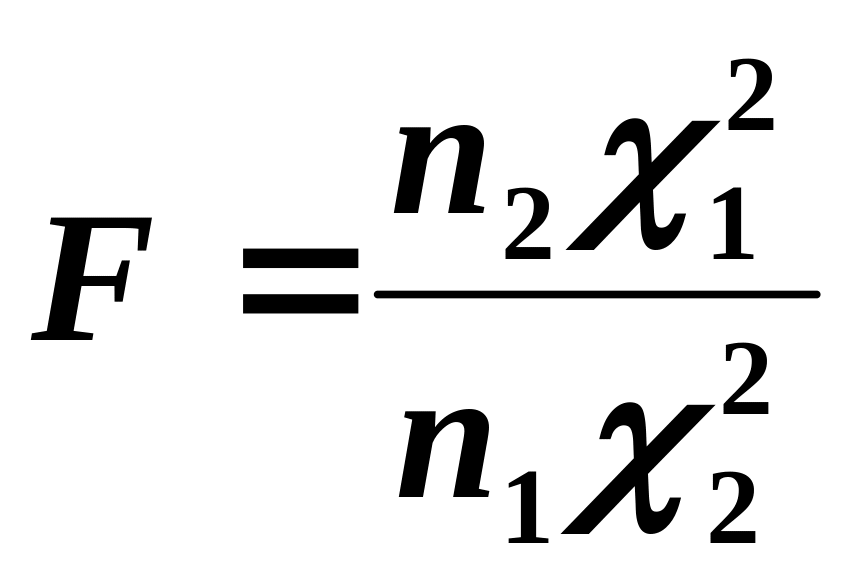Равномерное распределение.

Распределение с n-степенями свободы. Пусть Х независимая случайная переменная. Тогда: .

В учебниках и другой литературе по теории вероятностей имеются таблицы распределения вероятностей для различных законов.

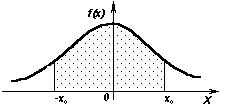
Зная плотность распределения вероятностей можно решать и обратную задачу: по заданной вероятности определить интервал попадания случайной переменной. Для симметричного распределения это означает определить интервал . Графически эту задачу можно изобразить так:

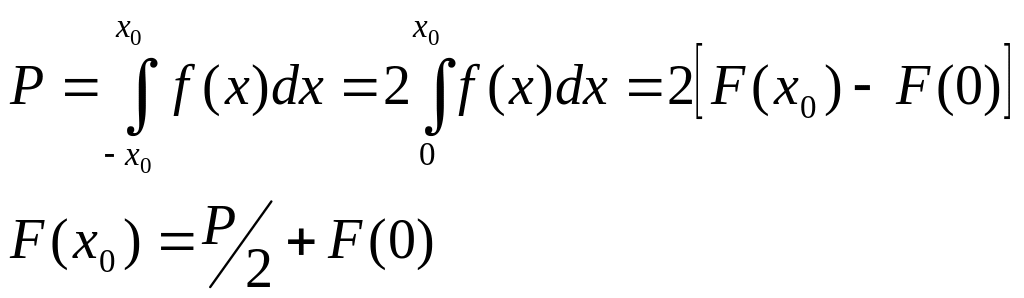
определяется как обратная функция от (плотности распределения). Как правило, это делается по табличным данным.

Законы распределения вероятностей позволяют определить две других важнейших характеристики случайной величины Х: математического ожидания и дисперсии случайной переменной.