Дискретные случайные переменные

Дискретные случайные переменные — это переменные, которые имеют конечное число возможных результатов. Если рассматривать ситуацию с бросанием шестигранной кости, то с каждым из возможных ре­зультатов связана определенная вероятность: для нормальной кости каждая из шести вероятностей равна 1/6. Этот процесс можно смоделировать математически в виде дискретной случайной переменной.

В этом случае мы могли бы назвать случайную переменную Z и определить вероятности для Z, принимающей значения от 1 до 6, и вероятности каждого результата. Вероятности вместе со свя­занными с ними значениями случайной переменной называют рядом распределения (вероятностей), определяющую случайную переменную:

Значения	r=	1	2	3	4	5	6
Вероятности	Z=	1/6	1/6	1/6	1/6	1/6	1/6

Отметим, что независимо от количества возможных результа­тов сумма всех вероятностей должна быть равна единице:

Примерами дискретного распределения являются биномиаль­ное и триномиальное распределения. Подбрасывание монеты приводит к биномиальному распределению результатов, посколь­ку результат может быть либо "орлом", либо "решкой". Цены ак­тивов могут падать, расти или оставаться неизменными, что при­водит к триномиальному распределению, поскольку могут быть три вида результатов — рост, падение и отсутствие изменений.

Рассмотрим пример биноминального распределения.

Пусть производится n независимых испытаний, в каждом из которых событие А наступает с вероятностью р, и не наступает с вероятностью q=1-p. Обозначим через Х случайную величину, равную числу появлений событий А в n испытаниях. Возможные значения величины Х следующие: х₁=0 (событие А не наступило), х₂=1 (событие А наступило 1 раз),…, х_n+1=n (событие А наступило n раз). Вероятности этих возможных значений определяются по формуле Бернулли: .

Возможные значения можно представить в виде таблицы:

Х	х1=0	х2=1	…	х2=m	…	хn+1=n
Р(Х)	qn		…		…	pn

Полученный закон распределения дискретной случайной величины называется законом биноминального распределения.

Непрерывные случайные переменные

Непрерывные случайные переменные — это случайные переменные, которые могут принимать бесконечное количество значений. Например, рентабель­ность активов, кросс-курсы валют, различные биржевые индексы и т.д. Единица измерения может здесь представлять собой бесконечно малую величину.

Для примера рассмотрим доход от какой-либо ценной бумаги. Доходность определяется как отношение: . Количество возможных значений доходности может быть беско­нечно велико. Например, изменение цены актива со 105 единиц до 109 даст доходность, равную 3,8% или 3,81%, или 3,8095% в зависимости от количества знаков после запятой, допускаемого нами при измерении доходности. В этих обстоятельствах нет ни­какого смысла в попытках нахождения вероятности значения доходности равной, скажем, 3,81%. Имеет смысл только нахо­ждение вероятности того, что случайная переменная примет значение на каком-то определенном интервале, скажем, между 3,81% и 3,82%.

Очевидно, что определить вероятность для каждого значения случайной переменной с помощью таблицы, как это делается для дискретных случайных переменных, невозможно. В целях преодо­ления этой проблемы вероятность для непрерывных случайных переменных определяется путем задания так называемой функции плотности вероятно­стей f(Х).

Таким образом, для случайной переменной (X) получаем:

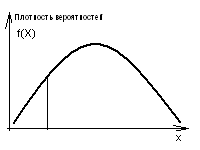
где f — функция плотности вероятностей, которая позволяет задать вероятность каждому значению случайной переменной Х. Функция плотности вероятностей обладает свойством:

(1.1)^*

Иными словами, площадь, целиком заключенная под всей кривой, изображающей плотность распределения вероятностей, равна единице.

Интегральной функцией распределения непрерывной случайной величины Х называется функция F(Х), равная вероятности того, что Х приняла значение меньшее, чем х:

F(X)=P(X<x).

Интегральная функция распределения F(X) и плотность распределения f(X) связаны соотношением , вот почему функцию f(X) еще называют дифференциальной функцией распределения непрерывной случайной величины.

* несобственный интеграл определяется как