Повторные испытания.
Пусть производится несколько испытаний, причем вероятность события А в каждом испытании не зависит от исходов других испытаний, тогда такие испытания называют независимыми относительно А.
Пусть теперь производится n независимых испытаний, в каждом из которых событие А может произойти либо не произойти, причем вероятность появления этого события в каждом испытании равна р и не зависит от исхода других испытаний (независимые испытания). Такая последовательность испытаний называется схемой Бернулли. Так как вероятность наступления события А в одном испытании равна р, то вероятность его ненаступления соответственно равна q=1-p.
В условиях схемы Бернулли вероятность того, что при n испытаниях событие А осуществится ровно m раз, вычисляется по формуле:
Эта формула называется формулой Бернулли.
Пользоваться этой формулой, когда число испытаний достаточно велико (n>15), затруднительно, и в этих случаях используют локальную теорему Лапласа.
Теорема: Пусть р вероятность наступления события А (0<p<1), тогда вероятность того, что в условиях схемы Бернулли событие А при n испытаниях появится ровно m раз выражается приближенной формулой Лапласа:
Где
q=1-p,
,
причем и для этой функции существует
таблица значений.
На вопрос о том: какова вероятность, что в условиях схемы Бернулли событие А, имеющее вероятность появления р, при n испытаниях ( n достаточно велико) появится не менее k раз и не более l раз, отвечает интегральная теорема Лапласа.
Теорема: Пусть р вероятность наступления события А (0<p<1), тогда вероятность того, что в условиях схемы Бернулли событие А при n испытаниях появится от k до l раз, выражается формулой:
,
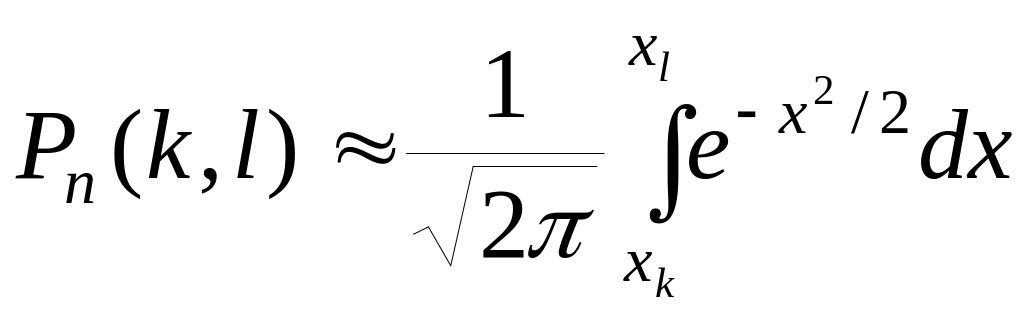где
,
.
Существует
функция Лапласа
,
которая является нечетной
)
и имеет таблицу значений при x>0.
С учетом этого интегральная формула
Лапласа имеет вид:
.
I.2Случайная переменная
Если связать каждое событие из множества событий с каким-либо числом, то мы получим совокупность чисел, появление каждого из которых случайно в результате проведения эксперимента.
Случайная переменная
Х — это функция, принимающая действительные
значения на множестве событий, с помощью
которой мы ставим в однозначное
соответствие каждому событию некоторое
число
или некоторую единственную точку на
действительной оси.
Следовательно, случайная переменная есть некоторое преобразование, которое каждому событию ставит в соответствие единственное алгебраическое значение.
Согласно определению, случайная переменная — это такая переменная, поведение которой неопределенно. Исходя из чего, мы можем только приписать некоторые вероятности возможным значениям таких переменных.
Примеры случайных величин:
1. Число очков, выпавших при однократном бросании игральной кости есть случайная величина, которая может принимать одно из значений: 1, 2, 3, 4, 5, 6.
2. Прирост веса ребенка от одного до двух месяцев жизни – есть случайная величина, принимающая значение от -0,5 кг до 2кг.
3. Число родившихся мальчиков среди 5 новорожденных есть случайная величина, принимающая значение от 0 до 5.
4. Расстояние между эпицентром взрыва бомбы и целью, на которую он была сброшена, — случайная величина, которая может принимать любые положительные значения.
Случайные величины обозначают X, Y, Z, а их возможные значения – x, y, z.
Случайные переменные подразделяются на дискретные и на непрерывные.