MINISTRY OF EDUCATION AND SCIENCE OF UKRAINE
National Aviation University
COMPUTER MODELING
AND SIMULATION
Laboratory Manual for students
Speciality 6.091500 "Computer systems and networks"
Kyiv 2008
Introduction
The given laboratory works are aimed at students fixing the theoretical material studied within the subject “Computer Modeling and Simulation” and acquiring skills for their independent solution of computer modeling and simulation design problems.
The manual contains basic facts about the subject and has been compiled according to the curriculum.
Preparation for the laboratory works requires student’s independent work with appropriate literature. The theoretical material, which is necessary for successful execution of the laboratory works, is considered in the appropriate sections of the subject and given in the works [1-6].
MODULE 1
Laboratory work 1.1
MODELING OF DATA PROCESSING PRECISION IN A DIGITAL SUBSYSTEM
Aim of the work: The work is aimed at studying the precision of data processing in digital subsystems at the instruction-operation level.
Basic Principles
Digital subsystems realize multiplication operations. Algorithms of multiplication and raising to a power are performed with using digital logarithmic (DL) data representation.
The
main statements of DL representation are as follows [1, 2]. Let an
n-capacity
binary number A
be represented in a fixed point format (FP);
where
is the radix.
Each
digit ai
equal to non-zero (
)
may be represented as a position digit number Ni.
Thus the binary number A
can be represented by an array of non-zero digit numbers:
where Ni is the number of non-zero digits ( ).
The conversion from binary representation to the form where each non-zero digit is represented by its number is uniquely determined and realized without additional functional transforms. The substitution operation is performed with each non-zero digit.
The binary numbers A = 1101000101 and B = 101101101 in DL representation have the form: AN = 9.8.6.2.0. and BN = 8.6.5.3.2.0.. For a reverse transfer into binary representation (binary code) a decoding operation should be used.
For
displaying the number of non-zero Ni
digit, ]log2(n
+ 1)[ binary digits are needed (] ∙ [ is the largest nearest
integer), where n
is the operand capacity. In computer memory digit number n
with a number of significant (non-zero) digits Q
occupies the volume of
bits. Note that for the operand representation which has no
significant digits (equal to zero), the descriptor should be used
which designates the equality to zero of this operand. The structure
of DL representation which indicates the number of significant
unities is the most practical. The operand AN
with Q(A)
significant unities is written (for FP format) as signA,Q(A),AN.
Since for writing Ni,
]log2(n
+ 1)[ digits are needed, it occupies the volume of
bits. When DL data representation in the computer is realized, the
simulation of information flows shows that real numbers can be
represented as the array with the number of elements from 5-7 up to
15-20. For example, the operand A
= +1011.0101 is represented as
signA,Q(A),N1N2N3N4N5 → 0,5,3.1.0.-2.-4.
The use of DL representation makes it possible to build a common structure for formats with floating points (FlP) and fixed points (FP). For each number of non-zero digits in FlP format, the representation capacity may be increased by 1 bit; the value of the order is added to each number if this order is the power index of 2. Consequently, the structure of a generalized representation for FlP and FP has the form:
signA |
Q |
N1 + p |
N2 + p |
… |
Ni + p |
… |
Nn + p |
where n is the order.
By means of the common structure for data, the organization of hardware and software can be simplified.
Let
us define the range of number change in computer by using DL
representation. Let Bmax,
Bmin
be the numbers corresponding to maximum and minimum values; n
is the word length. If the coefficient of the range overlapping S
for binary representation is defined as
[3], for DL representation it is similarly defined as
.
The mantissa of the binary operand A
of n
capacity may be used for displaying the position number of
significant unity by DL representation of the number A.
With the capacity n,
the maximum number is defined as 2n
– 1. Taking into account that the number of significant unity is
written with a sign, the maximum
and minimum
numbers are defined by DL representation as:
.
The
range overlapping coefficient
is much greater than the n
capacity. Note that by DL representation, the capacity is increased
from n2
to nDL
=
2(2n
- 1).
Now we give the numbers of binary digits n2 and the digits of DL representation nDL obtained by coding in appropriate n2 and also the ranges of D number change at word lengths nDL.
n2 |
7 |
8 |
9 |
10 |
nDL |
254 |
510 |
1022 |
2046 |
D |
2-127≤x≤2+127 |
2-255≤x≤2+255 |
2-511≤x≤2+511 |
2-1023≤x≤2+1023 |
When the range of data change is extended, the calculation precision becomes higher in hardware. Contrary to the traditional number representation, DL codes permit decrease of the influence of the rounding factor because, along with the most significant digits, the least significant digits can be retained. These latter were usually rejected. This property is of a practical importance: for example, in digital signal processing, the possibility appeared of complex treatment of signals with great and small amplitudes.
The method of number representation determines the performance rules and algorithms for the operations to be made. Consider the realization of computer operations in DL representation.
The rules of digital operation performance (Ni, Nk are the non-zero digits of operands):
addition: Ni + Nk = Ni, Nk, if Ni > Nk;
Ni + Nk = Ni + 1, if Ni = Nk;
subtraction: Ni - Nk = Ni-1, Ni-2, … , Nk, if Ni > Nk;
Ni - Nk = 0, if Ni = Nk;
multiplication: Ni ∙ Nk = Ni, + Nk;
shift of the number at c digits: (N1,N2,…,Nn)-(N1+c,N2+c,…,Nn+c);
AND logic: Ni Λ Nk = 0, if Ni ≠ Nk; Ni Λ Nk = Ni if Ni = Nk;
OR logic: Ni V Nk = Ni if Ni = Nk; Ni V Nk = Ni, Nk, if Ni ≠ Nk.
For organizing data processing in DL representation one should take into account the equality of the position number of a non-zero digit to the logarithm of weight which is defined by this digit. As is shown above, in the rules of multiplication performance, this representation reduces multiplications to the realization of addition-subtraction operations. The product of two numbers in DL representation is realized as the procedure of element-by-element addition of two vectors [1].
Using
DL representation permits extending the range of data processing
(with the given n
capacity) up to
,
which is enough to exclude the influence of the rounding.
Multiplication operations in this laboratory work has been chosen because the exact result of such operations requires doubling the word length, which may not always be realized in multiple calculations.
Example 1: A=2510=110012=4.3.0.DL and B=1310=11012=3.2.0.DL
-
4.+3. 3.+3. 0.+3.
Product A∙B =
4.+2. 3.+2. 0.+2.
= 7.6.4.6.5.3.3.2.0.DL
4.+0. 3.+0. 0.+0.
Next we collect the terms of the resultant array:
A∙B = 8.6.2.0.DL
Transforming it to decimal representation, we have:
A∙B = 28 + 26 + 22 + 20 = 32510.
For modeling the precision of processing, we realize multiplication of the operands A and B in the binary and DL representations. We represent both results in DL codes and compare the numbers of significant units in both variants.
During the multiplication of A = 2510 and B = 1310, a part of partial products is lost for the case of single-precision realization:
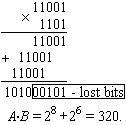
Example 2: A = 29067.12510 = 14.13.12.8.7.3.1.0.-3.DL
B = 897543.510 = 19.18.16.15.13.12.9.2.1.0.-1.DL
We get the product as the array:
33 |
32 |
30 |
29 |
27 |
26 |
23 |
16 |
15 |
14 |
13 |
32 |
31 |
29 |
28 |
26 |
25 |
22 |
15 |
14 |
13 |
12 |
31 |
30 |
28 |
27 |
25 |
24 |
21 |
14 |
13 |
12 |
11 |
27 |
26 |
24 |
23 |
21 |
20 |
17 |
10 |
9 |
8 |
7 |
26 |
25 |
23 |
22 |
20 |
19 |
16 |
9 |
8 |
7 |
6 |
22 |
21 |
19 |
18 |
16 |
15 |
12 |
5 |
4 |
3 |
2 |
20 |
19 |
17 |
16 |
14 |
13 |
10 |
3 |
2 |
1 |
0 |
19 |
18 |
16 |
15 |
13 |
12 |
9 |
2 |
1 |
0 |
-1 |
16 |
15 |
13 |
12 |
10 |
9 |
6 |
-1 |
-2 |
-3 |
-4 |
The ordered array of the product:
33 |
32 |
32 |
31 |
31 |
30 |
30 |
29 |
29 |
28 |
28 |
27 |
27 |
27 |
26 |
26 |
26 |
26 |
25 |
25 |
25 |
24 |
24 |
23 |
23 |
23 |
22 |
22 |
22 |
21 |
21 |
21 |
20 |
20 |
20 |
19 |
19 |
19 |
19 |
18 |
18 |
17 |
17 |
16 |
16 |
16 |
16 |
16 |
16 |
15 |
15 |
15 |
15 |
15 |
14 |
14 |
14 |
14 |
13 |
13 |
13 |
13 |
13 |
13 |
12 |
12 |
12 |
12 |
12 |
11 |
10 |
10 |
10 |
9 |
9 |
9 |
9 |
8 |
8 |
7 |
7 |
6 |
6 |
5 |
4 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
0 |
0 |
-1 |
-1 |
-2 |
-3 |
-4 |
The ordered array of the product with collected terms:
34 33 28 25 24 18 17 15 13 11 10 9 8 7 6 4 1 0 -2 -3 -4.
The product calculated by a PC algorithm is 34 33 28 25 24 18 17 15 14.
The bits of difference between the two products are:
13 11 10 9 8 7 6 4 1 0 -2 -3 -4.
The difference between the two products is 12.5.3.2.-1.-4.DL = 4140.562510. In calculating products of large numbers, the error increases.