4.2 Методические указания по организации самостоятельной работы студентов

Лабораторная работа состоит из трех частей. Первая часть предполагает изучение реального технологического процесса ( объекта ), экспериментальные данные которого используются для подтверждения теоретических положений по созданию автоматизированных систем обработки информации.

Вторая часть посвящена изучению теоретических положений, на которых основан линейный РА, а также методов и способов интерпретации его результатов.

Третья часть включает ознакомление с назначением, структурой, составом и возможностями ПСП STATGRAPHICS, используемого для обработки и отображения статистических данных.

При подготовке к лабораторной работе следует повторить получение статистических характеристик случайной величины, методы построения гистограмм, методы построения корреляционных и автокорреляционных функций и метод одномерного регрессионного анализа по лекционному конспекту, методическим указаниям и литературе [5, стр. 24-52], а также самостоятельно изучить описание технологического объекта (процесса) по методическим указаниям и краткое описание ПСП STATGRAPHICS, которые выдаются преподавателем для каждой группы студентов

4.3 Описание объекта и краткие сведения из теории

В лабораторной работе объектом исследования является технологический процесс, который описывается статической зависимостью Y=F(X), где Х - вектор входа и Y-вектор выхода. Такая зависимость Y от Х может иметь вид

где F⁰ - оператор модели, характеризующий связь между входом и выходом объекта.

При исследовании процесса наблюдателю доступны значения входных X = { x_j } и выходной Y = { y } переменных, которые записываются виде таблицы исходных данных.

Таблица 4.1 - Исходные данные, полученные в результате регистрационного эксперимента

Момент времени	Входные факторы						Выходной фактор
	x1	x2	...	xi	...	xp	y
t1	x11	x12	...	x1j	...	x1p	y1
t2	х11	x22	...	x2j	...	x2p	y2
.	.	.	...	.	...	.	.
.	.	.	...	.	...	.	.
.	.	.	...	.	...	.	.
tI	xI1	xI2	...	xIj	...	xIp	yI
.	.	.	...	.	...	.	.
.	.	.	...	.	...	.	.
.	.	.	...	.	...	.	.
n	хn1	xn2	...	xn j	...	xn p	yn

Вследствие ошибок измерения, которые присутствуют в регистрационном эксперименте, и влияния различных неучтенных факторов, Y является случайным процессом с определенными статистическими характеристиками.

Каждое значение y_t в t-é момент времени есть реакция на одновременное воздействие , j = l..p, в тот же момент времени. Если объект обладает инерцией (запаздыванием), т.е. y_t есть реакция на , то табл.1 необходимо преобразовать, сместив , на вниз по отношению к y_t.

Любая модель (1) отражает только некоторые характерные черты объекта и никогда не бывает его точной копией. Следовательно, нет оснований говорить об "истинной" модели в полном смысле слова. Обычно под "истинным" значением понимают условное математическое ожидание Y при заданных значениях X. т.е.

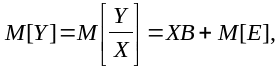(4.2)

где M[.] - символ математического ожидания;

Е - вектор ошибок;

B={b_I}, I=1,m - вектор параметров коэффициентов модели.

Структура выражения (4.2) может быть представлена различными функциями, но в рассматриваемом случае обязательно линейными относительно коэффициентов b_I , I=1,m.

Для создания модели объекта в лабораторной работе используется математический аппарат регрессионного анализа (РА). Как и любой математический аппарат, РА основан на ряде допущений (предположений). Так вектор Е неизвестных значений случайной ошибки должен обладать следующими свойствами:

(4.3)

где M - символ математического ожидания;

n - объем выборки наблюдений;

N(.)- n - мерный нормальный закон распределения;

I_n -единичная матрица;

 ² - дисперсия.

Кроме (4.3), для стандартной нормальной модели регрессии вводится допущение rang(X) = р, т.е. ранг матрицы X, которая предполагается неслучайной, равен числу коэффициентов модели.

При решении задач построения модели реального объекта перечисленные допущения классического РА представляют собой априори заданные требования к свойствам объекта. Однако в действительности объект может не обладать заданными свойствами. В связи с этим при использовании РА для обработки экспериментальной информации необходимо решить ряд статистических проблем:

1) провести статистический анализ экспериментальных данных;

2) задать структуру модели и получить наилучшие точечные и интервальные оценки параметров b_I , I=1,m ;

3) провести интерпретацию модели, проверив гипотезы относительно ее параметров, оценив адекватность модели и проверив предположения, на которых основан РА, используя анализ остатков.

Рассмотрим подробнее сущность перечисленных выше статистических проблем.

Статистический анализ экспериментальных данных проводится с целью определения класса объекта, выбора структуры и метода оценивания параметров регрессионной зависимости. Результаты анализа являются апостериорной информацией для формализованного выбора метода идентификации.

Статистический анализ экспериментальных данных с использованием ПСП "STATGRAPHICS" включает в себя построение двумерных диаграмм рассеивания, вычисление одномерных статистик, построение гистограмм, графиков функций распределения, построение доверительных интервалов для математического ожидания и дисперсии, вычисление корреляционных функций. Проверка гипотез стационарности и случайности выборки данных, к сожалению, не включена в ПСП STATGRAPHICS, поэтому алгоритмы проверки этих гипотез, столь важных при проведении статистического анализа, студенты смогут найти в [7, стр. 148].

В данной лабораторной работе студенты должны изучить методы построения и интерпретации простой регрессионной модели, состоящей из одной зависимой и одной независимой переменной. Пакет STATGRAPHICS дает возможность рассчитать коэффициенты линейной модели у=exp(a+bx), степенной y=ax^b, экспоненциальной у=ехр(a+bx), обратной . Вид модели выбирается студентом, исходя из вида диаграммы рассеивания. Нелинейные модели приводятся к линейным путем логарифмического преобразования или заменой переменной.

Входные и выходные переменные модели задаются преподавателем для каждого студента отдельно.

Лабораторная работа проводится на IBM PC с использованием программы STATGRAPHICS и операционной системы MS DOS.

4.4 Интерпретация результатов

4.4.1.Статистический анализ данных

Двумерные диаграммы рассеивания ( процедура Е1 в блоке Е "Plotting Functions" ) изображают пары значений ( x₁ , y₁ ), (x₂ , y₂),......,( x_n , y_n) и предназначены для оценки вида зависимости между Х и Y ( линейная, нелинейная ), а также визуального определения выбросов и грубых ошибок. Формализованные методы оценки линейности и нелинейности изложены в [ 8, стр. 39]. Алгоритмы оценки выбросов и грубых ошибок представлены в [5, стр. 177]. Исследователь визуально оценивает по двумерным диаграммам рассеивания вид зависимости, наличие выбросов и в дальнейшем оценивает их по формализованным процедурам.

Вычисление одномерных статистик необходимо для оценки мер положения (Average - среднее. Median - медиана. Mode - мода. Geometric mean - геометрическое среднее), мер рассеивания (Variance - дисперсия. Standard deviation - стандартное отклонение, Standard error - стандартная ошибка, Minimum, Maximum, Range - размах, Lower quartile -нижний квартиль. Upper quartile - верхний квартиль, Interquartile range - межквартильный диапазон), формообразующие статистики ( Skewness - асимметрия, характеризующая скошенность распределения, если асимметрия больше 0, то кривая распределения скошена вправо от 0, если меньше 0 - влево; Kurtosis - эксцесс, характеризующий островершинность распределения по сравнению с нормальным распределением N( 0,l ), если эксцесс меньше 0, то кривая имеет более плоскую вершину по сравнению с кривой N ( 0,1 ). Standartized skewness и Standartized kurtosis - соответственно стандартизованные асимметрия и эксцесс (деленные на стандартное отклонение), которые характеризуют близость распределения к нормальному. Если эти коэффициенты находятся в диапазоне [-2,2], то можно ожидать, что распределение близко к нормальному. Если плотность распределения симметрична, то коэффициент асимметрии равен нулю. Для нормального распределения коэффициент эксцесса равен 0. Если распределение сконцентрировано вокруг среднего больше, чем нормальное, то он меньше нуля.

Одномерные статистики позволяют исследователю получить информацию о статистических характеристиках исследуемого процесса и формализовано выбрать метод построения зависимости у = F ( х ).

Построение гистограмм (процедура Frequency Histogram) позволяет строить для заданной переменной гистограмму частот со столбиками одинаковой ширины и высотой, пропорциональной числу значений данных, попадающих в соответствующие интервалы. Гистограммы применяются для построения эмпирического распределения, оценки моментов. Расчет ширины и количества интервалов для построения гистограмм приведены в [7, стр. 145].

Процедура One-Sample Analysis позволяет определить для одной случайной выборки среднее, дисперсию, доверительные интервалы для среднего, дисперсии и проверить гипотезу о равенстве среднего заданной величины.

Проверка гипотезы проводится с помощью критерия согласия [7, стр. 145] при заданном уровне значимости , который равен вероятности отклонения верной гипотезы. Обычно задаются уровнем значимости 0.05. Границы критичной области определяются из статистических таблиц в зависимости от принятого уровня значимости и степеней свободы принятого критерия согласия.

После ввода в поле панели Data vector исследуемой выборки и нажатия клавиши F6 на экране дисплея появляется панель результатов. После величин числа наблюдений, среднего значения, дисперсии, стандартного отклонения и медианы указываются 95%-ный доверительный интервал дня среднего значения при (п-1) степени свободы и 0%-ный доверительный интервал для дисперсии (в последнем случае нижняя и верхняя границы Д отсутствуют). В нижней части панели указаны значения по умолчанию для нулевой гипотезы H₀ : Меаn(среднее значение)=0 при типе альтернативной гипотезы Alt : NЕ(не равно) и при уровне альфа=0.05. 3десь же приводятся результаты проверки нулевой гипотезы: вычисленная t-статистика, уровень значимости и принятое решение: reject или not reject H₀ (отвергается или нет гипотеза H₀ ).

Так как изменение входных и выходных переменных процесса во времени представляют собой случайный процесс, то важную информацию можно получить, анализируя их автокорреляционные и взаимнокорреляционные функции. Прежде, чем строить такие функции, из данных необходимо исключить временной тренд. Автокорреляционная функция случайного процесса (АКФ) показывает зависимость значений процесса через различные промежутки времени. АКФ в общем случае зависит от начального момента времени и интервала сдвига. При этом значение функции в нулевой момент времени равно 1. Ненормированная автокорреляционная функция называется автоковариационной и ее значение в нулевой момент равно дисперсии. Вычисление АКФ осуществляется с помощью функции Autocorrelation Analysis раздела 0 Time Analysis (анализ временных рядов).

Автокорреляционная функция случайного процесса в общем случае вычисляется по формуле (4.4) для процессов, статистические характеристики которых не зависят от начала отсчета.

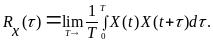(4.4)

Основным приложением автокорреляционной функции процесса является исследование того, в какой степени значения процесса в некоторый момент времени влияют на его значение в будущий момент времени t. В случае гармонического колебания автокорреляционная функция повторяет свою форму во времени в противоположность автокорреляционной функции случайного процесса, которая стремится к 0 при больших значениях сдвига (если m_x = 0 ).Поэтому очевидно, что АКФ представляет мощное средство для выявления детерминированных процессов, которые могут маскироваться случайным фоновым шумом. Корреляционные функции находят широкое применение в стохастической теории идентификации и управления. Они являются математическим описанием случайного процесса.

4.4.2 Интерпретация простой регрессии

Интерпретация результатов расчета сводится к построению интервальных оценок регрессионной модели, проверке основных гипотез и оценке адекватности.

После заполнения полей и нажатия клавиши F6 на экране появляются результаты в виде двух таблиц. В первой таблице приводятся результаты регрессионного анализа. Модель регрессии представлена в виде

где а- свободный член и соответствует оценке ( Estimate ) параметра ( Parameter ) intercept. Оценка Ь соответствует параметру slope таблицы регрессионного анализа. Далее выводятся стандартные ошибки ( standart errors ) коэффициентов регрессии: для а и для b. В следующем столбце таблицы выводятся значения t -распределений для коэффициентов модели ( Т- value ). В последнем столбце выводятся вероятностные значения коэффициента доверия (Prob. Level ) - уровень значимости для гипотезы H₀..

Если эта величина меньше 0.05, то гипотеза H₀ отвергается и параметр считается значимым.

Стандартная ошибка коэффициентов модели используется для проверки гипотез и построения доверительных интервалов коэффициентов регрессии. В этом случае ошибки Е уравнения У = ХА.+Е должны быть распределены по нормальному закону ( E  N ). На практике принимают, что E ~ N, ò.ê. Е отражает совокупное действие множества не учитываемых факторов. Тогда, согласно центральной предельной теореме теории вероятностей, ошибку Е можно рассматривать как случайную величину с нормальным законом распределения. Такое предположение используется для построения интервальных оценок. Интервальной оценкой параметра A₀ будет интервал I=A₂₀ - A₁₀ на оси A, который с заранее выбранной вероятностью P=1- покрывают истинное значение параметра:

Построить интервальную оценку для параметра A₀ - значит определить по данным выборки (или по точечной оценке А) конечные значения A₀, всегда отличающиеся от своей выборочной оценки А, будет заключено в интервале { A₂₀, A₁₀ }.

В ПСП STATGRAPHICS выведены значения стандартной ошибки коэффициентов регрессии, которые вычисляются по формулам:

где

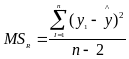
Доверительный интервал для свободного члена уравнения регрессии вычисляется по формулам

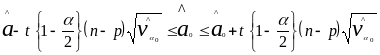(4.5)

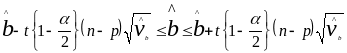(4.6)

где  -уровень значимости.

Вероятность того, что гипотеза Н0 будет отвергнута в случае, когда она на самом деле верна, равна заданной вероятности , которую называют уровнем значимости.

В ПСП STATGRAPHICS доверительные интервалы для коэффициентов не рассчитываются. Выдаются только значения среднеквадратичных ошибок коэффициентов модели, т.е. значения и .

Для определения границ изменения а и b по формулам (4.5) и (4.6) необходимо отыскать табличные значения t-распределения для заданного значения уровня значимости  и степеней свободы (n-р). Значимость коэффициентов регрессии оценим по проверке гипотезы H₀^’’: b_j=b_j^*, против альтернативной гипотезы H₀^’’: b_j=b_j^*. Для этой цели используется статистика

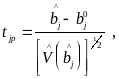
где - оценочное значение коэффициентов регрессии;

истинное значение коэффициентов регрессии.

Величина t_j имеет t-распределение с (n-р) степенями свободы лишь при соблюдении условий ноль - гипотезы H₀^’’. Задавшись уровнем значимости  и определив табличное значение , можно провести сопоставление табличной и расчетной величин:

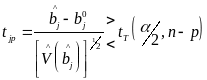(4.7)

Если , то гипотеза H₀ принимается, в противном случае она отвергается в пользу альтернативы H₁^’’: b_j  b_j^* .

В ПСП STATGRAPHICS такая процедура не выполняется, но приводятся расчетные значения коэффициентов t_jp . Исследователю достаточно легко оценить значимость b_j по формуле (4.7). Для этого необходимо задаться уровнем значимости  и значением , находимым по таблицам t-распределения Стьюдента.

Значимость коэффициентов регрессионной модели в ПСП отражает величина Prob. level, которая является площадью под функцией плотности распределения N ( 0,1 ). Если P а, то гипотеза H₀ не отвергается.

Рассмотрим интерпретацию дисперсионной таблицы регрессионного анализа. В таблице приводятся следующие данные:

SS_d - сумма квадратов отклонения, обусловленная регрессией;

SS_d = . Первый столбец таблицы, строка - модель;

SS_R - сумма квадратов, обусловленная ошибками;

SS_R= .

Во втором столбце печатаются степени свободы для SS_d и SS_R (V_d ,V_r)

В третьем столбце печатаются средние квадраты отклонений SS_d и SS_R , вычисленные по формулам

где V_d и V_r - степени свободы соответственно V_d = 1; V_r = п - р.

В четвертом столбце печатается F-отношение

(4.8)

Используя (4.8) можно проверить гипотезу о том, что простая линейная регрессия Y по Х отсутствует, т.е. гипотезу H₁^’’: b_j =0 против альтернативной гипотезы H₁^’’: b_j  0 .

Если верна гипотеза H₀ , то F₀ имеет F - распределение с V_d=1 и V_r=n-p степенями свободы. P - значения есть площадь под кривой плотности распределения справа от F_0. Если P меньше, чем уровень значимости , то H₀ отвергается.

В ПСП STATGRAPHICS приводится расчетное значение F_0P. Его можно использовать при оценке адекватности модели. Для этой цели необходимо задаться уровнем значимости  и выбрать по таблицам F-распределення табличное значение F_T по заданным  и (n - p) степеням свободы. Если F_p>F_T, то можно утверждать, что модель адекватно описывает экспериментальные данные. Ниже таблицы печатается коэффициент корреляции, стандартная ошибка оценки и величина коэффициента детерминации, равного для линейной модели квадрату коэффициента корреляции, объясняющего долю зависимости у от х в процентах. После нажатия клавиши ENTER, получают на экране окно с меню, содержащее следующие опции:

Plot fitted line - график исходных точек и линии регрессии;

Plot residuals - график остатков для подобранной модели;

и т.д.

4.5 Порядок выполнения работы

1.Запустить на выполнение пакет программ статистической обработки STATGRAPHICS.

2.Ввести заданный преподавателем набор экспериментальных данных, используя раздел A "Data Management" ( управление данными ) главного меню пакеты

3. Провести статистический анализ данных, в который входит решение следующих задач:

- построение двумерных диаграмм рассеивания с использованием программы "X-Y Line and Scatterplots"( двумерные диаграммы рассеивания ) раздела Е "Plotting Function" ( графики функций ) главного меню:

- вычисление одномерных статистик с использованием программы "Summary Statistics" ( одномерные статистики ) раздела F "Descriptive Methods" ( описательные методы ) главного меню,

- построение гистограмм с использованием программы "FREQUENCY HISTOGRAM" ( гистограмма частот ) раздела F, -вычисление одновыборочного Т-критерия (Стьюдента) и доверительных интервалов для математического ожидания и дисперсии с использованием программы "Опе-Sample Analysis" (одновыборочный анализ) раздела G 'Estimation and Testing" (оценивание и проверка гипотез),

- вычисление автокорреляционных функций с использованием программы "Autocorrelation Function" раздела О "Time Series Analysis" ( анализ временных рядов);

- по указанию преподавателя проверить гипотезу стационарности и случайности набора экспериментальных данных.

4. Построить простую регрессию, используя программу "Simple Regression" (простая регрессия) раздела К "Regression Analysis" ( регрессионный анализ ) и вывести результаты расчетов.

5. Провести интерпретацию результатов и сделать выводы, решая следующие задачи:

- оценить значимость коэффициентов модели, полученной с использованием простой линейной регрессии, по критерию Стьюдента; - оценить адекватность модели по F-êðиòåðиþ.

4.6 Содержание отчета

Каждый член бригады оформляет отчет, в котором приводит:

- цель и задачи лабораторной работы;

- последовательность статистического анализа данных;

- назначение и краткую характеристику используемых программ;

- распечатку результатов расчетов с комментариями-,

- интерпретацию полученных результатов;

- выводы по проделанной работе.

4.7 Контрольные вопросы

1. Объяснить сущность регрессионного анализа.

2. Где используются результаты расчета одномерных статистик?

3. Каковы вычислительные процедуры регрессионного анализа?

4. Каковы предпосылки классического регрессионного анализа?

5. Каковы основные принципы интерпретации результатов?

6. Какие критерии используются для оценки результатов регрессионного анализа?

7. Какие программы пакета STATGRAPHICS использовались при выполнении работы? В каком виде представлены результаты работы программ?

ЛАБОРАТОРНАЯ РАБОТА №5

Сравнительная оценка методов обработки данных

5.1.Цель работы

Изучить методы построения многомерных линейных статических моделей технологических процессов, провести интерпретацию полученных результатов и принять решение о целесообразности использования модели для управления. Получить навыки применения многомерной регрессии, пошагового метода и гребневой регрессии для построения статических моделей.

5.2.Методические указания по организации самостоятельной работы студентов

Лабораторная работа состоит из трех частей.

Первая часть посвящена изучению предположений и предпосылок использования многомерного регрессионного анализа и интерпретации результатов построения моделей.

Вторая часть предполагает изучить процедуру пошагового метода и оценить информативность независимых переменных.

Третья часть посвящена изучению гребневого метода построения моделей.

При подготовке к лабораторной работе следует повторить методы

множественной регрессии, пошагового и гребневого методов. Изучить

краткое описание ПСП STATGRAPHICS.

5.3. Краткие сведения из теории

5.3.1. Множественная линейная регрессия (МЛР).

Проблема МЛР позволяет определить связь между одной зависимой

переменной и одной или несколькими независимыми переменными.

Рассмотрим проблему предсказания одной переменной Y с помощью

Р переменных X₁ ,X₂ ,...,X_p , p>1.

Пусть B=(b0,...,bp)^T - вектор параметров модели размерности

((k+1)*1),Y=(y_p ,...,y_n )^T - вектор из n наблюдений, е=(е₁ ,...,e_n ) -

вектор из n ошибок, X^T - матрица плана размерности n*(p+1),

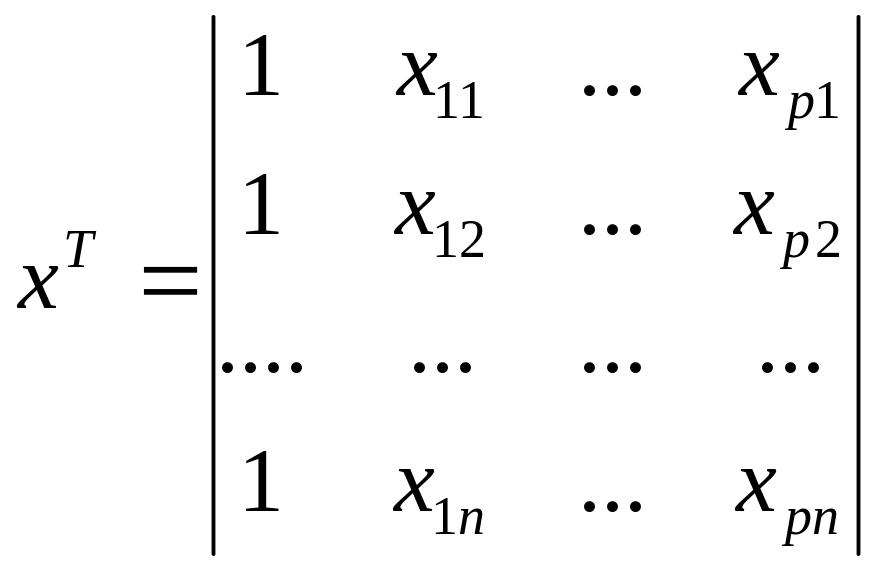
Уравнение регрессии записывается в виде

Y=XB+e (5.1)

где е следует нормальному закону распределения N(0, ² I).

Сумма квадратов отклонения для данной модели:

S² =(Y-X^TB)^T (Y-X^TB).

Оценки параметров уравнения (5.1) определяются по методу

наименьших квадратов /1/из решения системы нормальных уравнений:

(XX^T)B=XY,

откуда

B=(XX^T)^-1 XY.

Ковариационная матрица оценок равна

COV(b)=² (XX^T)^-1 .

Несмещенная оценка дисперсии

MSR=S² =(n-p-1)^-1 (Y-X^T B)^T (Y-X^T B).

Представим центрированную форму модели множественной регрессии

в виде

где .

МНК-оценками для будут, как и раньше, .

Оценкой для будет .

Преимущество этой модели заключается в том, что оценки

не коррелированны с .Это упрощает нахождение

доверительных интервалов для предсказанного значения .В матричных

обозначениях центрированная модель для оценок по МНК имеет вид

b=(b ,...,b ) =A g,

где А - матрица сумм квадратов и смешанных произведений отклонений

с элементами

g есть (k*1) вектор с k-м элементом

Ковариационная матрица оценок

.

Для каждого стандартная ошибка коэффициента ecть

оценка стандартного отклонения оценки от , . Каждая

из этих величин является функцией от MSR и имеет степеней

свободы. В этом случае %-ный доверительный интервал для

есть

Для линейной модели вида количество оцениваемых

коэффициентов m равно количеству входных переменных .

По таблице дисперсионного анализа проверяется гипотеза Н₀ :

, которую можно рассматривать как гипотезу о том, что

не улучшают предсказание Y относительно

. Альтернативная гипотеза состоит в том, что не все коэффициенты

равны нулю, то есть некоторые из х улучшают предсказание Y по

~ -

сравнению с . Статистикой критерия является F-отношение

. (5.2)

Соответствующее Р-значение есть площадь области F под кривой

распределения справа от точки, соответствующей вычисленному

значению F. Адекватность модели проверяется по выражению (5.2).

Если рассчитанное значение F по (5.2) окажется больше

критического F_КР = F_ТАБЛ, взятого из таблиц для данного числа

степеней свободы и принятого уровня значимости , то это будет

означать, что остаточная дисперсия MSR статистически меньше

дисперсии MSD относительно . В этом случае полученное уравнение

регрессии можно считать работоспособным.

В таблице дисперсионного анализа множественной линейной

регрессии печатается множественный коэффициент корреляции МКК. МКК

является мерой линейной зависимости между Y и набором

переменных , причем . Нулевое значение МКК

указывает на то, что Y не зависит (линейно) от набора переменных

,а значение 1 указывает на полную линейную зависимость,

при которой переменная Y точно равна линейной комбинации переменных

.Оценка R имеет вид:

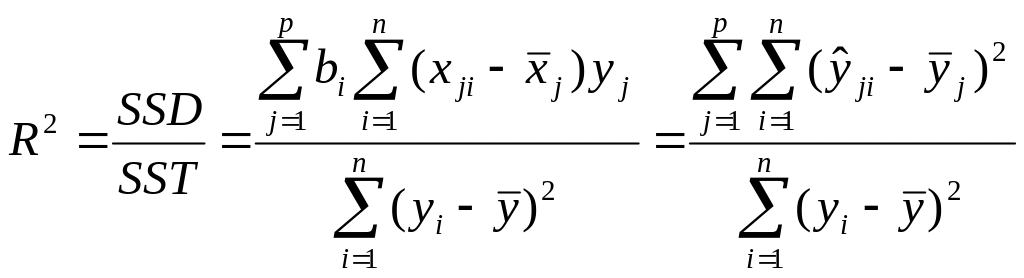
Второе применение оценки R следует из того, что

,

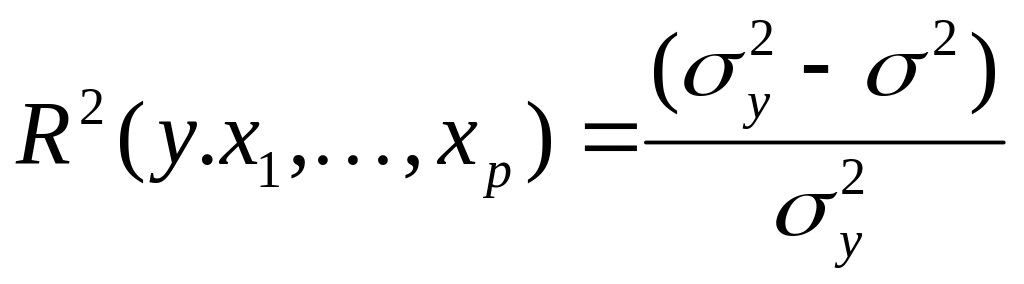где - дисперсия условного распределения, которое определяется

подмножеством значений Y при фиксированных значениях

Квадрат R оценивает "долю дисперсии Y", объясненную линейной

регрессией Y по .

Величина есть доля стандартного

отклонения Y, оставшаяся "необъясненной" зависимостью от .

Для проверки предположений модели простой линейной регрессии

печатаются графики остатков (residuals) в зависимости от

или , i=1,...,n. График в сопоставлении с (i=1,...,n,

j=1,...,p) содержит информацию:

1) о наличии аномальных наблюдений или случаев отклонений по

j-й независимой переменной;

2) об отсутствии линейности по х, что должно служить указанием

для дальнейшего преобразования.

График относительно (i=1,...,n) доставляет информацию о

выполнении предположений случайности и независимости ошибок , а

также предположения об однородности дисперсий .

Критерии оценки случайности, стационарности приведены в [5.

стр.164,169]. критерий сериальной корреляции Дарбина-Ватсона,

который является Проверку гипотезы о независимости ошибок можно

осуществить, используя строгим для случая независимости

от Х [5. стр. 289].

5.3.2. Интерпретация результатов множественной линейной

регрессии.

Модель множественной линейной регрессии получают в виде

.

После заполнения полей и нажатия клавиши F6 появляется таблица

"Model fitting results", где печатаются коэффициенты

модели, стандартные ошибки коэффициентов и расчетные значения

t-критерия t_p. Стандартная ошибка коэффициента есть оценка

стандартного отклонения оценки от , i=1,...,p., t-статистики,

рассчитываемые путем деления коэффициентов на их стандартные ошибки,

и уровни значимости для каждой t-статистики(т.е. вероятности того,

что будет иметь место большая величина t при отсутствии заметного

вклада от соответствующей переменной. В нижней части таблицы

приводятся рассчитанные величины скорректированного коэффициента

детерминации, стандартной ошибки (SE), расчетное значение

статистики Дурбина-Ватсона. Коэффициент детерминации (R-squared)

является мерой адекватности регрессионной модели. Чем больше его

значение, тем выше степень адекватности уравнения регрессии.

Расчетное значение статистики Дурбина-Ватсона используется для

проверки гипотезы о независимости остатков.

При нажатии клавиши F5 на экране появляется меню опций печати,

а при нажатии клавиши Esc -следующее меню опций:

Analysis of variance - анализ дисперсий для полной регрессии с

расчетом F-статистики и уровня значимости для

проверки адекватности модели

Conditional sums of - условные суммы квадратов, определяющие вклад

squares каждой переменной, вводимой в модель, в полную

сумму квадратов регрессии

Plot residual - график остатков в зависимости от прогнозных

значений, их индексов или любой другой

переменной (по выбору пользователя).

Summarize residual - суммарные статистики остатков.

Plot predicted value -графики прогнозных значений в зависимости от

наблюдаемых значений для зависимой переменной

(с включением линии с наклоном равным 1)

Probability plot - график функции распределения остатков на

вероятностной сетке нормального распределения.

Дисперсионный анализ данной модели представляется таблицей.

Таблица результатов дисперсионного анализа

Источник дисперсии	Сумма квадратов	Степени свободы	Средний квадрат	F-отношение
Регрессия
Отклонение от регрессии
Полная

Стандартная ошибка позволяет построить 100(1- )%-ный

доверительный интервал для b

, i=1,...,p.

После нажатия клавиши Esc и выбора операции Analysis of

variance получают результаты дисперсии для полной регрессии, по

которой можно судить об адекватности модели. Сумма квадратов

отклонений, обусловленная регрессией представлена в первой

колонке (Sum of Squares) в строчке Model и определяется следующим

образом:

Стандартная ошибка представлена вторым числом в строке Error,

обозначается и определяется из выражения:

Вторая колонка определяет степени свободы. Для - это ;

для ;

Третья колонка определяет средний квадрат отклонений (Mean

Square) относительно регрессии и стандартной ошибкой и

определяются соответственно:

; ;

Четвертая колонка определяет расчетное значение F-критерия

(F-Ratio)

;

Полная дисперсия определяется выражением ,

степень свободы .

Задаваясь уровнем значимости и соответствующими степенями

свободы , определяют табличное значение F_ТАБЛ. .Модель можно

считать работоспособной, если F_Р.>F_ТАБЛ. Однако в связи с тем, что

ошибки (остатки) в усеченных выборках, как правило, не подчиняются

нормальному закону распределения, F_Р должно быть в 5-6 раз больше,

чем F_ТАБЛ.[1]

Пятая колонка определяет коэффициент доверия (Level), который

должен быть меньше заданного уровня значимости. В этом случае

гипотеза Н0 отвергается с уровнем значимости , в противном случае

Н0 принимается.

В конце таблицы печатаются значения множественного (R-squared)

коэффициента корреляции и скорректированное его значение (R-

squared(Adj.for d.f), а также значение стандартной ошибки оценки и

величину статистики Дурбина-Ватсона для оценки независимости

остатков.

По таблице "Model fitting results" с помощью t-распределения

проверяется гипотеза H₀ : , где - заданная константа,

относительно односторонней и двусторонней альтернатив. Статистика

критерия в этом случае имеет вид :

,

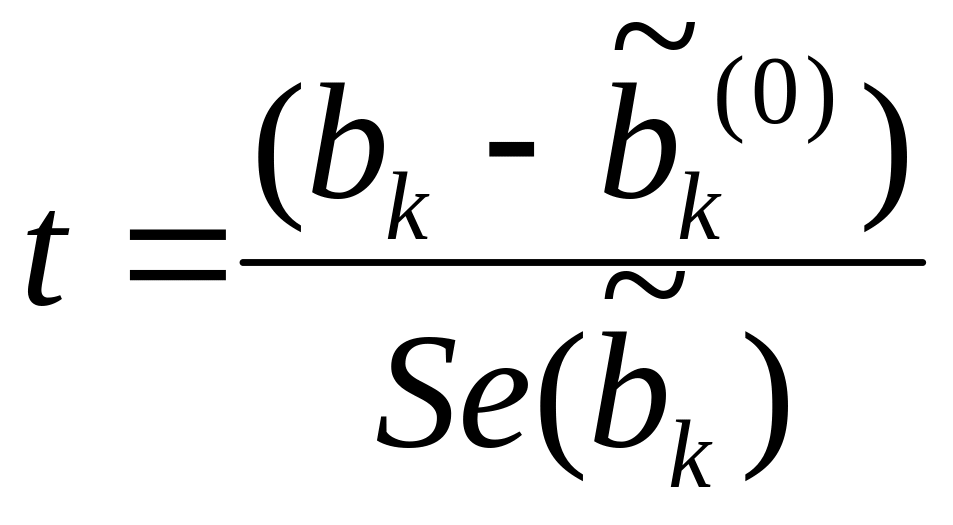а Р-значение получается с помощью кривой плотности распределения

в зависимости от альтернативной гипотезы.

Для оценки вклада каждой переменной, вводимой в модель,

используется опция "Conditional sums of squares" .

В таблице печатаются условные суммы квадратов для каждой

переменной , т.е. приводятся величины

;

Значимость входных переменных оценивается по значению P-Value.

Для проверки предпосылок и предположений регрессионного анализа

необходимо использовать графики остатков в зависимости от любой

численной переменной (Plot residual), график зависимости

наблюдаемых и прогнозируемых значений (Plot predicted), график

вероятностного распределения остатков (Probability Plot),

значение Durbin - Watson static.

Выбрав опцию Plot residual, а затем введя по запросу системы

переменную и имя переменной , можно получить график остатков в

зависимости от любой численной переменной, длине которой равна

длина зависимой переменной, вне зависимости от того, учтена ли она

в принятой модели.

Горизонтальная линия характеризует нулевой уровень

остатка. Такой график полезен для визуального выявления выступов,

нелинейностей или других аномалий остатков.

По графику можно судить о случайном характере остатков

относительно нулевой линии.

Выбрав из меню опций пункт Plot predicted value, можно

получить график зависимости наблюдаемых и прогнозируемых значений.

Этот график полезен для выявления случаев, когда дисперсия не

постоянна или когда необходимо преобразование зависимой

переменной. Если точки располагаются довольно равномерно

относительно диагональной линии, то можно сделать вывод о

приемлемости модели.

С помощью опции Probability Plot строится график

вероятностного распределения остатков. На графике показана прямая

линия, соответствующая наилучшей подобранной функции нормального

распределения. По степени близости точек к этой прямой можно судить

о близости распределения остатков к нормальному и , соответственно,

об адекватности модели.

С помощью опции Component effect plot после выбора по запросу

системы переменной можно получить график компонентного влияния

одной (х) переменной на другую (y).

Такой график полезен для суждения об относительной величине

остатков по отношению к "обьясняющей (x)" переменной. В случае, если

остатки относительно малы по сравнению с изменением величины y,

предсказанными в зависимости от x, можно утверждать, что x

обеспечивает получение полезной информации для прогнозирования y.

Опция Confidence interval позволяет построить доверительные

интервалы для оценок коэффициентов при принятой доверительной

вероятности .

По таблице условных сумм квадратов "Further ANOVA for

variables in the order fitted" проверяется гипотеза Н₀. Приводится

Р-значение, полученное после сравнения F с процентилями

распределения F для соответствующих степеней свободы.

5.3.3. Пошаговая линейная регрессия.

Стандартная пошаговая процедура (F-метод) состоит во

включении и удалении переменных с помощью квадрата t-критерия,

имеющего F-распределение.

Предположим, что в набор С уже включено k переменных,

k=0,1,...,p-1. Тогда значение F для включения переменной х, (не

входящей в С), вычисляется по формуле

. (5.3)

где -частный коэффициент корреляции, квадрат которого

определяет долю остаточной дисперсии Y, "объясненной" добавлением

переменной X к набору С. Величина служит статистикой критерия

для проверки гипотезы о том,что предсказание Y значимо не улучшится

при включении х в набор С, т.е. Н₀ : .Если эта гипотеза верна,

то статистика распределена по закону F(1,n-k-2).

Аналогично, величина F удаления для какой-либо переменной Х из

С служит статистикой критерия для проверки гипотезы о том, что

набор С₁ , получившийся из набора С при удалении Х и содержащий

k₁=k-1 переменных, предсказывает Y так же хорошо, как и набор

С. Иными словами, проверяется гипотеза Н₀ : и статистикой

критерия является величина F удаления

, ( 5.4)

распределенная по закону , если Н₀ верно. Правило

останова основано на задании допустимого минимума F-включения и

допустимого минимума F-удаления, .

Рассмотрим шаги стандартной процедуры.

Шаг 0. Вычисляются простые коэффициенты корреляции и

величина F-включения , .

Статистика критерия дается выражением

которое получается из формулы ( 5.3) подстановкой k=0 или как квадрат

t-статистики.

Шаг 1. Переменная , которой отвечает наибольшее значение

F-включения (или, что эквивалентно, наибольшая величина квадрата

коэффициента корреляции с Y), выбирается как наилучший предиктор

для Y. Вычисляются коэффициенты регрессионной модели по методу

наименьших квадратов, строится таблица дисперсионного анализа и

определяется множественный коэффициент корреляции .

Величина F-удаления для в этом случае совпадает с

величиной F-включения. Далее вычисляются коэффициенты частной

корреляции и значения F-включения

для , , т.е. для каждой переменной, не вошедшей в

уравнение регрессии. Эта статистика имеет 1 и n-3 степеней свободы

и служит для проверки гипотезы Н₀ : , , .

Если все вычисленные значения F-включения меньше

установленного минимума, то далее выполняется шаг S. В противном

случае происходит переход на шаг 2.

Шаг 2.Переменная , имеющая наибольшее значение F-включения

(или, что эквивалентно, наибольший квадрат частного коэффициента

корреляции с Y при фиксированном значении ), выбирается как

наилучший предикатор для Y при условии, что уже выбрана переменная

.Вычисляются МНК-оценки коэффициентов, строится таблица

дисперсионного анализа, вычисляется множественный коэффициент

корреляции и значения F-удаления и .

Эти статистики имеют 1 и n-3 степеней свободы и определяются

выражениям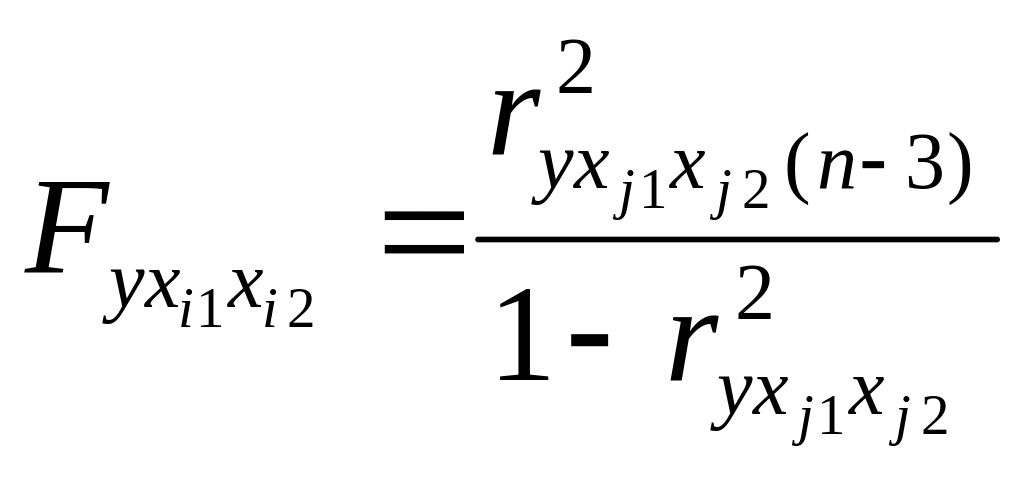и:

и .

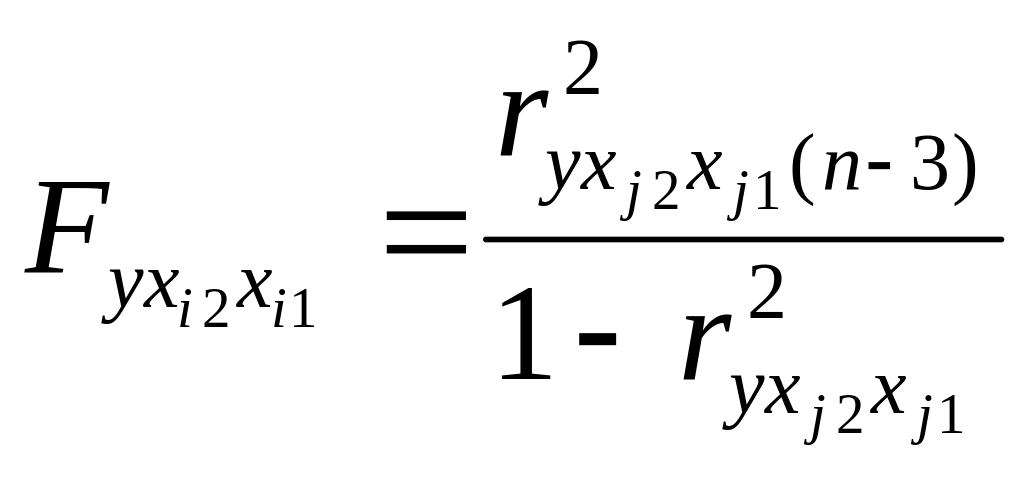Они используются для проверки гипотезы Н0: .

Вычисляются частный коэффициент корреляции

и значения F-включения

для проверки гипотезы Н₀ ; c 1 и n-4 степенями свободы

при , , .

Если все значения F-включения меньше установленного минимума,

то далее выполняется шаг S. В противном случае происходит переход

на шаг 3.

Шаг 3. Пусть L обозначает набор из l независимых переменных,

которые включены в уравнение регрессии. Производятся следующие

действия:

1) если какое-либо из значений F-удаления для переменных из L

меньше, чем соответствующий минимум, то переменная, которой

соответствует наименьшее значение F-удаления, удаляется из набора и

выполняется пункт 2 шага 3 с заменой l на l-1. Если для всех

переменных, не входящих в L, значение F-включения меньше

установленного минимума, то выполняется шаг S. В противном случае

в набор L добавляется переменная, которой соответствует

максимальное значение F-включения, и l заменяется на l+1;

2) определяются коэффициенты модели по МНК, строится таблица

дисперсионного анализа, вычисляются множественный коэффициент

корреляции между Y и переменными из L и значения F-удаления

для Y и переменной из L при заданных остальных l-1

переменных из L. Каждая из этих величин имеется 1 и n-l-1 степеней

свободы и используется для проверки гипотезы Н; .

Определяется величина частного коэффициента корреляции и

значения F-включения между Y и каждой переменной , не

входящей в L, при данных переменных из L. Эта статистика имеет 1 и

n-l-2 степеней свободы и проверяет гипотезу Н₀; для ,

не входящих в L, .

Шаги 4,5,.... Рекуррентно повторяется шаг 3. Шаг S

выполняется, если:

1) значения F-включения для всех переменных, не входящих в L,

меньше установленного минимума;

2) для всех переменных из L значения F-удаления больше

установленного минимума;

3) число включенных переменных равно р.

Шаг S. По запросу пользователя печатается таблица результатов

для каждого шага, в которой выводится номер шага, номер включенных

и удаленных переменных, значения F-включения и F-удаления и

множественного коэффициента корреляции между Y и включенными

переменными.

5.3.4. Интерпретация результатов

пошаговой линейной регрессии

Рассмотрим принцип останова процедуры включения и исключения в

пошаговой процедуре.

Наилучшее значение набора предикаторов "Н" может быть

определено, когда все вычисляемые значения F-включения станет

меньше заданных значений F-включения и F-удаления.

Рассматривают несколько правил останова при реализации

пошаговых процедур. [1]Стандартное правило останова, которое

основано на расчете F-включения и F-исключения и сравнение их с

допустимыми значениями.

Правило остановки, основанное на изменении , предполагает

проверку гипотезы H₀: с помощью статистики t

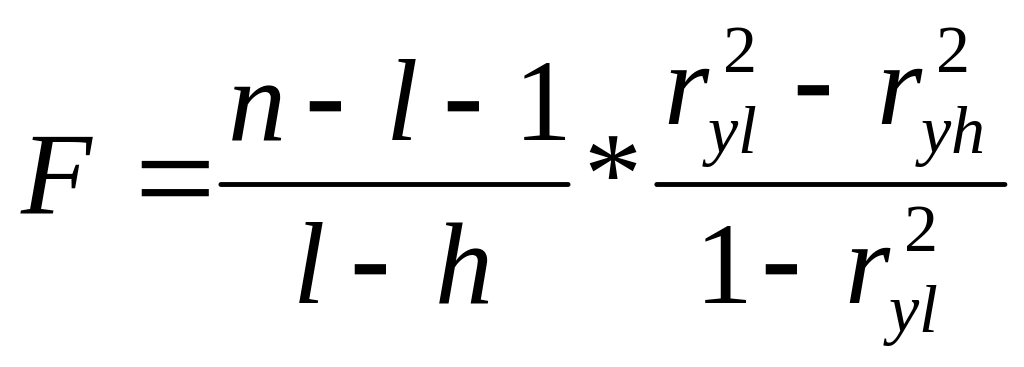
где l- набор входных переменных, входящих в модель,

h- набор переменных, входящих в уравнение на промежуточном

шаге.

Если гипотеза верна, то величина F имеет F- распределение с

l-h и n-l-1 степенями свободы. Этот критерий применяется

последовательно на каждом шаге до тех пор, пока не будет получено

первое незначимое значение F.

Третье правило останова основано на проверке гипотезы о том,

что при переходе к следующему шагу безусловный средний квадрат

ошибки (UMSE) не убывает.

В ПСП STATGRAPHICS используется стандартное правило, важно

выбрать значение F-включения и F-исключения.

В ПСП STATGRAPHICS по умолчанию предполагается, что минимум

F-включения равен 4.0. Для удаляемых переменных также выбирается

допустимый принцип F-удаления ( это величина должна быть меньше

минимума F-включения).

Значение минимума F-включения эквивалентно максимуму уровня

значимости, т.е. min F-включения = F_1-(1,) для некоторого числа

степеней свободы . Обычно, , а рекомендуемое значение

составляет 0.15, хотя можно установить . В работе [1]

показано, что если предположительней использовать стандартное

правило останова с (т.е. min F-включения приблизительно

равно 2.5).

На панели ввода данных первые 6 полей аналогичны процедуре

множественной регрессии и имеются следующие дополнительные поля:

Method : Forward - прямой метод;

Backward- обратный;

None - стандартная регрессия;

F-enter : F-статистика, при превышении которой переменная

вводится в модель (по умолчанию 4);

F-remove : F-статистика, ниже которой переменные будут удаляться

из модели по умолчанию -4; F-remove не должна превышать

F-enter);

Max.Steps: максимальное число шагов, выполняемых системой перед

остановкой процесса отбора (по умолчанию - 500);

Control : автоматическое (Automatic) или ручное (Manual)

управление исключением переменных (по умолчанию -

ручное).

После заполнения полей и нажатия клавиши F6 система начинает

подбирать модель на основе установленных критериев. При ручном

управлении пользователь должен нажимать клавишу ENTER для

завершения каждого шага до получения итоговой модели. Затем

пользователь может нажать клавишу F5, после чего появляется

временное окно с опциями, позволяющими ему корректировать модель:

Forse var.into model - включить переменную в модель;

Remove var.from model- исключить переменную из модели.

Переменная задается номером из списка переменных на экране.

На нулевом шаге все независимые переменные, введенные

пользователем, показываются в правой части панели в столбце

Variables Not in Model (переменные не в модели) и для каждой

переменной приводятся рассчитанные величины частных коэффициентов

корреляции P.corr и F-статистики (F-enter), которые будет иметь

каждая переменная при ее вводе в модель на следующем шаге. При

нажатии клавиши ENTER система вводит в модель переменную, для

которой величина F-статистики максимальна. Введенная переменная

появляется в левой части панели в столбце Variables in Model и для

всех переменных пересчитываются все статистики. Аналогичным образом

продолжается процесс подбора модели до получения сообщения о выборе

итоговой модели: Final Model selected. Те переменные, для которых

F-статистика меньше установленной пороговой величины F-enter, в

модель не вводятся и остаются в правой части панели.

5.3.5. Гребневой анализ (Ridge Regression)

Гребневой анализ используется при мультиколлинеарности.

Мультиколлинеарность приводит к тому, что матрица X’X оказывается

плохо обусловленной, поэтому оценки метода МНК A=(X’X)^-1 X’Y будут

неустойчивы.

Путем добавления малого положительного числа к

диагональным элементам матрицы X'X ее регуляризируют, что приводит

к тому, что новые оценки являются более устойчивыми. Проблема

мультиколлинеарности - не вычислительная, а статистическая и

заключаеся в улучшении статистических оценок.

Центральная проблема гребневых оценок - выбор параметра

гребневых оценок. Гребневые оценки образуют целый класс оценок.

Поэтому для каждой конкретной регрессии приходится перебирать

несколько значений параметров регуляризации, делать расчеты с

разными матрицами регуляризации и т.п., т.е. провести целое

исследование. На место одной оценки, одной модели регрессии как в

МНК приходится целое семейство моделей и оценок.

В разделе K выбирается опция "Ridge Regression", вводятся

зависимые (Y) и независимые переменные (X) и строится "ридж-след"

для каждой координаты aj(k), где k выбирается на основе визуального

анализа. Значение aj целесообразно выбирать для установившихся

значений.

5.3.6. Нелинейные модели (Nonlinear Regression)

Задача нелинейного оценивания, выраженная в форме условий

n 2

минимума функции , где - соответствующие

веса, возможно равные единице, является задачей оптимизации в

пространстве параметров, когда величины и считаются заданными

числами, а параметры - переменными.

В задачах нелинейного оценивания наиболее широкое применение

находят итеративные методы оптимизации. В большинстве нелинейных

задач находят применение метод линеаризации, метод наискорейшего

спуска, метод Маркварда.

В ПСП STATGRAPHICS используется метод Маркварда. Для

построения нелинейной модели необходимо выбрать программу

"Nonlinear Regression" раздела К.

После появления на экране меню, необходимо с помощью

преподавателя заполнить пустые окна. После этого нажать F6 и на

экране появятся результаты выполнения программы. Режим вывода

результатов на экран выбирается после нажатия клавиши F10.

Функция регрессии задается на языке APL (коэффициенты

регрессии обозначаются через PARM[1], PARM[2] и т.д.). Так,

например, функцию необходимо представить в

виде Y GETS EXP(PARM[1]*X1 + PARM[2]*X2)/(1 + PARM[3]*(X*X)).

Метод линеаризации представлен в [ ], метод наискорейшего

спуска в [ ], метод Маркварда в [ ].

5.6. Порядок выполнения работы и методические

указания по ее выполнению

Для оценки качества метода необходимо для одних и тех же

числовых последовательностей, имеющих различные статистические

характеристики и задаваемые преподавателем, построить зависимости

выходных параметров от входных, используя методы множественной,

пошаговой регрессии и гребневого анализа.

Порядок выполнения работ следующий:

1) запустить на выполнение программу STATGRAPHICS;

2) заполнить пустые поля, ввести набор исходных данных

одинаковой длины, используя раздел А "Data Management"; исходные

данные выдает преподаватель;

3) построить множественные модели, вида

и

используя программу "Multiple regression" (множественная линейная

регрессия) раздела К и провести интерпретацию результатов расчета;

4) построить модель методом включения и исключения, используя

программу "Stepwise variable Selection" (пошаговая регрессия)

раздела К и провести интерпретацию результатов;

5) построить модель с использованием гребневого анализа,

используя программу "Ridge Regression";

6) Построить нелинейную модель, используя программу "Nonlinear

Regression";

7) Провести сравнение методов обработки данных.

5.7. Содержание отчета

Каждый член бригады оформляет отчет, в котором приводит:

цели и задачи лабораторной работы;

назначение и краткую характеристику используемых программ;

последовательность построения модели множественной регрессии,

оценку значимости коэффициентов, оценку остатков, оценку

адекватности модели;

интерпретацию результатов;

вывод о проделанной работе.

5.8. Контрольные вопросы

1. Объяснить сущность метода множественной линейной регрессии

и пошагового регрессионного анализа, гребневого анализа, нелинейной

регрессии.

2. Каковы вычислительные процедуры пошагового регрессионного

анализа?

3. Каковы принципы интерпретации пошагового метода; гребневого

анализа?

4. Как проводится оценка значимости коэффициентов модели?

5. Как проводится оценка адекватности модели?

6. Как проводится сравнение моделей, полученных разными

методами?

60