1.3.1 Разложение сумм квадратов

В соответствии с основной идеей дисперсионного анализа разложим сумму S квадратов отклонений наблюдений от общего среднего на компоненты, отвечающие перечисленным факторам:

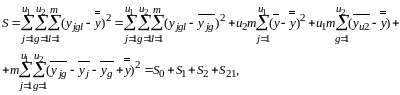(1.14)

где S - общая сумма квадратов, характеризущая рассеивание отдельных наблюдений y_jgl в общей совокупности за счёт влияния всех факторов;

S₀ - сумма квадратов отклонений ‘внутри серий’. Сумма характеризует рассеивание отдельных наблюдений за счёт влияния фактора случайности;

S₁ - сумма квадратов отклонений ‘между строками’. Сумма характеризует рассеивание средних по строкам в результате действия фактора случайности с дисперсией , фактора Х₁ с дисперсией d₁² и фактора взаимодействия с дисперсией среднего строки ;

S₂ - сумма квадратов отклонений ‘между строками’. Сумма характеризует рассеивание средних по столбцам в результате действия фактора случайности с дисперсией среднего столбца , фактора Х₂ (с дисперсией d₂² и фактора взаимодействия с дисперсией среднего столбца );

S₁₂ - сумма квадратов отклонений ‘между сериями’. Сумма S₁₂ характеризует рассеивание средних серий в результате действия фактора случайности с дисперсией среднего и фактора взаимодействия с дисперсией d₁₂².

1.3.2 Оценка дисперсий

Суммы квадратов S , S₀ , S₁ , S₂ , S₁₂ делённые каждая на соответствующее ей число степеней свободы n, n₀, n₁, n₂, n₁₂ дают несмещённые оценки дисперсии воспроизводимости d².

1. выборочная общая дисперсия по всем u₁u₂m наблюдениям

, (1.15)

с числом степеней свободы n = u₁u₂m-1,

2. выборочная дисперсия рассеивания ‘внутри серий’, или остаточная оценка является средневзвешенной дисперсией по всем сериям наблюдений:

, (1.16)

с числом степеней свободы n₀ = u₁u₂(m-1),

3. выборочная дисперсия рассеивания ‘между строками’:

, (1.17)

с числом степеней свободы u₁-1.

4. выборочная дисперсия рассеивания ‘между столбцами’:

, (1.18)

с числом степеней свободы n₂=u₁-1.

5. выборочная дисперсия рассеивания ‘между сериями’:

, (1.19)

с числом степеней свободы n₁₂=(u₁-1) (u₂-1).

Число степеней свободы проверяется по отношению n=n₀+n₁+n₂+n₁₂.

1.3.3 Оценка влияния факторов

Анализ значимости влияния факторов х₁, х₂ и их взаимодействия х₁₂ проводится по критерию Фишера при выбранном уровне значимости a в следующем порядке:

1. Влияние факторов х₁ и х₂ соответственно с дисперсиями:

, (1.20)

, (1.21)

признаётся значимым (d₁² > 0, d₂² > 0), если окажется значимым соответственно отличие S₁² от S₁₂² и S₂² от S₁₂² , то есть если соответствующий критерий:

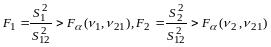. (1.22)

Если одно из этих дисперсионных отношений, то есть влияние соответствующего фактора, незначимо ( d₁² = 0 или d₂² = 0 ), то для дисперсии (d²+md₁₂²) мы получим две оценки S₁² ? S₁₂² или S₂² и S₁₂² соответственно, которые можно объединить в свободную оценку

S₁₂² = d²+md₁₂² с большим числом степеней свободы или .

Если оба фактора х₁ и х₂ незначимы (d₁² = 0, d₂² = 0 ), то оценки для дисперсии d²+md₁₂² можно объединить в свободную S₁₂² = d²+md₁₂² с большим числом степеней свободы .

2. влияние взаимодействия х₁₂ с дисперсией:

, (1.23)

признаётся значимым (d₁₂² > 0), если отличие S₁₂² и S₀² окажется значимым, то есть если критерий:

. (1.24)

В противном случае, то есть d₁₂²=0 и обе оценки S₁₂² и S₀² для d² можно объединить в одну с большим числом степеней свободы .

Если х₁,х₂ и х₁₂ значимы, то дисперсию воспроизводимости можно оценить выборочной общей дисперсией S².

Литература: [1, c.191-235; 5, c.145-189].

Контрольные вопросы:

1. Какова суть дисперсионного анализа?

2. Что вызывает влияние фактора Х (с дисперсией d_x²)?

3. Что характеризует сумма квадратов отклонений ‘между сериями’?

4. Какие можно дать приближённые оценки для дисперсии фактора Х?

5. Как оценить дисперсии в двухфакторном дисперсионном анализе?

6. По какому критерию проводится анализ значимости влияния факторов х₁, х₂ и их взаимодействия х₁₂ при выбранном уровне значимости a?

Лабораторная работа № 2.

Обработка экономической информации с помощью табличного процесса ‘EXCEL’

2.1 Цель работы

Краткий обзор возможностей программы EXCEL 7.0 для осуществления автоматизированной обработки экономической информации.

В результате выполнения лабораторной работы студенты должны уметь:

запускать программу Excel 7.0, строить электронные таблицы, вводить данные и редактировать их, задавать формулы, используя функции, производить анализ данных, получать графическое представление данных с помощью диаграмм, выводить данные на печатающее устройство.

2. Общие положения

Повсеместное использование программ обработки электронных таблиц обусловлено универсальными возможностями их применения. Электронные таблицы можно использовать как для решения простых задач учета, так и для составления различных бланков, деловой графики и даже полного баланса фирмы. Например, на предприятии с помощью электронных таблиц можно облегчить решение таких задач, как обработка заказов и планирование производства, расчет налогов и заработной платы, учет кадров и издержек, управление сбытом и имуществом и т.д.

Для работы Excel 7.0 необходима операционная система Windows 95. Запуск программы осуществляется активизацией команды Microsoft Excel в стартовом меню Programs или активизировать соответствующую кнопку в пиктографическом меню Панель Microsoft Office.

Построение таблицы Excel 7.0 выполняется в рабочем листе. Рабочий лист разделен на строки и столбцы, при этом пересечения строк и столбцов образуют ячейки, в которых, собственно, и содержится информация, представленная в рабочем листе. Рабочий лист состоит из 256 столбцов и 16384 строк. Excel 7.0 предоставляет возможность обработки данных непосредственно в самой ячейке. Ячейки вместе с содержимым можно перемещать и копировать. При перемещении ячейки её содержимое будет удалено из исходной ячейки и вставлено в указанную. При этом содержимое ячеек, в которые осуществляется перенос, автоматически удаляется. Во избежание этого, необходимо вставить пустые ячейки в ту область электронной таблицы, в которую Вы хотите перенести данные. С помощью операции копирования содержимое ячейки можно представить в рабочем листе дважды.

Чтобы одновременно переместить несколько ячеек, их следует предварительно выделить. Почти любая операция - будь то перемещение, копирование, удаление или форматирование - предполагает предварительное выделение ячеек. Две и более выделенных ячеек представляют собой интервал выделения или диапазон ячеек. Чтобы сделать ячейку активной, следует выполнить щелчок на этой ячейке.

В ячейке электронной таблицы может быть представлена информация различного типа: текст, числовые значения и формулы. При вводе данных Excel 7.0 автоматически распознаёт их тип. Ввод данных выполняется в активной ячейке. Чтобы вводимым данным не был автоматически присвоен один из заданных Excel 7.0 форматов, вводимую информацию следует предварять апострофом (‘). В результате введённые данные ( например, ‘i.i’ ) будут интерпретированы как текст и выровнены по левому краю. После удаления апострофа данные будут автоматически преобразованы в соответствующий формат. Если в ячейку вводится формула, то непосредственно после завершения ввода производятся вычисления, и результат вычислений отображается в ячейке. Формула может начинаться со знаков плюс (+), минус (-) и равно (=).

Если Вы хотите применить определенную команду или функцию к ячейкам, которые не примыкают друг к другу, то для маркировки этих ячеек следует использовать выделение несмежных диапазонов. Выделение несмежных диапазонов ячеек производится аналогично описанному выше процессу выделения смежных ячеек, но при этом следует держать нажатой клавишу [ Ctrl ]. Выделенные таким образом диапазоны ячеек нельзя перемещать или копировать. Однако выделение несмежных диапазонов ячеек можно использовать в случае удаления, форматирования или ввода данных.

Для выделения столбца необходимо выполнить щелчок на его заголовке. Чтобы выделить несколько смежных столбцов, следует поместить курсор мыши на заголовок первого выделяемого столбца и нажать левую кнопку манипулятора. Удерживая её нажатой, курсор мыши необходимо переместить до заголовка последнего выделяемого столбца. Для выделения строки с заголовком необходимо выполнить аналогичные действия.

Режим редактирования содержимого ячейки активизируется с помощью двойного щелчка на ячейке, после чего справа от содержимого ячейки будет представлен мерцающий курсор ввода. По умолчанию Excel 7.0 работает в режиме вставки. Если возникла необходимость работать в режиме замены, то следует нажать клавишу [ Insert ] и установить курсор мыши в нужную позицию.

Формула может содержать функции и математические операторы, порядок вычисления которых соответствует принятому в математике. В Excel 7.0 для нескольких ячеек, которые составляют интервал массива ( массив - интервал ), может быть задана одна общая формула-формула массива. Чтобы действие введенной формулы распространялось на весь массив, следует завершить её ввод нажатием комбинации клавиш [ Ctrl+Shift+Enter ]. Причем сама формула запишется в фигурных скобках, обозначающих формулу массива.

При копировании формулы автоматически изменяется и ссылка на ячейку. Для задания абсолютной ссылки используется знак доллара ( $ ). При последующем копировании формулы относительная ссылка в формуле будет изменяться, а абсолютная - нет.

В Excel 7.0 интегрирована экстраполирующая функция, т. е. функция, позволяющая автоматически продолжать заданные в табличном виде ряды данных ( прогрессии ). Она включает в себя функцию автозаполнения в сочетании с одной из специальных функций вычисления. Это может быть, например, функция вычисления арифметической прогрессии, при использовании которой каждое последующее значение вычисляется путем прибавления к предыдущему некоторого числа. Для этого, выделив диапазон ячеек, выберите команду @ Заполнить / Прогрессия из меню @ Правка. После этого на экране будет открыто диалоговое окно @ Прогрессия.

В вычислениях могут использоваться разнообразные формулы, служащие, к примеру, для определения синуса, среднего значения или размера годового амортизационных отчислений. Excel 7.0 предоставляет в распоряжение пользователя множество специальных функций, в которые эти формулы уже встроены. Указание значений, к которым должна быть применена та или иная функция, происходит путем задания аргументов. Способ задания функций всегда один и тот же, различие состоит только и количестве аргументов, которые должны быть указаны при задании функции :

=ИМЯ ФУНКЦИИ ( Аргументы ).

Чтобы легче было найти ошибку, можно установить режим отображения в ячейках формул вместо результатов вычислений, произведенных по этим формулам. Для этого следует установить в панели @ Вид диалогового окна @ Параметры опцию @ Формулы. Ширина столбцов будет при этом автоматически увеличена, чтобы обеспечить пользователю лучший обзор. Путём отмены опции @ Формулы в панели @ Вид диалогового окна @ Параметры можно снова включить режим показа результатов вычисления.

Excel 7.0 предоставляет в распоряжение пользователя различные функции для работы с диаграммами. На стадии создания и обработки диаграммы строка меню содержит специальные команды , с помощью которых реализуются эти функции. Можно воспользоваться также панелью инструментов Диаграмма, в которой в виде кнопок представлены наиболее важные команды. Эти функциональные возможности программы становятся доступными пользователю после активизации листа диаграммы в рабочей книге или выделения диаграммы, расположенной в рабочем листе.

Диаграмма может быть создана на отдельном листе. Однако её можно также создать как графический объект в рабочем листе и вывести на печать вместе с таблицей. Такая диаграмма будет сохраняться в документе вместе с другими элементами рабочей книги, в то время как диаграмма, созданная на отдельном листе, может быть сохранена в виде отдельного документа.

Перед активизацией Мастера диаграмм с помощью кнопки @ Мастера диаграмм в панели инструментов Стандартная необходимо выделить в рабочем листе диапазон ячеек, данные из которых должны быть представлены в диаграмме. Выделенный диапазон ячеек должен содержать ячейки с метками строк и столбцов, которые в последствии будут использованы в качестве меток оси и для легенды диаграммы.

После активизации Мастера диаграмм необходимо выделить область рабочего листа, в котором диаграмма будет вставлена как объект. Для этого с помощью мыши необходимо ‘ начертить ’ прямоугольник. Область, ограниченная этим прямоугольником, будет в дальнейшем использована для вставки диаграммы. После создания прямоугольника на экране появится первое диалоговое окно Мастера диаграмм. В данном диалоговом окне следует указать область, значения из которой будут использованы при построении диаграммы. Если Мастер диаграмм был активизирован после выделения области, содержащей данные, то в этом диалоговом окне будут автоматически представлены соответствующие адреса выделенного диапазона ячеек. Пользователь может одобрить предлагаемый диапазон ячеек или изменить его. Во втором диалоговом окне Мастера диаграмм можно выбрать тип диаграммы. Этот выбор не является окончательным : тип диаграммы можно будет впоследствии изменить.

Диаграммы одного и того же типа можно по-разному отформатировать. При этом следует выбирать формат, в наибольшей степени соответствующий цели построения диаграммы. В дальнейшем формат диаграммы также можно изменить.

В четвёртом диалоговом окне Мастера диаграмм Вашему вниманию будет представлен пример диаграммы выбранного типа и формата. В этом окне можно задать некоторые определяющие параметры для построения диаграммы. В последнем диалоговом окне Мастера диаграмм пользователь может указать, должна ли быть представлена в диаграмме легенда ( описание данных категории, которые представлены различными цветами ). После этого диаграмма будет вставлена в рабочий лист.

@Примечание: Создать в рабочем листе диаграмму можно также с помощью панели инструментов Диаграмма. Представьте на экране панель инструментов Диаграмма и выделите в таблице ячейки, содержимое которых должно быть представлено в диаграмме. Откройте палитру типов диаграмм, выберите нужный тип диаграммы и укажите с помощью мыши прямоугольную область, в которую должна быть помещена диаграмма. После того как Вы отпустите левую кнопку мыши, диаграмма будет создана с использованием установленного по умолчанию автоформата.

После изучения теоретических сведений и сдачи допуска каждая бригада получает у преподавателя номер варианта задания ( варианты даны ниже ). Необходимо разработать форму таблицы данных, количество строк и столбцов и их заголовки. Затем в среде EXCEL 7.0 реализовать эту таблицу.

2.3 Содержание отчета:

 название лабораторной работы;

 цель работы;

 задание на лабораторную работу;

 заполненная таблица текстовыми и числовыми данными, формулами;

 таблица, содержащая результаты вычислений;

 диаграмма;

 выводы по работе о целесообразности использования Excel 7.0 для решения такого класса задач.

Лабораторная работа № 3.

АНАЛИЗ И ПРОГНОЗИРОВАНИЕ ЭКОНОМИЧЕСКОЙ ИНФОРМАЦИИ В ВИДЕ ВРЕМЕННЫХ РЯДОВ С ИСПОЛЬЗОВАНИЕМ EXCEL 7.0.

3.1 Постановка задачи и цель работы

Последовательность наблюдений, упорядоченную во времени, будем называть временным рядом. Хотя возможно упорядочение и по какому-то другому параметру.

Основной чертой временных рядов по сравнению с другими видами статистического анализа, является существенность порядка, в котором производятся наблюдения.

Наблюдения, как правило, статистически зависимы и характер такой зависимости определяется положением наблюдений в последовательности.

Почти в каждой области встречаются явления, которые интересно знать и их изучать в их развитии и изменении во времени, например. Метеорологические условия, состояние здоровья, цена на той или иной товар, состояние производства в будущем и т. д.

Временной ряд может быть представлен в виде почасовой записи температуры, давления, расхода каких-либо технологических объектов или ежегодное количество смертных случаев, количество осадков, квартальные данные о валовом национальном продукте и т. д.

Цели изучения временных рядов могут быть следующие:

1. предсказать будущее на основании знания прошлого;

2) управлять процессом, порождающим ряд;

3) выяснить механизм, порождающий ряд, или просто сжато описать характерные особенности ряда;

4) на основании ограниченного количества информации, которая содержится во временном ряду конечной длины, сделать вывод о вероятностном механизме, порождающем этот ряд, анализировать структуру, лежащую в его основе.

В самом общем случае математическую модель временного ряда можно представить в виде

(3.1)

В (3.1) имеется равноотстоящих чисел , - детерминированная последовательность ( систематическая составляющая ); - случайная последовательность.

Модель (1) может рассматриваться в нескольких вариантах, а именно, влияние времени может сказываться либо на , либо на , либо на обеих компонентах. Временные последовательности часто называют трендом. Функция может быть представлена медленно меняющейся функцией времени, например, полиномом достаточно низкой степени. Или циклической последовательностью, например, конечным отрезком ряда Фурье.

Одной из общих моделей, в которой влияние временного параметра проявляется в случайной составляющей, является стационарный случайный процесс, а именно процесс авторегрессии, и

является стохастическим разностным уравнением первого порядка. В этой модели оказывает влияние на и все последующие .

Наилучшим прогнозом ( в смысле минимума среднеквадратической ошибки ) будет

Влияние времени может быть представлено в (3.1) так, что систематическая составляющая является трендом во времени, а случайная составляющая образует стационарный случайный процесс. К примеру экономический временной ряд может складываться из долговременного и сезонного изменений, которые вместе составляют , и из колебательной компоненты и других нерегулярностей, которые вместе образуют и могут быть описаны процессом авторегрессии.

В тех случаях, когда тренд имеет вполне определённую структуру и определяется конечным числом параметров, мы рассматриваем задачи статистических выводов о значениях этих параметров. То есть рассматриваются задачи о степенях и количестве слагаемых, включаемых в модель.

Если тренд не описывается точно, то для его оценивания можно использовать непараметрические методы, такие, как сглаживание.

Если случайный процесс описывается с помощью конечного числа параметров, как процесс авторегрессии, то здесь возникают задачи оценки коэффициентов, проверки гипотез относительно их значений или решения вопроса о том, какого порядка процесс следует использовать. Здесь же необходимо решать вопросы о проверке статистических гипотез.

Значительную часть статистических методов, используемых при анализе временных рядов, представляют методы регрессионного анализа или его модификации.

Независимые переменные могут быть заданы функциями времени, например, степенями переменной или тригонометрическими функциями от .

Часто используются модели, в которых подлежащий изучению тренд с течением времени гладко возрастает или убывает. В этом случае используют для описания тренда полиномы. Полином первой степени отражает равномерное во времени возрастание или убывание значений ряда. Полином второй степени может выражать тенденцию возрастания и последующего убывания значений ряда и т. д.

Целью настоящей работы является ознакомление с методами анализа временных последовательностей ( метод скользящего среднего, экспоненциального сглаживания, метод Бокса - Дженкинса, регрессионного анализа ) и их применения для предсказания некоторых случайных временных рядов.

Систематическую составляющую часто представляют в виде полинома порядка :

(3.2)

Кроме полиномиальных возможны и другие виды моделей (3.2).

Задача предсказания значения отстоящего на шагов от последнего значения , включает несколько этапов:

1) Выбор дискретности **** наблюдений и интервала наблюдения ;

2) Выбор модели процесса, т. е. определение характера изменения систематической составляющей ;

3) Вычисление оценок коэффициентов модели по значениям, наблюдаемым на интервале с дискретностью ;

4) Использование полученной модели для предсказания значения ;

5) Оценка точности предсказания.

3.2 Метод скользящего среднего

Пусть имеется ряд значений , наблюденных на интервале времени с дискретностью .

Искомая модель задана в виде полинома степени , коэффициенты которого неизвестны.

Для получения оценок неизвестных коэффициентов целесообразно использовать сглаживание. Наблюдения включают в себя шум и тогда для текущего -го наблюдения простейшую модель представим в виде

,

где - шум с нулевым математическим ожиданием.

Пусть изменяется достаточно медленно, т. е. в интервале, внутри которого производится предсказание, модель процесса будет постоянной.

Для оценки можно использовать метод наименьших квадратов, который в случае постоянной модели превращается в метод скользящего среднего. Согласно этому методу, среднее из наблюдений, вычисленное для интервала , определяется по формуле

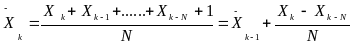(3.3)

Для вычисления среднего необходимо вычислить и запомнить данных.

3.3 Метод экспоненциального сглаживания

Для сокращения объёма информации можно вместо величины ( самого раннего наблюдения ) воспользоваться оценкой этой величины, равной среднему, вычисленному для предыдущего интервала :

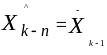(3.4)

Подставив в выражение (3.3) вместо величину , получим

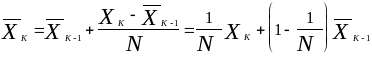(3.5)

Для вычисления (3.5) необходимо только значение предыдущей величины ( среднего, вычисленного в момент на основании последних наблюдений ).

Обозначим через .Очевидно, что .

Тогда

(3.6)

Если вместо предыдущей сглаженной величины подставить её выражение через ещё более ранние величины, то получим

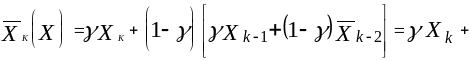
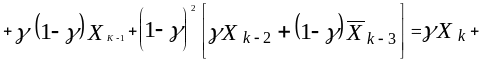
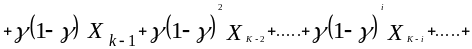
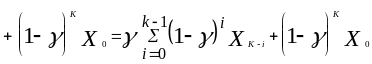. (3.7)

Из выражения (3.7) видно, что функция является линейной комбинацией всех прошлых наблюденных значений. Веса, приписываемые этим значениям, уменьшаются с ‘возрастом’ данных в геометрической прогрессии. Операция, производимая над любым рядом данных согласно формуле (3.6), называется экспоненциальным сглаживанием.

В интегральной форме оператор экспоненциального сглаживания представляется в следующем виде

,

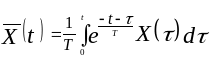где - параметр сглаживания.

Если к результату простого экспоненциального сглаживания вновь применить тот же метод, получим оператор сглаживания второго порядка

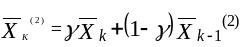(3.8)

Двойное сглаживание можно применить для определения коэффициентов модели.

Аналогично можно определить оператор сглаживания третьего порядка

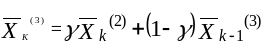
В общем случае для многократного экспоненциального сглаживания

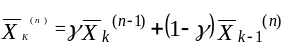
Выразим текущие сглаженные величины через текущие наблюденные значения и предыдущие сглаженные величины

,

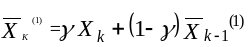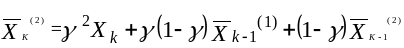
Выразим коэффициенты модели через сглаженные величины. Для этого необходимо записать выражения для сглаженных величин через оценки коэффициентов и

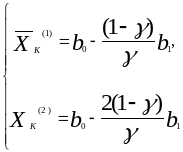(3.9)

Решив систему (3.9) относительно и , получим

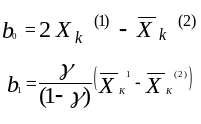(3.10)

Подставив (3.8) в (3.10), получим

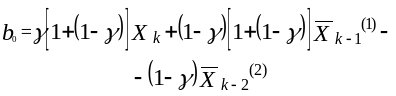
(3.11)

По аналогии с (3.9 ), запишем выражения для предыдущих сглаженных величин через оценки коэффициентов модели

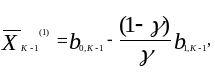
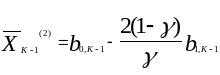(3.12)

Подставив (3.12) в уравнение (3.11), получим окончательное выражение для оценок коэффициентов линейной модели первой степени

,

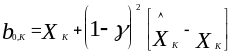
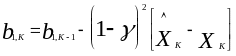где .

Для квадратичной модели вида , расчетные формулы для оценок коэффициентов b ₀ , b ₁ , b ₂:

где .

Интервал дискретности выбирается в зависимости от требуемого минимального времени упреждения.

Обычно берут интервал между замерами , равным минимального времени упреждения.

После того, как получены оценки коэффициентов модели, может быть вычислена оценка величины будущего наблюдения

,

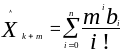где - порядок полинома;

- оценка коэффициентов ;

- количество интервалов от последнего наблюденного значения до предсказанного значения .

Порядок выполнения работы

Необходимо оценить прогнозируемую величину производительности труда ( задача №1 ) или величину прибыли ( задача №2 ), используя данные по задаче 1и 2:

1. Ввести исходные данные

2. Порядок работы с Excel смотри бизнес анализ стр. 173.для скользящего среднего.

3. Для функции регрессии.

4. Экспоненциальное сглаживание.

5. Метод Бокса- Джен.

Лабораторная работа № 4

Обработка статистической информации с использованием регрессионного анализа.

4.1 Цель работы

Изучить методы проведения статистической обработки информации при построении статических моделей технологических процессов для определения класса объекта; ознакомиться с назначением, предпосылками применения и вычислительным алгоритмом линейного регрессионного анализа (РА), приобрести практические навыки общения пользователя с персональными ЭВМ типа IBM PC, а также ознакомиться с принципами работы пакета статистических программ (ПСП) STATGRAPHICS, используемого для обработки статистической информации.