1.2.1 Разложение суммы квадратов

Разложим сумму g квадратов отклонений наблюдений от общего среднего на две составляющие суммы, одна из которых будет характеризовать влияние фактора случайности, а вторая - фактора изменчивости Х.

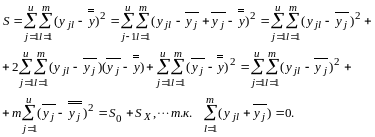(1.4)

Дисперсия, характеризующая рассеивание наблюдений в результате действия обоих факторов как случайности (с дисперсией d₀² ), так и изучаемого Х (с дисперсией d_x² ) представлена в виде:

. (1.5)

Сумма квадратов отклонений ‘внутри серий’, характеризующая остаточное рассеивание случайных погрешностей внутри опыта, то есть их воспроизводим ость (с дисперсией d₀²):

(1.6)

Сумма квадратов отклонений ‘между сериями’.

(1.7)

Сумма характеризует рассеивание средних серий за счёт случайных причин (с дисперсией для средних серий) и исследуемого фактора (с дисперсией d_?²).

1.2.2 Оценка дисперсий

Пусть влияние Х на Y отсутствует, то есть нуль гипотеза об однородности верна. Тогда все серии параллельных наблюдений можно рассматривать как случайные выборки из одной и той же нормальной совокупности и, следовательно:

1. Несмещённая оценка дисперсии воспризводимости d₀² по всем um наблюдениям определяется выражением:

, (1.8)

с числом степеней свободы um-1.

2. Выборочная дисперсия рассеивания ‘внутри серий’ или остаточная оценка дисперсии воспризводимости d² находится как среднее из выборочных дисперсий по каждой серии в отдельности

. (1.9)

3. Выборочная дисперсия рассеивания между средними серий служит несмещённой оценкой дисперсии , с которой нормально распределены независимые друг от друга средние серии:

, (1.10)

с числом степеней свободы V_x=u-1.

Таким образом, S₀ и S_X независимы друг от друга.

При отсутствии влияния фактора Х выборочные оценки S_XS_X S_X однородны, так как являются оценками одной и той же генеральной дисперсии d².

Предположим теперь, что влияние фактора Х на выходной параметр существенно, то есть нуль гипотеза об однородности не верна. Тогда серии параллельных наблюдений можно рассматривать как случайные выборки с одной и той же дисперсией d₀² и различными центрами распределения С₁,....,С_j,.....,C_u и, следовательно:

1) выборочная дисперсия d² характеризует влияние как фактора случайности, так и фактора Х, то есть d²=d₀²+d_?²;

2. поскольку S₀ не изменяется при замене y_jl на y_jl- y_j, то выборочная дисперсия S₀² также не изменяется и по-прежнему является несмещённой оценкой для d², то есть S₀² » d²;

3)поскольку сумма S_X учитывает не только случайные, но и систематические расхождения между средними серий и увеличивается за счет влияния фактора Х, то дисперсия при этом также увеличивается и перестаёт служить оценкой только для , то есть , откуда S_x² » d²+md_x²;

4) независимость S₀ и S_X друг от друга сохраняется.

Таким образом, для дисперсии фактора Х можно дать две приближённые оценки d_x² » d²- d₀² » d²- d₀² ,

Первая оценка менее точна из-за погрешностей величин S² и S₀². Точность же второй выше, так как дисперсии входят в неё, делённые на m. Из этого очевидно, что при влиянии фактора Х выборочной оценки S², S₀², S_?² неоднородны. Сопоставляя эти выборочные дисперсии, можно принять решение о справедливости первого или второго предположения относительно значимости влияния фактора Х (с дисперсией d_x²) на выходной параметр.