4.3. Признак Коши

_{Теорема 1. Если для ряда с положительными членами}

_(6.63)

_{1) можно указать такое, не зависящее от n, число q больше нуля и меньше единицы (0 < q < 1), что для всех n > v выполняется неравенство}

_(6.64)

_{то ряд (6.63) сходится; 2) если же при всех n > v выполнено неравенство}

_(6.65)

_{то ряд (6.63) расходится.}

_{Доказательство. Сначала предположим, что выполняется неравенство (6.64). Возвышая его в степень n, получаем, что}

_(6.66)

_{при всех n > v. Далее, сравним ряд (6.63) с рядом}

_(6.67)

_{и докажем, что они удовлетворяют условиям теоремы 3 (гл.6, §4, п.4.1).}

_{Действительно, ряд (6.67) является геометрической прогрессией, знаменатель q которой удовлетворяет неравенству 0 < q < 1, а потому ряд (6.67) сходится. Кроме того, члены ряда (6.63), начиная с v, то есть при n > v, не больше соответствующих членов ряда (6.67), как это следует из неравенства (6.64). Значит по теореме 3 (гл.6, §4, п.4.1) ряд (6.63) сходится.}

_{Теперь предполагаем, что выполнено неравенство (6.65). Возвышая его в степень n, находим, что при всех n > v}

_(6.68)

_{а потому, для ряда (6.63) не выполнен необходимый признак сходимости, так как из (6.68) заключаем, что . Следовательно, ряд (6.63) расходится. Теорема доказана.}

_{Признак Коши можно представить в более удобной для применений форме – в виде предельного равенства.}

_{Теорема 2. Если для ряда с положительными членами}

_(6.69)

_{существует предел то, если:}

_{1) 0 ≤ ℓ < 1, тогда ряд (6.69) сходится;}

_{2) ℓ > 1, тогда ряд (6.69) расходится;}

_{3) ℓ = 1, тогда при помощи признака Коши решить вопрос о сходимости ряда (6.69) нельзя, за исключением того случая, когда стремится к пределу равному 1 справа. В этом случае ряд (6.69) расходится.}

_{Доказательства этой теоремы аналогично доказательству теоремы 2 (гл.6, §4, п.4.2) для признака Даламбера. Нужно только в доказательстве заменить через .}

_{Кроме этого можно доказать также, что если предел в правой части существует. Но бывают такие случаи, когда существует предел в левой части, но предел в правой части не существует. Отсюда заключаем, что признак Коши в форме предельного равенства распространяется на большее количество случаев, чем признак Даламбера в форме предельного равенства.}

_{Рассмотрим пример на применение признака Коши.}

_{Пример. Исследовать ряд .}

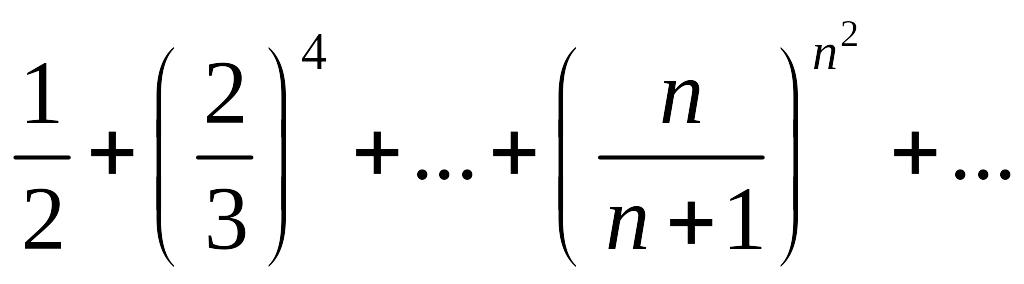_{Здесь 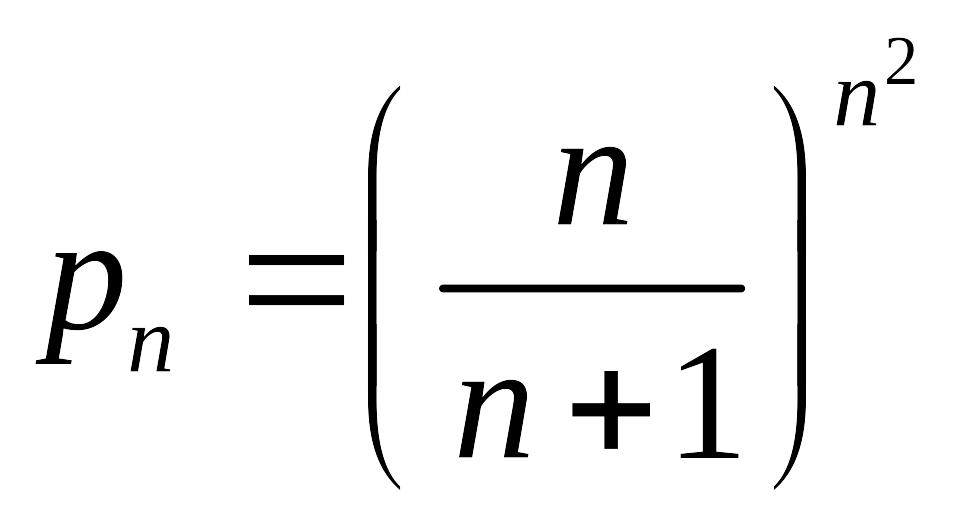и потому .}

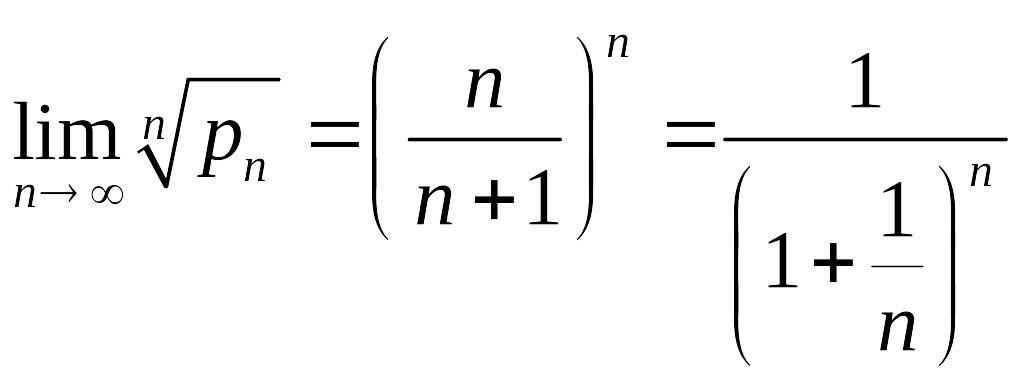_{Далее применяем признак Коши в форме предельного равенства}

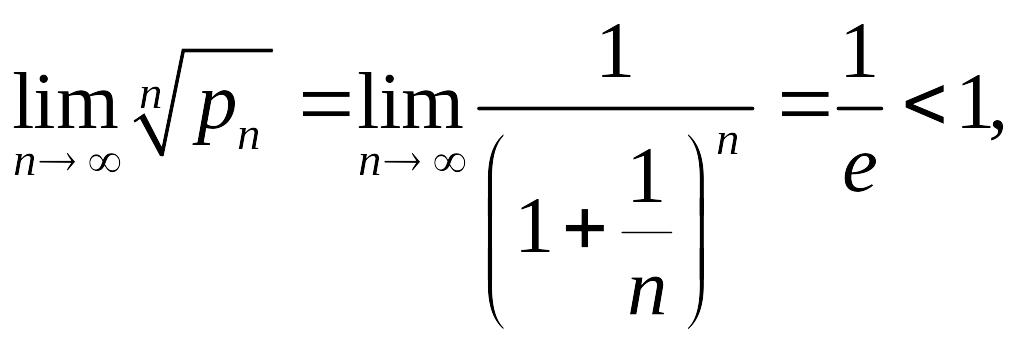
_{а потому ряд сходится.}

4.4. Интегральный признак сходимости или расходимости ряда

_{Теорема. Пусть дан ряд с положительными членами}

_(6.70)

_{и функция f(x), причем: 1) члены ряда убывают и}

_{2) функция f(x) непрерывна и убывает в промежутке и, кроме того, она такая, что .}

_{Тогда если}

_{(С – конечное число), (6.71)}

_{то ряд (6.70) сходится; если же}

_{, (6.72)}

_{то ряд (6.70) расходится.}

_{Другими словами: ряд (6.70) сходится либо расходится вместе с несобственным интегралом}

_{Доказательство. В прямоугольной системе координат хОу отметим на оси Ох точки x = 1, x = 2,…, x = n,… (рис.68). В этих точках проведем ординаты, соответственно, равные членам ряда р1, р2,..., рn…. Построим также график функции y = f(x), который по условию теоремы пройдет через вершины проведенных ординат.}

_{Рис. 68}

_{Далее на сегменте 1 ≤ x ≤ 2 приняв его за основание, построим два выходящий и входящий прямоугольника соответственно с высотами p1 и p2.}

_{Точно также на сегменте 2 ≤ x ≤ 3, приняв его за основание, построим два выходящий и входящий прямоугольника соответственно с высотами p2 и p3.}

_{Продолжая эти построения, переходим, наконец, к сегменту n – 1 ≤ x ≤ n, и приняв его за основание, построим два выходящий и входящий прямоугольника соответственно с высотами pn–1 и pn.}

_{Так как основания всех этих прямоугольников равны 1, то их площади численно равны высоте соответствующего прямоугольника.}

_{Из рис.68 заключаем, что криволинейная трапеция PABQ, ограниченная снизу отрезком [1,n] оси Ox, сверху графиком функции y = f(x), а с боков двумя ординатами в точках x = 1 и x = n, имеет площадь равную Эта площадь меньше суммы площадей выходящих прямоугольников, т.е.}

_(6.73)

_{Кроме того, площадь криволинейной трапеции PABQ больше суммы площадей входящих прямоугольников}

_{. (6.74)}

_{Обозначим через Sn усеченную сумму порядка n ряда (6.70)}

_{Тогда, прибавляя к обеим частям (6.73) рn, получим}

_{. (6.75)}

_{Если же прибавить к обеим частям (6.74) р1, то найдем}

_{. (6.76)}

_{Предположим теперь, что выполнено предельное равенство (6.71) и докажем, что ряд (6.70) сходится.}

_{Действительно, так как при , ,то при увеличении n интеграл возрастает, а потому при любом натуральном n выполнено неравенство С помощью этого неравенства и неравенства (6.76) находим, что при любых натуральных n. Значит последовательность усеченных сумм ряда с положительными членами (6.70) ограничена, а потому ряд (6.70) сходящийся.}

_{После этого предположим, что выполнено предельное равенство (6.72). Тогда из (6.75) заключаем, что левая часть этого неравенства, а подавно и правая часть неограниченно увеличиваются, т.е. Следовательно, ряд (6.70) расходится. Теорема доказана.}

_{Из приводимых ниже примеров следует, что интегральный признак в состоянии решить вопрос о сходимости или расходимости ряда в тех случаях, когда признаки, основанные на сравнении, признак Даламбера, или признак Коши сделать этого не могут.}

_{Пример 1. Применим интегральный признак к рассмотренному уже гармоническому ряду .}

_{Подберем сначала функцию f(x). В этом примере функция f(x) должна удовлетворять равенствам , для всех n = 1,2,… Поэтому для функции f(x) можно взять , которая непрерывна и убывает при}

_{Составим интеграл . Затем находим предел , а потому гармонический ряд расходится.}

_{Заметим, что применение признака Даламбера не дало бы ответа на вопрос о характере сходимости гармонического ряда. В самом деле, здесь и . То же самое имеем в результате применения признака Коши.}

Пример 2. Исследовать ряд

(6.77)

причем полагаем α > 0 и считаем , так как случай α = 1 был рассмотрен в предыдущем примере (гармонический ряд).

Применим интегральный признак. В этом примере функция f(x) должна удовлетворять условию _. Поэтому можно положить тогда эта функция непрерывна и убывает при , а потому удовлетворяет условиям интегрального признака.

Вычислим интеграл

_.

Пусть α > 1, тогда

Значит при α > 1 ряд (6.77) сходится.

Далее, считаем α < 1, тогда α – 1 < 0, , где 1– α > 0 и

_.

Это означает, что при α < 1 ряд (6.77) расходится.

Наконец, если , то невыполнен необходимый признак сходимости, а потому ряд (6.77) расходится.

Итак, ряд (6.77) сходится только при α > 1; при ряд (6.94) расходится.

Пример 3. Исследовать ряд

(6.78)

Не трудно проверить, что признак Даламбера не может решить вопрос о поведении данного ряда. Для применения интегрального признака нужно найти такую функцию f(x), для которой выполнено равенство .

Поэтому функцию f(x) можно определить равенством .

Выбранная функция f(x) непрерывна и убывает при , при x = 1 она имеет разрыв. Так как начальные члены ряда не влияют на поведение ряда, также как и значения функции f(x) в начале промежутка не влияют на сходимость несобственного интеграла , то рассмотрим интеграл Отсюда имеем это означает, что ряд (6.78) расходится.

На этом закончим изложение теории рядов с положительными членами и перейдем к рядам с произвольными членами.