§3. Числовые Ряды с положительными членами

Для того, чтобы применить какой-нибудь ряд для решения практического вопроса, нужно, прежде всего, доказать, что он сходящийся. Проще всего сходимость или расходимость может быть установлена для рядов с членами одного знака. Далее будет доказано, что исследование сходимости рядов с членами различных знаков (положительными или отрицательными) чаще всего может быть сведено к исследованию сходимости другого ряда, но с членами одного знака. По этой причине, прежде всего, нужно исследовать сходимость и расходимость рядов с членами одного знака. Для определенности будем рассматривать ряд с положительными членами. Поскольку ряд с отрицательными членами сводится к положительному ряду путем умножения отрицательного ряда на число –1, что согласно теореме 3, §2, не влияет на сходимость ряда.

Будем обозначать через положительные числа, а ряд с положительными членами будет записывать в виде

. (6.26)

Из рассмотрения усеченных сумм ряда (6.26): , , ,…,  …. Можно заключить, что последовательность усеченных сумм ряда с положительными членами – возрастающая: . Поэтому здесь возможны два и только два следующих случая:

1) последовательность неограниченна сверху и тогда, а это означает, что ряд (6.26) собственно расходится;

2) последовательность ограничена сверху и в таком случае она, будучи возрастающей и ограниченной, имеет конечный предел и поэтому ряд (6.26) сходится.

Этими двумя случаями исчерпываются всевозможные ряды с положительными членами. Отсюда можно заключить, что ряды с положительными членами не могут быть осциллирующими.

Из изложенного получается следующий необходимый и достаточный признак сходимости ряда с положительными членами: для сходимости ряда с положительными членами необходимо и достаточно, чтобы последовательность его усеченных сумм была ограниченной.

В последующем этот признак будет неоднократно использован при установлении других практически удобных для применения достаточных признаков сходимости и расходимости рядов с положительными членами.

§4. ДостаточныЕ признакИ сходимости и расходимости рядов с положительными членами.

4.1 Признаки, основанные на сравнении двух рядов

Определение. Пусть все элементы ряда с положительными членами

(6.27)

не больше соответствующих элементов второго ряда с положительными членами

(6.28)

то есть выполняются неравенства , тогда ряд (6.28) называется мажорантным рядом или мажорантой для ряда (6.27). В свою очередь (6.27) называется минорантным рядом или минорантой для ряда (6.28).

Теорема 1. Даны два ряда с положительными членами

(6.29)

(6.30)

тогда если: 1) , 2) ряд (6.30) сходится и имеет сумму , то сходится и ряд (6.29).

Эту теорему можно сформулировать еще и следующим образом – если мажоранта исследуемого ряда сходится, то и исследуемый ряд сходится.

Доказательство. Введем обозначения усеченных сумм ряда (6.29) и (6.30)

Согласно условию 2) теоремы 1, имеем . Отсюда, так как последовательность стремится к пределу , возрастая, заключаем, что при любых натуральных n выполнено неравенство

(6.31)

Далее, складывая неравенства условия 1) теоремы 1, получаем

и на основании введенных обозначений, а также (6.31), имеем при любых натуральных n. Следовательно, последовательность ограничена, а это означает, что ряд (6.29) сходится. Теорема доказана.

Теорема 2. Даны два ряда с положительными членами

(6.32)

(6.33)

тогда если 1) , 2) ряд (6.33) расходится, то ряд (6.32) расходится.

Другими словами если миноранта исследуемого ряда расходится, то и исследуемый ряд расходится.

Доказательство. Обозначим усеченные суммы ряда (6.32) и (6.33)

По условию 2) теоремы 2 − . Вследствие условия 1) теоремы 2 имеет место неравенство , а это означает, что и . Следовательно, ряд (6.32) расходится. Теорема доказана.

Последние две теоремы можно высказать в более общей форме. Эти обобщения даны в следующих двух теоремах.

Теорема 3. Даны два ряда с положительными членами

(6.34)

(6.35)

тогда если: 1) все члены ряда (6.34), начиная с некоторого v, не больше соответствующих членов ряда (6.35), то есть, при всех n > v, выполнено неравенство

, (6.36)

2) ряд (6.35) сходится, то сходится и ряд (6.34).

Доказательство. Отбрасывая в рядах (6.34) и (6.35) первые v членов, которые не удовлетворяют неравенству (6.36), получим следующие два ряда.

(6.37)

(6.38)

Сходимость ряда (6.35) распространяется по теореме 4 (гл.6, §2) на ряд (6.38), так как последний ряд получается из ряда (6.35) отбрасыванием конечного числа начальных членов .

Сходящийся ряд (6.38) является мажорантой для ряда (6.37), а потому по теореме 1 ряд (6.37) также сходится. Но, приписав в начале ряда (6.37) конечное число членов , получим ряд (6.34), который сходится по только что упомянутой теореме 4 (гл.6, §2). Теорема доказана.

Теорема 4. Даны два ряда с положительными членами

(6.39)

(6.40)

тогда, если: 1) все члены ряда (6.39), начиная с некоторого v, не меньше

соответствующих членов ряда (6.40), то есть при всех n > v, выполнено неравенство ,

2. ряд (6.40) расходится, то расходится и ряд (6.39).

Доказательство. Отбрасывая в рядах (6.39) и (6.40) первые v членов получаем еще два ряда

(6.41)

(6.42)

Расходимость ряда (6.40) распространяется по теореме 4 (гл.6, §2) на ряд (6.42), так как этот ряд получается из (6.40) отбрасыванием конечного числа начальных членов . Значит ряд (6.42) расходится и является (по условию 1)) минорантой ряда (6.41), а тогда по теореме 2 (гл.6, §4, п.4.1) ряд (6.56) расходится. Но ряд (6.39) получается из ряда (6.41), если в начале последнего ряда приписать члены , а потому по теореме 4 (гл.6, §2) ряд (6.39) расходится. Теорема доказана.

В следующих двух теоремах признаки сходимости и расходимости, основанные на сравнении двух рядов, даны в форме предельных равенств. Заметим, что в форме предельных равенств эти признаки является весьма удобными для применений.

Теорема 5. Если ряды с положительными членами

, (6.43)

. (6.44)

таковы, что: 1) существует конечный предел

, (6.45)

2. ряд (6.44) сходится, то тогда сходится и ряд (6.43).

Доказательство. Предельное равенство (6.45) означает, что по теореме 2 (гл.1, §5, п.5.2) последовательность ограничена. Следовательно, можно

указать такое число M > 0, что все элементы последовательности удовлетворяют неравенству . Умножая это неравенство на , получим

. (6.46)

После этого сравним между собой три ряда: (6.43), (6.44) и ряд

. (6.47)

Так как ряд (6.44) сходится, то по теореме 3 (гл. 6, §2) сходится и ряд (6.47). Но в силу неравенства (6.46) сходящейся ряд (6.47) является мажорантой для ряда (6.43). Следовательно, для рядов (6.43) и (6.47) выполнены все условия теоремы 1 (гл.6, §4, п.4.1) и потому ряд (6.43) сходится. Теорема доказана.

Теорема 6. Если ряды с положительными членами

, (6.48)

(6.49)

таковы что: 1) существует положительный предел (конечный или бесконечный)

, (6.50)

2) ряд (6.49) расходится, то тогда расходится также и ряд (6.48).

Доказательство. В начале рассмотрим случай, когда число конечное . Тогда, согласно определению предела последовательности, для любого положительного числа можно указать такое натуральное число v, что при всех n > v выполнено неравенство . Полагая здесь приходим к неравенству . Отсюда, умножая на , имеем (при всех n > v).

Теперь сравним между собой три ряда: (6.48), (6.49) и ряд

. (6.51)

В согласии с дополнительным замечанием к теореме 3 (гл.6, §2); из расходимости ряда (6.49) следует расходимость ряда (6.51). Тогда ряды (6.48) и (6.51) удовлетворяют условиям теоремы 4 (гл.6, §4, п.4.1) и потому ряд (6.48) расходится.

Теперь обратимся к случаю, когда . Предельное равенство означает, что каким бы ни было положительное число λ, всегда можно указать такое натуральное число v, что при всех n > v выполнено неравенство и, умножая это неравенство на , получим при всех n > v. Далее доказательство, точно такое же, как и для случая конечного . Теорема доказана.

Рассмотрим примеры, иллюстрирующие признаки сравнения.

Пример 1. Исследовать ряд

. (6.52)

Сравним этот ряд со сходящимся рядом (пример 1, гл.6, §1)

.

В соответствии с теоремой 5 (гл.6,§4, п.4.1) здесь

тогда

Так как , значит ряд (6.52) сходится.

Пример 2. Исследовать ряд

. (6.53)

Сравниваем ряд (6.53) с гармоническим (расходящимся) рядом и применяем теорему 6 (гл.6, §4, п.4.1). Здесь и потому

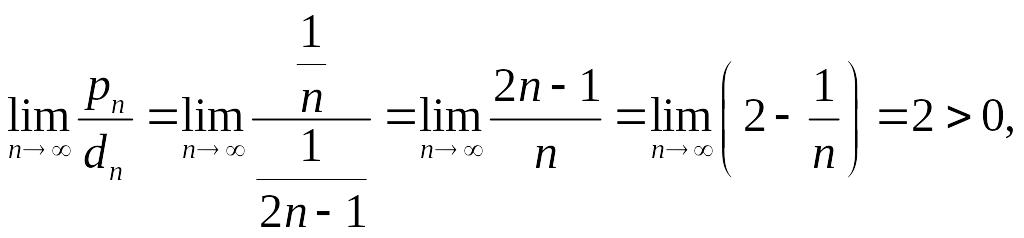
а потому ряд (6.53) расходится.