§2. Общие свойства числовых бесконечных рядов

Теорема 1. (Необходимый признак сходимости ряда) Если бесконечный ряд сходится, то при его общий член стремится к нулю,

(6.10)

Доказательство. Так как ряд сходится, то это означает, что его усеченная сумма стремится к конечному пределу , но , а потому

Теорема доказана.

Замечание. Условие (6.10) является лишь необходимым условием сходимости ряда, но оно не достаточное для того, чтобы утверждать сходимость ряда. В самом деле, рассмотрим гармонический ряд здесь общий член ряда стремится к нулю , но как было доказано в предыдущем разделе (пример 2) гармонический ряд собственно расходится.

Таким образом, если известно, что , то на основании этого предельного равенства никаких заключений о сходимости или расходимости ряда сделать нельзя. Ряд может быть либо сходящимся, либо расходящимся.

Но если известно, что не существует, либо существует, но не равен нулю то в этом случае, можно утверждать, что ряд расходится. Последнее замечание будет неоднократно использовано в последующем.

Теорема 2. Даны два любых сходящихся ряда

(6.11)

(6.12)

тогда ряд, полученный почленным сложением этих двух рядов

(6.13)

также сходится и имеет сумму .

Доказательство. Введем обозначения для усеченных сумм

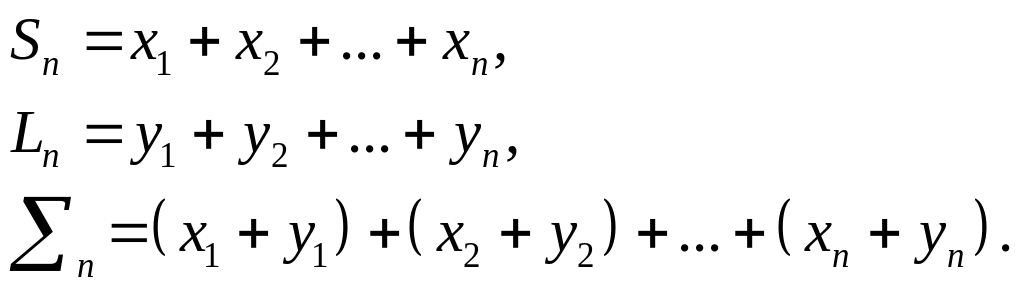
По условию теоремы дано, что

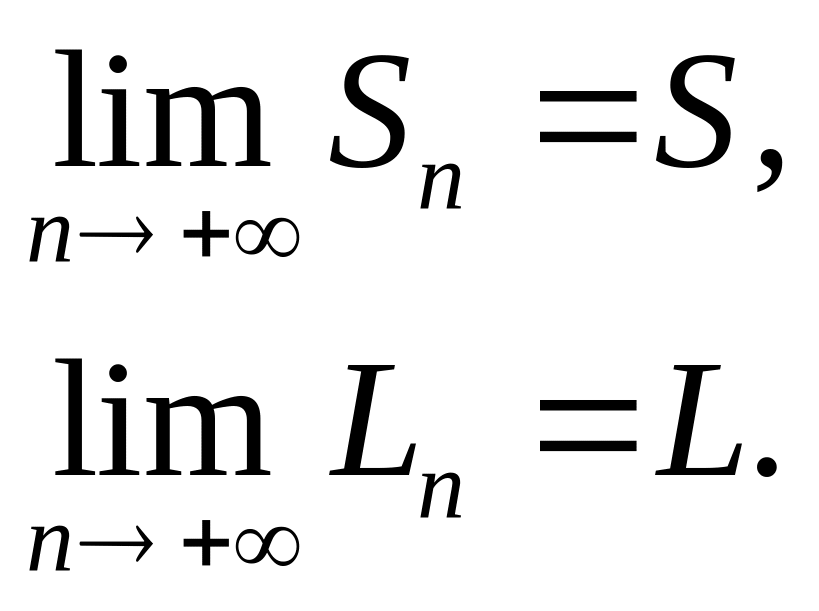
Кроме того, имеем

а потому Отсюда находим

Итак, а это означает, что ряд (6.13) сходится и имеет сумму равную .

Поэтому сходящиеся ряды можно почленно складывать. Аналогичными рассуждениями легко доказать, что ряд, полученный почленным вычитанием сходящихся рядов (6.11) и (6.12) также сходится и имеет сумму, равную , то есть сходящиеся ряды можно почленно вычитать.

Теорема 3. Если в сходящемся ряде все его члены умножить на одно и тоже число , то полученный при этом ряд

(6.14)

сходится и имеет сумму, равную .

Доказательство. Введем обозначения для усеченных сумм порядка n

По условию теоремы имеем . Простые преобразования суммы дают

Далее Значит, доказано, что а потому ряд (6.14) сходится и имеет сумму, равную .

Заметим, что доказанная теорема 3 является распространением на сходящиеся ряды известного свойства арифметических сумм о возможности вынесения общего множителя слагаемых этой суммы за знак скобки.

Замечание. Если ряд

(6.15)

расходится и любое число не равное нулю, , то ряд

(6.16)

также расходится.

В самом деле, сохраняя те же обозначения для усеченных сумм, как и прежде, имеем

. (6.17)

Если ряд (6.15) собственно расходящийся, то и из (6.17) следует, что , а потому (6.16) также есть собственно расходящийся ряд.

Если же ряд (6.15) осциллирующий, то есть, не существует, то из (6.17) заключаем, что не существует и . Отсюда заключаем, что ряд (6.16) осциллирующий.

Теорема 4. Сходимость или расходимость ряда

(6.18)

не нарушится, если отбросить любое конечное число начальных членов этого ряда или приписать в начало этого ряда любое конечное число новых членов.

Доказательство. Пусть k, произвольно взятое натуральное число, которое в дальнейшем считается постоянным. Отбрасывая в ряде (6.18) первые k членов получим ряд

. (6.19)

Введем обозначение усеченной суммы ряда (6.19) порядка n

(6.20)

Обозначим через С сумму всех k отброшенных членов

(6.21)

Заметим, что С является постоянным числом. Сложим равенства (6.20) и (6.21)

_. (6.22)

Правая часть равенства (6.22) представляет собой усеченную сумму ряда (6.18) порядка n + k , следовательно, или .

Если ряд (6.18) сходится, то это означает, что существует конечный предел , равный сумме ряда S: . Отсюда заключаем, что справедливо также предельное равенство, а это значит, что ряд (6.19) сходится и имеет сумму .

Далее предположим, что ряд (6.18) собственно расходящийся, то есть . Отсюда заключаем, что . Значит и ряд (6.19) также собственно расходящийся.

Наконец, пусть ряд (6.18) осциллирующий. Это означает, что не существует. Тогда заключаем, что не существует и предела . Отсюда делаем вывод, что ряд (6.19) осциллирующий. Теорема доказана.

Пример. Исследовать ряд

_. (6.23)

Этот ряд представляет собой геометрическую прогрессию и играет важную роль при изложении дальнейшей теории. Число x – знаменатель прогрессии может быть любым действительным числом .

При исследовании ряда (6.23) его предстоит рассмотреть при всех значениях x.

При x = –1, он принимает вид но этот ряд был уже рассмотрен нами в примере 3, §1, формула (6.9) и там установлено, что он осциллирующий.

При ряд (6.23) имеет вид

_. (6.24)

Здесь n-ый общий член ряда равен 1 и при он не стремиться к нулю, следовательно, не выполнен необходимый признак сходимости ряда, а потому ряд (6.24) расходится. Можно иначе, для ряда (6.24) усеченная сумма порядка n, имеет вид Отсюда , ряд (6.24) собственно расходящийся.

Далее будем считать, что . Составим усеченную сумму для ряда (6.23). Имеем . Применяя здесь, в правой части, формулу для нахождения суммы первых членов геометрической прогрессии, получим . Перепишем последнее равенство немного иначе

. (6.25)

Последовательность при выполнении условия является бесконечно малой последовательностью, дробь (x − фиксировано) есть ограниченная и постоянная величина. Значит правая часть (6.25) есть сумма постоянной и бесконечно малой, а потому существует предел и

.

Отсюда следует, что при ряд (6.23) сходится и имеет сумму равную . Другими словами, при справедливо равенство

.

Пусть, наконец . При этом условии, последовательность есть бесконечно большая. После этого из равенства (6.25) заключаем, что , то есть ряд (6.23) собственно расходящийся.

Полученные результаты можно записать так: ряд (6.23) сходится при и расходится при . Это же самое показано на числовой оси рис.67.

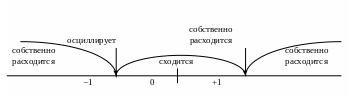
Рис. 67