2.2. Основные формулы и правила дифференцирования

Вычисление дифференциалов функций, также как и вычисление их производных, носит название дифференцирования. Так как дифференциал dy лишь множителем dх отличается от производной , то по таблице производных для элементарных функций (§1, п.1.12) легко составить таблицу дифференциалов для них:

1. , ; 2. ;

3. ; 4. ;

5. ; 6. ;

7. , ; 8. ;

9. ; 10. ;

11. ; 12. .

Правила дифференцирования (если речь идет о вычислении дифференциалов) выглядят так:

I. , где c = const, II. d (u ± v) = du ± dv,

III. d (u·v) = u·dv + v·du, IV. .

Все они легко получаются из соответствующих правил для производных (§1, п.1.4). Например,

.

2.3. Инвариантность формы дифференциала

В п.2.1 мы установили, что для случая, когда аргумент х является независимой переменной, дифференциал функции определяется формулой (3.16): dy = ·dх.

Покажем, что формула (3.16) является универсальной и справедлива не только в случае, когда аргумент х является независимой переменной, но и в случае, когда аргумент х сам является дифференцируемой функцией некоторой новой переменной t. Указанное свойство дифференциала функции обычно называют инвариантностью его формы.

Итак, пусть дана дифференцируемая в некоторой точке х функция y = f(x), аргумент х которой представляет собой дифференцируемую функцию x = (t) аргумента t. В таком случае мы можем рассматривать у как сложную функцию y = f((t)) аргумента t, а х – как промежуточный аргумент. В силу теоремы §1, п.1.6 производная y по t определяется формулой

(или . (3.18)

Поскольку переменную t мы можем рассматривать как независимую, производные функций x = (t) и y = f((t)) по аргументу t, согласно (3.17) равны .

Подставляя эти значения производных в формулу (3.18), придадим этой формуле вид

. (3.19)

Умножая обе части равенства (3.19) на dt, получим для dy выражение (3.16), т.е. вернемся к прежней форме дифференциала! Тем самым доказана инвариантность формы дифференциала функции, а именно: форма дифференциала может быть сохранена даже в том случае, если прежняя независимая переменная заменена новой.

Замечание. Возможность выражать производную через дифференциалы

, взятые по любой переменной, приводит к тому, что правила дифференцирования обратной функции и сложной функции становятся простыми алгебраическими тождествами

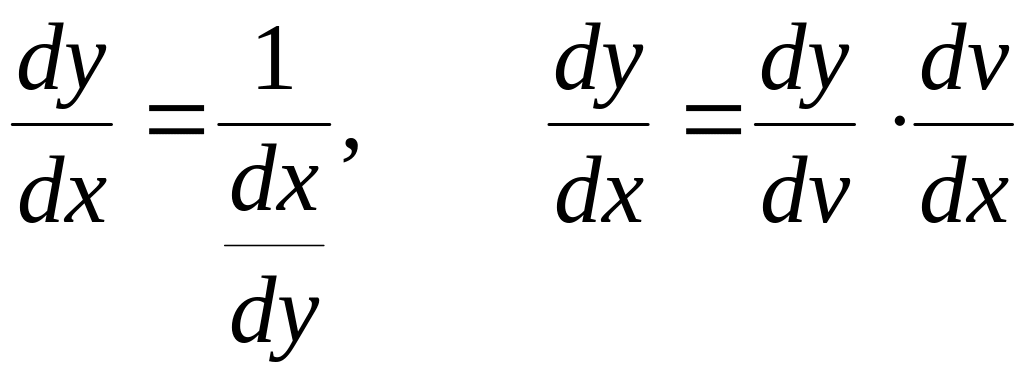(3.20)

(поскольку все дифференциалы здесь могут быть взяты по одной и той же переменной).

2.4. Использование дифференциала для приближенных вычислений

Перепишем формулу (3.13), заменив в ней главную часть приращения функции дифференциалом

. (3.21)

Из полученного выражения следует, что хотя дифференциал dy функции не равен приращению y этой функции, но, так как , то с точностью до бесконечно малой более высокого порядка, чем х, справедливо приближенное равенство

y  dy. (3.22)

Относительная погрешность этого равенства становится сколь угодно малой при достаточно малом х.

Выгода замены приращения функции у ее дифференциалом dy состоит в том, что dy зависит от х линейно, в то время как у представляет собой обыкновенно более сложную функцию от х.

Если положить х = х – х₀ и х₀ + х = х, то равенство (3.22) принимает вид: f (x) – f (x₀)  (x – x₀) или

f (x) = f (x₀) + (x – x₀). (3.23)

Формула (3.23) определяет способ приближенного вычисления функции. По этой формуле для значений х, близких к х₀, функция f(x) приближенно заменяется линейной функцией. Геометрически это соответствует замене участка кривой y = f(x), примыкающего к точке (х₀, f(x₀)), отрезком касательной к кривой в этой точке (см. формулу (3.3)).

В частности, взяв для простоты х₀ = 0 и ограничиваясь малыми значениями х, будем иметь приближенную формулу:

f (x)  f (0) + x. (3.24)

Отсюда, подставляя вместо f(x) различные элементарные функции, легко получить ряд приближенных формул:

(1+x)^  x; sin x  x; tg x x; e^x1+x; ln(1+x)  x и т.п.