1.6. Производная сложной функции
Теорема.
Пусть 1) функция v
x)
имеет в некоторой
точке x
производную
,
2) функция y
= f(v)
имеет в соответствующей точке v
производную
Тогда сложная функция у
= f(x))
в упомянутой точке х
также будет иметь производную, равную
произведению производных функций f(v)
и
x):
[ f(
x))
]'
=
или короче
(3.7)
Доказательство.
Придадим
х
произвольное приращение Δх;
пусть Δv
– соответствующее
приращение функции v
= (x)
и, наконец, Δу
– приращение функции
y = f(v),
вызванное
приращением Δv.
Воспользуемся соотношением (3.6), которое,
заменяя x
на v,
перепишем в виде
(
зависит от Δv
и вместе с ним стремится к нулю). Разделив
его почленно на x,
получим
.
Если x устремить к нулю, то, согласно (3.6) (при условии, что у = v), будет стремиться к нулю и Δv, а тогда, как мы знаем, будет также стремиться к нулю зависящая от Δv величина . Следовательно, существует предел
,
который и представляет собой искомую производную .
Таким образом, производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Случай сложной функции, полученной в результате нескольких суперпозиций, исчерпывается последовательным применением правила (3.7). Так, если у = f(u), u = (v), v = (x), то
. (3.8)
Примеры. 1. Пусть y = loga sin x, иначе говоря, y = loga v, где v = sin x. По правилу (3.7)
.
2.
,
т.е. y
= eu,
u = v2,
v = sin
x. По
правилу (3.8)
.
1.7. Производная показательно – степенной функции
Пусть u = u(x) > 0 и v = v(x) – функции, имеющие производные в фиксированной точке x. Найдем производную функции y = uv. Логарифмируя это равенство, получим: ln y = v ln u.
Продифференцируем обе части данного равенства по x:
.
Отсюда
,
или
. (3.9)
Таким образом, производная показательно – степенной функции состоит из двух слагаемых: первое слагаемое получается, если при дифференцировании предположить, что и есть функция от х, а v есть постоянная (т.е. рассматривать uv как степенную функцию); второе слагаемое получается, если предположить, что v есть функция от х, а u = const (т.е. рассматривать uv как показательную функцию).
Примеры. 1. Если y = xtg x, то, полагая u = x, v = tg x, согласно (3.9) имеем
= tg x xtg x – 1 + xtg x ln x sec2x.
Прием, примененный в данном случае для нахождения производной и состоящий в том, что сначала находят производную логарифма рассматриваемой функции, широко применяется при дифференцировании функций: при отыскании производной функции эти функции сначала логарифмируют, а затем из равенства, полученного после дифференцирования логарифма функции, определяют производную функции. Такая операция называется логарифмическим дифференцированием.
2. Требуется найти производную от функции
.
Логарифмируя, находим:
ln
y = 2
ln
(x
+ 1)
+
ln
(x
–
1) – 3 ln
(x
+ 4)
– x.
Дифференцируем обе части последнего равенства:
.
Умножая
на у
и подставляя
вместо у,
получаем:
.
1.8. Производная неявно заданной функции
Неявная форма записи функциональной зависимости имеет вид
F(x, y) = 0.
Чтобы найти производную неявной функции y = y(x), нужно взять производную от обеих частей равенства F(x, y) = 0, считая у функцией от х, и полученное уравнение разрешить относительно .
Допустим, что функция задана уравнением
.
Если здесь у есть функция от х, определяемая этим равенством, то это равенство есть тождество.
Дифференцируя обе части этого тождества по х, считая, что у есть функция от х, получим:
откуда
.
Из приведенного примера следует, что для нахождения значения производной неявной функции при данном значении аргумента х нужно знать и значение функции у при данном значении х.
Рассмотрим
еще один пример. Опредилим уравнения
касательной и нормали к кривой второго
порядка, заданной уравнением
(гипербола) в точке М0
(x0,
y0).
Уравнение
прямой с угловым коэффициентом k,
проходящий через точку М0
(x0,
y0)
имеет вид (см.
книга 3, гл.2, §7)
.
Для касательной (см. §1, п.1.1.)
,
поэтому уравнение касательной имеет
вид
(
).
Наряду с касательной к кривой в данной точке очень часто приходится рассматривать нормаль.
Определение. Нормалью к кривой в данной точке называется прямая, проходящая через данную точку, перпендикулярную к касательной в этой точке.
Из определения нормали следует, что ее угловой коэффициент kn связан с угловым коэффициентом kt касательной равенством (см. книга 3, гл.2, §11)
,
т.е.
.
Следовательно, уравнение нормали к кривой в точке М0(x0,y(x0)) имеет вид
.
Теперь из уравнения гиперболы, рассматривая
его как уравнение, неявно задающее
функцию y
и x,
находим
в точке x0,
т.е.
.
Для этого сначала дифференцируем
уравнение гиперболы, считая y
функций от x,
затем выражаем
и
подставляем значение x
= x0:
.
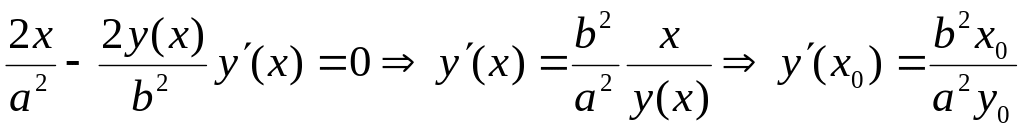Итак, окончательно имеем
– уравнение касательной.
– уравнение нормали.