1.4. Простейшие правила вычисления производных

Теперь укажем ряд простых правил, с помощью которых станет возможным вычисление производной для любой функции составленной из элементарных при посредстве конечного числа арифметических действий и суперпозиций.

Теорема 1. Постоянный множитель можно выносить за знак производной, т.е. если у = с f(x), где с = const, то у' = с f'(x).

Доказательство. Если независимая переменная х получит приращение , то новое значение функции у будет у + = с f(x+ ).

Отсюда и окончательно

Теорема 2. Производная суммы конечного числа функций, имеющих (в определенной точке) производную, равна соответствующей сумме производных этих функций (в той же точке).

Для случая, например, двух слагаемых, имеем:

y = u(x) + v(x), .

Заметим, что выражение y = u(x) – v(x) равносильно y = u(x) + (–1)v(x) и .

Доказательство. Придадим x приращение ∆x; тогда u, v и y получают приращения соответственно ∆u, ∆v и ∆y. Их новые значения u+∆u, v+∆v и y+∆y связаны тем же соотношением:

y + ∆y= (u+∆u) + (v+∆v).

Отсюда

∆y = ∆u + ∆v, и ,

так что .

Этот результат легко может быть распространен на любое число слагаемых (и притом, тем же методом).

Теорема 3. Производная произведения двух непрерывных функций, имеющих производную, равна произведению производной первой функции на вторую функцию плюс произведение первой функции на производную второй функции, т.е. если y = u(x)·v(x), то .

Доказательство. Приращению отвечают, как и выше, приращения ∆u, ∆v и ∆y; при этом

y + ∆y = (u+∆u)·(v+∆v), так что

∆y = ∆u·v + u·∆v + ∆u·∆v и

.

Так как при ∆x  , в силу непрерывности v(x) и ∆v  , то

.

На основании доказанной теоремы легко получается правило дифференцирования произведения любого числа функций.

Так, если имеем произведение трех функций , то, представляя правую часть как произведение u и , получим:

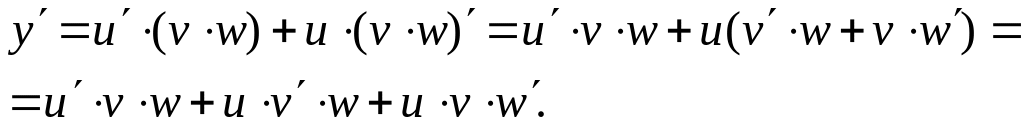
Таким приемом можем получить аналогичную формулу для произведения любого (конечного) числа функций. Именно, если y = u₁, u₂, .., u_n, то

.

Теорема 4. Производная дроби (т.е. частного от деления двух непрерывных функций) равна дроби, у которой знаменатель есть квадрат знаменателя данной дроби, а числитель есть разность между произведением знаменателя на производную числителя и произведением числителя на производную знаменателя, т.е. если (где ), то

Доказательство. При тех же обозначениях, что и выше, имеем

так что

и

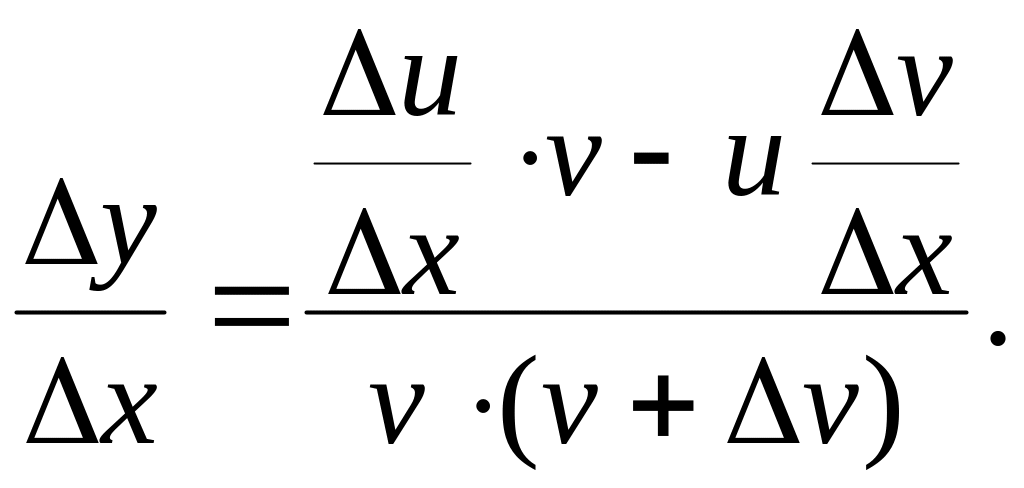
Устремляя здесь к нулю (причем одновременно и ) убеждаемся, что

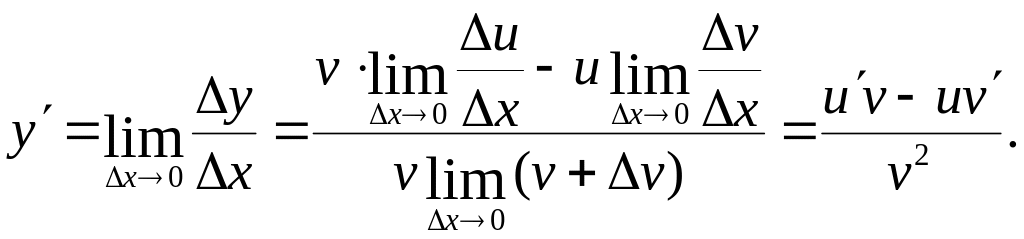
1.5. Теорема о непрерывности функции, имеющей производную

Теорема. Если функция в некоторой точке x = x₀ имеет (конечную) производную , то

1. приращение функции может быть представлено в виде

, (3.6)

или, короче, , где  есть величина, зависящая от x и вместе с ним стремящаяся к нулю, т.е. ;

2. функция в этой точке необходимо непрерывна.

Доказательство. 1) Согласно определению производной, . Пользуясь теоремой, о представлении функции имеющей предел в виде суммы этого предела и бесконечно малой, запишем

, где .

Определяя отсюда y, придем к формуле (3.6).

2) Чтобы доказать непрерывность функции, рассмотрим выражение (3.6). При x   сумма в правой части (3.6) обращается в нуль. Следовательно, , или , а это означает, что функция в точке x₀ непрерывна.

Из доказанной теоремы следует, что функция, имеющая производную в данной точке, будет непрерывной в этой точке. Однако непрерывная в данной точке функция не всегда имеет производную в этой точке. Так, в точке x₀ = 1 функция y = |x – 1| является непрерывной, но производной в этой точке не имеет. Это означает, что данное условие является лишь необходимым.