5.5.3. Наибольшее и наименьшее значение функции на отрезке

Пусть функция непрерывна на отрезке [a,b]. Тогда на этом отрезке функция достигает наибольшего и наименьшего значений (2-ая теорема Вейерштрасса). Остановимся для определенности на наибольшем значении.

Если оно достигается в некоторой точке между a и b, то это одновременно будет одним из максимумов (очевидно, наибольшим); но наибольшее значение может достигается и на одном из концов промежутка, a или b.

Итак, функция на отрезке [a,b] достигает своего наибольшего значения либо на одном из концов этого отрезка, либо в такой внутренней точке этого отрезка, которая является точкой максимума.

То же самое можно сказать и о наименьшем значении функции: оно достигается либо на одном из концов данного отрезка, либо в такой внутренней точке, которая является точкой минимума.

Из предыдущего вытекает следующее правило: если требуется найти наибольшее значение непрерывной функции на промежутке [a,b], то надо:

1) найти все максимумы функции на отрезке;

2) определить значения функции f(a) и f(b) на концах отрезка;

3) из всех полученных выше значений функции выбрать наибольшее; оно и будет представлять собой наибольшее значение функции на отрезке.

Аналогичным образом следует поступать и при определении наименьшего значения функции на отрезке.

С помощью теории максимума и минимума решаются многие задачи геометрии, физики и т.д. Рассмотрим некоторые из таких задач.

Задача 1. Затраты на перевозку груза по железной дороге в единицу времени состоят из двух частей: постоянной, равной a, и переменной, пропорциональной v³, где v – скорость. При какой скорости затраты на перевозку груза будут наименьшими?

Решение. Обозначим расходы на перевозку груза в единицу времени через q. Тогда q = a + bv³, где b – коэффициент пропорциональности.

Затраты на перевозку грузу составляют

,

где S – расстояние, на которое перевозится груз.

Затраты на перевозку необходимо выбрать наименьшими. Для этого нужно исследовать функцию

на минимум. Находим

, ,

откуда

, , так как b > 0 и S > 0.

При этой скорости движения затраты будут наименьшими так как при v → 0 и v → ∞ затраты неограниченно возрастают.

Задача 2. Дальность S полета снаряда, выпущенного с начальной скоростью v₀ из орудия, наклоненного под углом φ к горизонту, определяется формулой

,

где g – ускорение свободного падения. Определить угол φ₀, при котором дальность S будет наибольшей при данной начальной скорости v₀.

Решение. Величина S представляет собой функцию переменного угла φ. Исследуем эту функцию на максимум на отрезке 0  φ  :

,

откуда

,

следовательно, при значении φ = дальность полета S имеет максимум

.

Значения функции S(φ) на концах отрезка [0, ] равны:

S(0) = 0, S( ) = 0.

Таким образом, найденный максимум и есть искомое наибольшее значение S.

5.5.4. Асимптоты

Очень часто приходится исследовать форму кривой y = f(x), а значит, и характер изменения соответствующей функции при неограниченном возрастании (по абсолютной величине) абсциссы x или ординаты y переменной точки М(x,y) кривой или абсциссы и ординаты одновременно. При этом важным частным случаем является тот, когда исследуемая кривая при удалении ее переменной точки М(x,y) в бесконечность (расстояние этой точки от начала координат неограниченно возрастает) неограниченно приближается к некоторой прямой.

Определение. Если рассеяние δ от точки кривой до некоторой определенной прямой по мере удаления точки в бесконечность стремится к нулю, то эта прямая называется асимптотой кривой (рис.26).

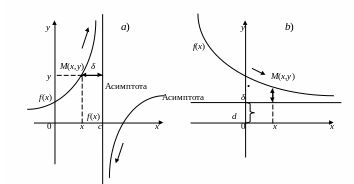
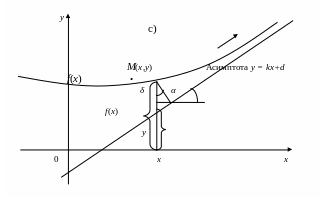
Рис. 26

Кривые с бесконечной ветвью могут иметь три вида асимптот: вертикальные (т.е. параллельные оси ординат, рис.26,а), горизонтальные (т.е. параллельные оси абсцисс, рис.26,b) и наклонные (рис.26,с).