5.5.2. Максимумы и минимумы функции.

Определение. Говорят, что функция f(x) имеет в точке x₀ максимум (или минимум), если эту точку можно окружить такой окрестностью (x₀ – δ, x₀ + δ), содержащейся в промежутке [a,b], где задана функция, что для всех ее точек x выполняется неравенство f(x) < f(x₀) (или f(x) > f(x₀)).

Иными словами, точка x₀ доставляет функции f(x) максимум (минимум), если значение f(x₀) оказывается наибольшим (наименьшим) из значений, принимаемых функцией в некоторой (хотя бы малой) окрестности этой точки. Отметим, что самое определение максимума (минимума) предполагает, что функция задана по обе стороны от точки x₀.

Если функция имеет максимумы в точках x₀ и x₁, то, применяя к промежутку [x₀,x₁] 2-ю теорему Вейерштрасса (гл.1, §12, п.12.9) видим, что наименьшего своего значения в этом промежутке функция достигает в некоторой точке x₂ между x₀ и x₁ и имеет там минимум. Аналогично, между двумя минимумами непременно найдется максимум. В случае, когда функция имеет конечное число максимумов и минимумов, они попросту чередуются.

Максимумы и минимумы функции называются экстремумами или экстремальными значениями функции.

Укажем метод нахождения экстремальных значений.

Теорема 1 (необходимое условие существования экстремума). Если дифференцируемая функция f(x) имеет в точке x = x₀ максимум или минимум, то ее производная в этой точке обращается в нуль, т.е. = 0.

Доказательство этой теоремы достигается применением к промежутку (x₀  – δ, x₀ + δ), о котором была речь выше, теоремы Ферма (§4, п.4.2).

Из теоремы 1 непосредственно вытекает следствие: если при всех рассматриваемых значениях аргумента x функция f(x) имеет производную, то она может иметь экстремум (максимум или минимум) только при тех значениях, при которых производная обращается в нуль (касательная параллельна оси Oх, рис.18, точки x = ξ₁ и x = ξ₂ и рис.25, точки x = x₁ и x = x₂). Обратное заключение неверно: не при всяком значении, при котором производная обращается в нуль, обязательно существует максимум или минимум. Так, на рис.25 изображена функция, у которой при x = x₃ производная обращается в нуль (касательная горизонтальна), но в этой точке функция не имеет, ни максимума, ни минимума, а налицо перегиб, так как касательная пересекает кривую.

Точки, в которых производная существует и равна нулю, называются стационарными.

Если расширить класс рассматриваемых функций f(x) и допустить, что в отдельных точках производная равна бесконечности или вовсе не существует, то не исключена возможность того, что экстремум придется на какую-либо из таких точек. Например, функция, изображенная на рис.25, очевидно, имеет максимум при x = x₅, в то время как производная ее в этой точке равна ∞; точно также в точке x = 0 имеет максимум функция у = –|x|, хотя производной для нее в этой точке не существует. Следовательно, и точки, в которых производная бесконечна или не существует, также могут доставлять функции экстремум. Но, разумеется, и в этом случае также – одно лишь отсутствие производной или обращение ее в бесконечность не гарантирует наличия экстремума. Примерами могут служить функции и (с дополнительным условием y = 0 при x = 0). Первая из них имеет бесконечную производную в точке x = 0 (см. также рис.16,б, кривые (1) и (2)), вторая же вовсе не имеет производной в этой точке, но точка x = 0 не доставляет экстремума ни той, ни другой функции (ибо в любой ее окрестности обе функции принимают и положительные и отрицательные значения).

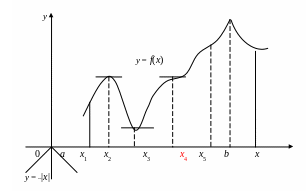
Рис. 25

Таким образом, функция может иметь экстремум лишь в трех случаях: либо в тех точках, где производная существует и равна нулю, либо бесконечности; либо в тех точках, где производной не существует.

Значения аргумента, при которых производная обращается либо в нуль, либо в бесконечность, либо вовсе не существует, называются критическими точками или критическими значениями.

Из предыдущего следует, что не при всяком критическом значении функция имеет максимум или минимум. Однако, если в какой – либо точке функция достигает максимума или минимума, то эта точка наверняка является критической. Поэтому для разыскания экстремума функции поступают следующим образом: находят все критические точки, а затем, исследуя отдельно каждую критическую точку, выясняют, будет ли в этой точке максимум или минимум функции или же не будет ни максимума, ни минимума.

Исследование функции в критических точках опирается не следующие теоремы.

Теорема 2 (достаточные условия существования экстремума). Пусть функция f(x) непрерывна в некоторой окрестности (x₀  – δ, x₀ + δ), точки x₀. Если во всех точках этого интервала (по крайней мере, для x = x₀) существует конечная производная и как слева от x₀, так и справа от x₀ (в отдельности) сохраняет определенный знак. Тогда возможны следующие три случая:

I. > 0 при x < x₀ и < 0 при x > x₀, т.е. производная при переходе через точку x₀ меняет знак плюс на минус. В этом случае, в промежутке (x₀ – δ, x₀), функция f(x) возрастает, а в промежутке (x₀, x₀ + δ), убывает, так что значение f(x₀) будет наибольшим в промежутке (x₀ – δ, x₀+ δ), т.е. в точке x₀ функция имеет максимум (рис.25, x₀ = x₁).

II. < 0 при x < x₀ и > 0 при x > x₀, т.е. производная при переходе через точку x₀ меняет знак минус на плюс. В этом случае аналогично убеждаемся, что в точке x₀ функция имеет минимум (рис.25, x₀ = x₂).

III. > 0 как при x < x₀, так и при x > x₀, либо же < 0 и слева и справа от x₀, т.е. при переходе через x₀, не меняет знака. Тогда функция либо все время возрастает, либо все время убывает; в любой близости от x₀ с одной стороны найдутся точки x, в которых f(x) < f(x₀), а с другой – точки x, в которых f(x) > f(x₀), так что в точке x₀ никакого экстремума нет (например, рис.25, x₀ = x₃ – точка перегиба).

Итак, мы получаем первое правило для исследования критической точки на экстремум: подставляя в производную сначала x < x₀, а затем x > x₀, устанавливаем знак производной поблизости от точки x₀ слева и справа от нее; если при этом производная меняет знак плюс на минус, то налицо максимум, если меняет знак минус на плюс, то – минимум; если же знака не меняет, то экстремума вовсе нет.

В тех случаях, когда критическая точка x₀ – стационарная, т.е. = 0 и в некоторой окрестности точки x₀ существует непрерывная вторая производная тогда при разыскании экстремумов исследование знака первой производной вблизи испытуемой точки можно заменить исследованием знака второй производной в самой этой точке; покажем это.

Итак, пусть функция f(x) не только имеет производную в окрестности точки x₀, но и вторую производную непрерывную в некоторой окрестности точки x₀. Точка x₀ – стационарная, т.е. = 0. Если > 0, то, по теореме о сохранении знака непрерывной функции (гл.1, §12, п.12.9, теорема 1) и условия монотонности функции (гл.3, §4, п.4.2.2, теорема 2) – функция в окрестности точки x = x₀ возрастает, т.е. вблизи точки x₀ слева <  = 0, а справа >  = 0. Таким образом, производная меняет знак минус на плюс и, следовательно, f(x) имеет в точке x = x₀ минимум. Если < 0, то в точке x = x₀ убывает, меняя знак плюс на минус, так, что налицо максимум.

Таким образом, можно сформулировать второе правило для исследования стационарной точки x₀ на экстремум: подставляем x₀ во вторую производную ; если > 0, то функция имеет минимум, если же < 0, то – максимум.

Второе правило ничего не дает, когда вторая производная в точке x₀ обращается в нуль. В этом случае решение вопроса зависит от поведения высших производных. Если , то из теоремы 1, гл.1, §12, п.12.9 и теоремы 3, гл.3, §7, п.7.1 следует, что точка x₀ есть точка перегиба. Если же , а , то в точке x = x₀ имеет место экстремум: при – минимум, а при – максимум.

Для большей общности предположим теперь, что не только , но и все производные до (n – 1) – го порядка включительно от функции f(x) обращаются в нуль при x = x₀: = = . . . = = 0,

между тем как .

Тогда справедливо следующее третье правило: если первая из производных, не обращающихся в точке x₀ в нуль, есть производная нечетного порядка (n =2m – 1, m N), функция не имеет в точке x₀ ни максимума, ни минимума (при m  2, в точке x = x₀ имеет место перегиб). Если такой производной является производная четного порядка (n = 2m, m N), функция в точке x₀ имеет максимум или минимум, смотря по тому, будет ли эта производная отрицательна или положительна.

Поставим теперь вопрос о разыскании наибольшего и наименьшего из всех значений, которые непрерывная функция f(x) принимает на промежутке [a,b]; по 2-ой теореме Вейерштрасса (гл.1, §12, п.12.9), такие наибольшие и наименьшие значения существуют.