5.4.2. Аппроксимация функций
В этом разделе наряду с формулой Тейлора будет изложен еще один способ приближенного изображения (аппроксимации) функции с помощью полинома.
Пусть функция у = f(x) заданна на промежутке [a,b]. Выделим здесь произвольно п интерполяционных узлов x1, x2,…, xn.
Построим интерполяционный полином Лагранжа степени не выше n – 1, который бы в этих узлах приобретал те же значения, что и функция f(х), т.е.
. (3.62)
Интерполяционный полином Лагранжа определяется равенством (3.61)
=
=
. (3.63)
Свойства полинома Лагранжа , выраженные равенствами (3.62), геометрически означают, что график полинома Лагранжа у = (рис.22, пунктирная кривая) имеет в интерполяционных узлах x1, x2,…, xn такие же ординаты, что и график функции y = f(x) (рис.22, сплошная кривая).
Поскольку
полином Лагранжа
принимают
за приближенное выражение для f(x),
возникает
потребность найти ошибку
приближенного равенства
.
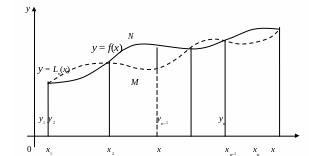
Рис. 22
Геометрическое
значение
такое же,
как и для остаточного члена формулы
Тейлора:
есть отрезок
ординаты МN,
расположенный
между графиками функции f(х)
и полинома
в точке х,
взятой со
знаком плюс, если график f(х)
в точке х
проходит выше графика
(рис.22), и со
знаком минус, если ниже.
Теорема.
Пусть
на промежутке [a,b]
для функции f(x)
существуют
последовательные производные
и пусть интерполяционные узлы
лежат в промежутке [a,b].
Тогда
можно найти, по крайней мере, одну такую
точку х
= ξ,
которая лежит в промежутке [a,b],
что выполняется
равенство
(3.64)
для всех х, которые лежат в промежутке [a,b].
Доказательство. Пусть точка х зафиксирована на промежутке [a,b] и не совпадает ни с одним из интерполяционных узлов. Рассмотрим вспомогательную функцию
.
(3.65)
При
этих условиях вспомогательная функция
Н(z)
имеет на
[a,b]
(n
+ 1)
корней и будет обращаться в нуль на
концах каждого из отрезков
,
. (3.66)
Применяя
теорему Роля к каждому из этих отрезков
убеждаемся, что производная
,
имеет не менее п
корней в п
разных точках
,
расположенных
внутри отрезков
,
таких
что
.
Применив
теорему Ролля к производной
,
мы убеждаемся, что производная
имеет п
– 1
корней на [a,b].
Продолжая эти рассуждения, придем к
заключению, что на рассматриваемом
отрезке [a,b]
производная
имеет хотя бы один корень, который
обозначим через
,
т.е.
. (3.67)
Найдем
из (3.65)
.
Учитывая, что
–
полином степени
п,
а тогда, как
установлено ранее,
,
имеем
. (3.68)
Далее,
степень полинома
не выше п
– 1, и потому
.
Следовательно
.
Отсюда находим
. (3.69)
Причем, ξ не совпадает с узлами x1, x2,…, xn и точкой х. Теорема доказана.
Равенство (3.69) называется интерполяционной формулой Лагранжа с остаточным членом. Остаточный член Rn(x) в этой формуле определяется равенством
.
Отсюда,
если известна верхняя граница
,
получим оценку для абсолютной погрешности вычисления значений функции f(х) с использованием интерполяционной формулы Лагранжа
.
Из полученной оценки следует, что чем больше используется интерполяционных узлов, тем выше точность вычисления.
Пример. Функцию
(3.70)
аппроксимировать
с помощью интерполяционного полинома
Лагранжа
,
который, в пяти узлах
приобретал бы те же значения, что и
заданная функция (3.70), и оценить точность
этого приближения.
Прежде всего, вычислим значения этой функции в интерполяционных узлах. Из (3.70) находим
Следовательно,
полином
должен быть построен по таблице
-
x
–2
–1
0
1
2
y
0
–1
0
1
0
Поэтому
.
Для
и
имеем
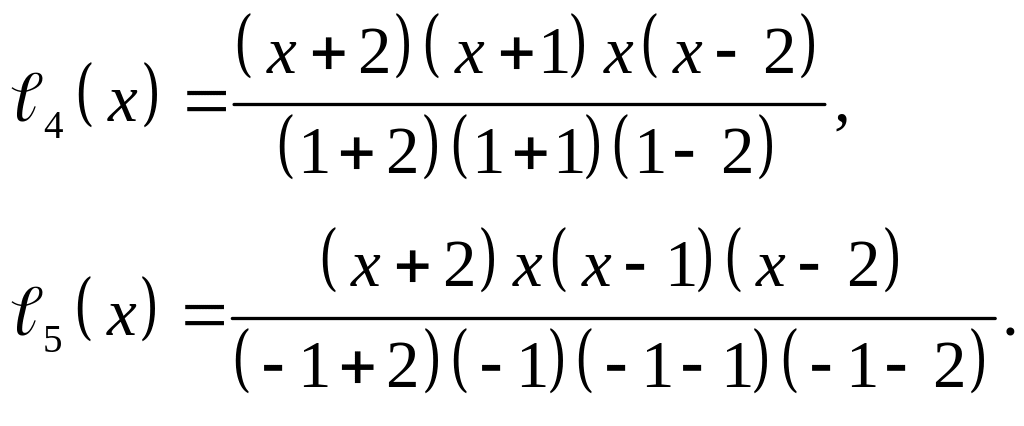
Таким образом,
и
после упрощений получаем
.
Далее,
для остаточного члена R5(x)
нужно
вычислить
.
.
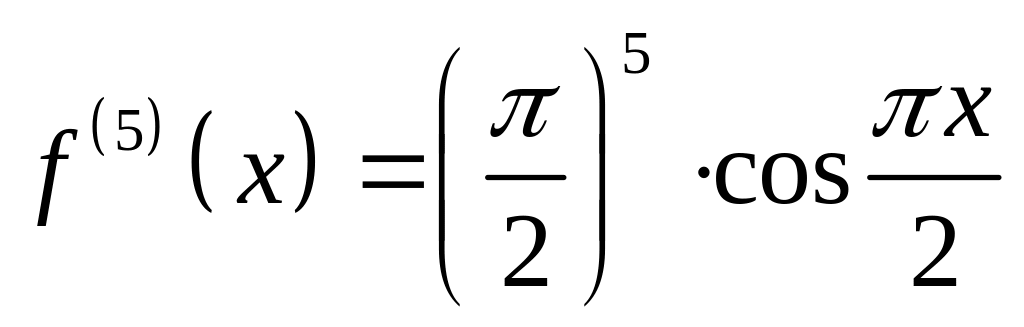Поэтому для функции этого примера имеет место такая формула интерполяции Лагранжа с остаточным членом
.
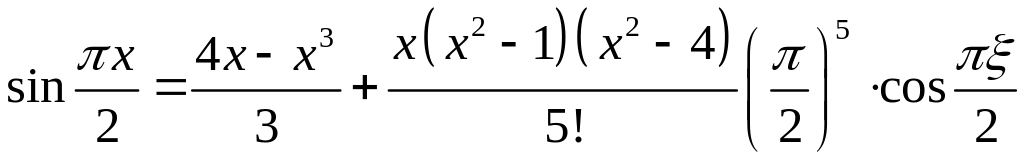Если
для вычисления значений функции
пользоваться приближенной формулой
,
то абсолютная погрешность такого
вычисления, учитывая, что |
|
≤ 1 составит
.
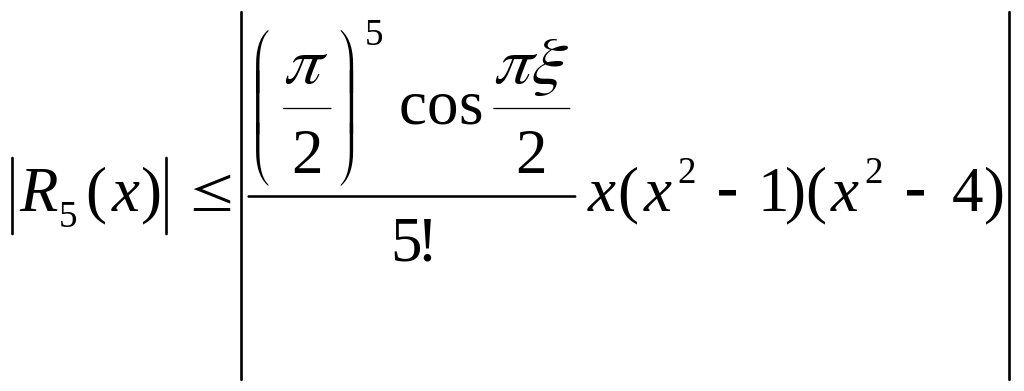
Так,
для
абсолютная погрешность вычисления
составит
0,11.
На
рис.23 изображены графики функции
(сплошная кривая) и интерполяционного
полинома
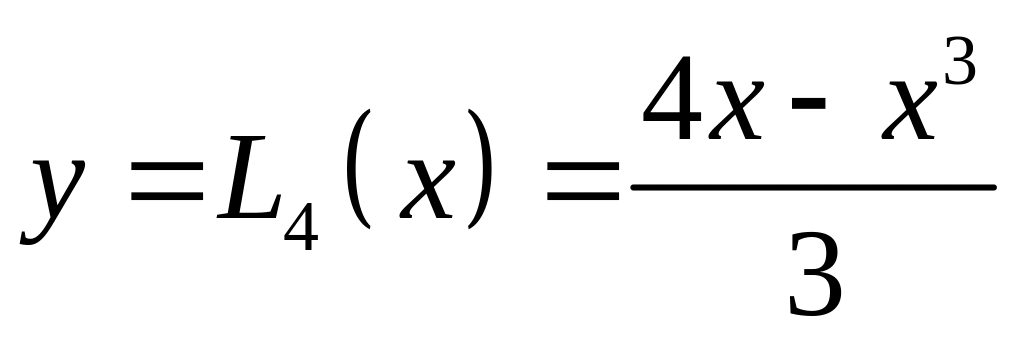(пунктирная кривая).
Рис. 23
Отметим,
что
и абсолютная погрешность аппроксимации
составляет 0,08.
Для достижения более высокой точности вычисления необходимо
увеличивать число интерполяционных узлов.