Рассмотрим теперь вспомогательную функцию

.

Эта функция удовлетворяет всем условиям теоремы Ролля. В самом деле, F(x) непрерывна в [a,b], так как непрерывны g(x) и f(x); производная существует в (а,b), именно, она равна

.

Наконец, прямой подстановкой убеждаемся, что . Вследствие этого в промежутке (а,b) существует такая точка , что . Иначе говоря,

или

.

Разделив на (это возможно, так как ), получаем требуемое равенство (3.36). Теорема доказана.

Ясно, что теорема Лагранжа является частным случаем теоремы Коши. Для получения формулы конечных приращений (3.31) из формулы Коши следует положить g(x) = x. Теорему Коши называют обобщенной теоремой о среднем значении (в дифференциальном исчислении).

Замечание. В формуле (3.36) вовсе необязательно считать, что b > a.

§5. Применения дифференциального исчисления

5.1. Раскрытие неопределенностей (правило Лопиталя)

Применим теперь понятие производной и доказанные в предыдущем параграфе теоремы для раскрытия неопределенностей. Последующие теоремы настоящего параграфа принадлежат, в основном, Лопиталю и Бернулли. Высказанное в них правило обычно называют правилом Лопиталя.

5.1.1. Раскрытие неопределенности вида

Теорема 1. Если функции f(x) и g(x) удовлетворяют условиям:

1) функции определены и имеют конечные производные и причем  0, в некоторой окрестности точки х₀, за исключением быть может, самой точки х₀;

2) , ;

3. существует (конечный или нет) предел ,

тогда существует и предельное значение определяемое формулой

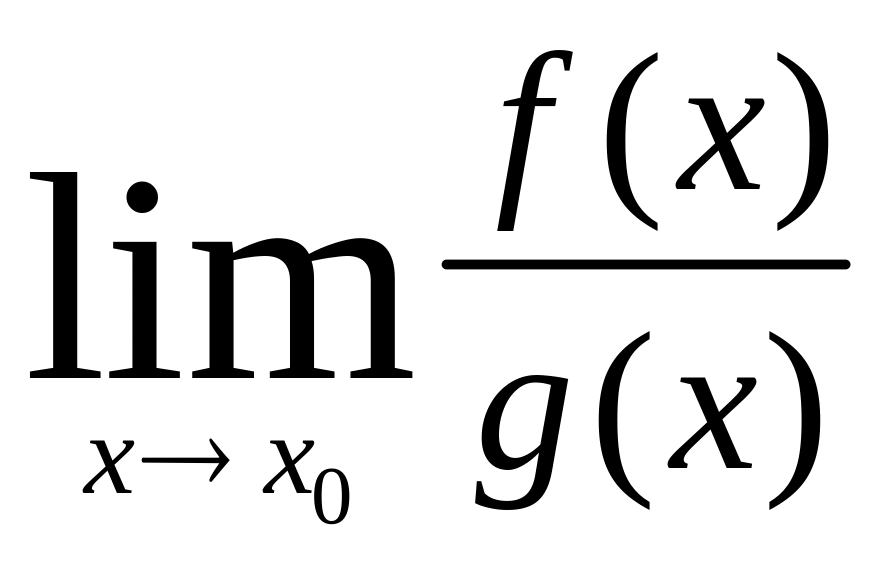= . (3.37)

Доказательство. Доопределим функции f(x) и g(x) в точке х₀, положив их равными нулю в этой точке. Тогда эти функции окажутся непрерывными во всем замкнутом промежутке ; их значения в точке х₀ совпадают с пределами при х  х₀ ввиду 2), а в прочих точках непрерывность вытекает из существования конечных производных см. 3). Здесь – произвольная точка, принадлежащая окрестности точки х₀, указанной в формулировке теоремы. Кроме того, отлична от нуля всюду внутри этого сегмента. Таким образом, для f(x) и g(x) на сегменте выполнены все условия теоремы Коши (§4, п.4.3). Согласно этой теореме, внутри сегмента найдется точка такая, что

,

где . Но, по условию, f(x₀) = g(x₀) = 0, значит

.

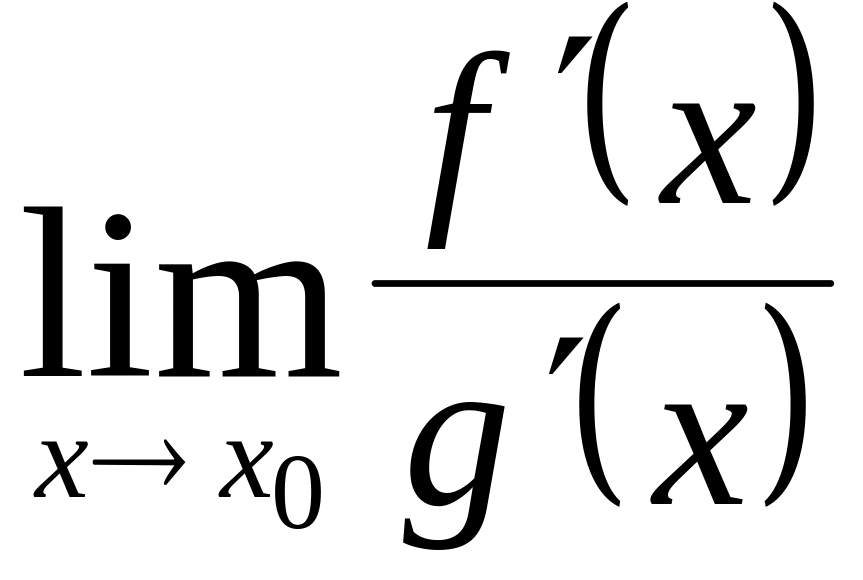Если , то и также стремится к х₀, так как заключено между х₀ и . По условию теоремы существует . Следовательно, этот предел будет таким же и для , и для , т.е.

.

Отсюда ясно, что

,

и, окончательно,

= .

Таким образом, доказанная теорема дает нам правило для раскрытия неопределенности вида , сводящее вычисление предельного значения отношения двух функций к вычислению предельного значения отношения их производных, если последнее существует. Отметим, что предел отношения производных может не существовать, тогда, как предел отношения функций существует. Например, можно взять х₀ = 0,

Тогда:

,

как произведение бесконечно малой на ограниченную функцию;

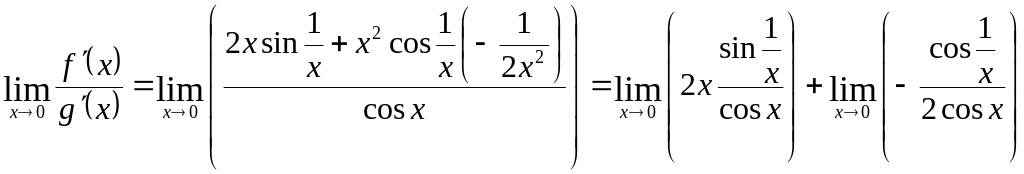– для второго слагаемого предела не существует. Следовательно, правило Лопиталя "действует" не всегда.

Замечания. 1) Если к условиям теоремы 1 добавить требование непрерывности производных и в точке х₀, то, при условии, что   0 формула (3.37) может быть переписана в виде:

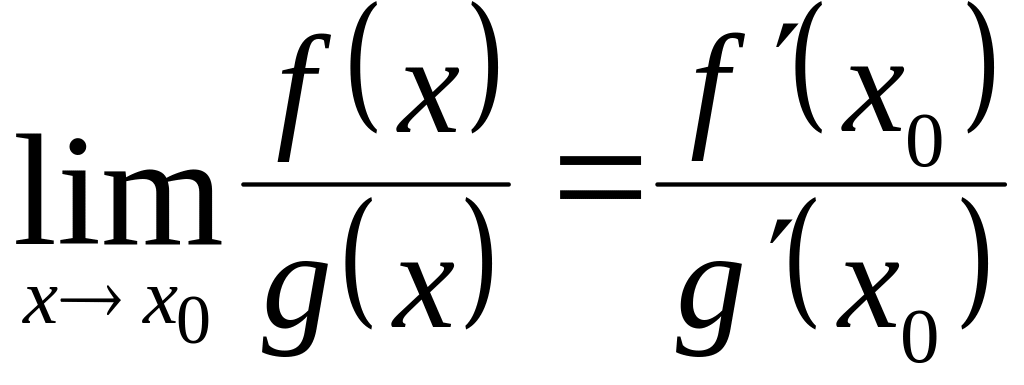(3.38)

2) Если производные и удовлетворяют тем же требованиям, что и сами функции f(x) и g(х), то правило Лопиталя можно применять повторно (т.е. предельное значение отношения первых производных функций f(x) и g(х) можно заменять предельным значением отношения вторых производных этих функций). При этом получим:

и т.д.

Теорема 1 легко переносится на случай, когда аргумент х стремится не к конечному, а к бесконечному пределу х₀ = +  или х₀ = – . Ограничимся тем, что сформулируем теорему для случая, когда х₀ = + .

Теорема 2. Пусть: 1) функции f(x) и g(х) определены в промежутке а,+), 2) , 3) существуют в промежутке а,+) конечные производные и , причем  0, и, наконец, 4) существует (конечный или нет) предел

.

Тогда и

(3.39)

Примеры: 1) Найти предел: . Для вычисления предела применим правило Лопиталя.

.

2) Найти предел: .

Отношение производных последовательно упрощается:

;

при х  0 оно, очевидно, стремится к 2. Таков же будет, согласно теореме, и искомый предел.

Обратим внимание на то, что здесь отношение производных снова представило неопределенность вида , но раскрыть эту определенность оказалось возможным не повторным применением правила Лопиталя, а путем элементарных преобразований. Важно подчеркнуть, что при этом допустимы всякие упрощения получаемых выражений, сокращение общих множителей, использование уже известных пределов и т.п.

3) Следующий предел вычисляется трехкратным применением правила Лопиталя:

.