4.2.1. Условие постоянства функции

Теорема. Если функция f(x) дифференцируема на интервале (a,b) и если всюду на этом интервале , то функция f(x) является постоянной на интервале (a,b).

Доказательство. Пусть х₀ – некоторая фиксированная точка интервала (a,b), а х – любая точка этого интервала.

Сегмент [х₀,х] целиком принадлежит интервалу (a,b). Поэтому функция f(x) дифференцируема (а стало быть и непрерывна) всюду на сегменте [х₀,х]. Это дает право применить к функции f(x) на сегменте [х₀,х] теорему Лагранжа. Согласно этой теореме внутри сегмента [х₀,х] найдется точка ξ такая, что

. (3.35)

По условию производная функции f(x), равна нулю всюду в интервале (a,b). Стало быть, и из формулы (3.35) получаем . Это и означает, что функция f(x) постоянна всюду на интервале (a,b).

Данное утверждение имеет простой геометрический смысл: если касательная в каждой точке некоторого участка кривой у = f(x) параллельна оси Ох, то указанный участок кривой у = f(x) представляет собой отрезок прямой, параллельный оси Ох.

4.2.2. Условие монотонности функции

Теорема 1. Для того чтобы дифференцированная на интервале (a,b) функция f(x) не убывала (не возрастала) на этом интервале, необходимо и достаточно, чтобы производная этой функции была неотрицательной (неположительной) всюду на этом интервале.

Доказательство. Достаточность. Пусть всюду на интервале (a,b). Требуется доказать, что f(x) не убывает (не возрастает) на интервале (a,b). Пусть х₁ и х₂ – любые две точки интервала (a,b), удовлетворяющие условию х₁ < х₂. Функция f(x) дифференцируема (а стало быть и непрерывна) всюду на сегменте [х₁,х₂]. Поэтому к f(x) можно применить на сегменте [х₁,х₂] теорему Лагранжа, в результате чего получим

f(x₂) – f (x₁) = (х₂ – х₁) f'(ξ), где х₁ < ξ < х₂.

Отсюда (так как по условию f '(ξ) ≥ 0 (≤ 0), (х₂ – х₁) > 0) получаем

f(x₂)  f(x₁) (f(x₂) ≤ f(x₁)), что и доказывает неубывание (невозрастание) f(x) на интервале (a,b).

Необходимость. Пусть функция f(x) дифференцируема на интервале (a,b) и не убывает (не возрастает) на этом интервале. Требуется доказать, что (≤ 0) всюду на этом интервале. Придадим аргументу х приращение Δх и рассмотрим отношение .

Так как f(x) функция неубывающая, то

f(x + Δх)  f(x) при Δх > 0 и f(x + Δх) ≤ f(x) при Δх < 0.

В обоих случаях

,

а, следовательно,

,

что и требовалось доказать.

В рассмотренном случае для монотонной функции f(x) не была исключена возможность сохранять в некоторых промежутках и постоянные значения, а для ее производной – обращаться в этих промежутках тождественно в нуль. Если мы эту возможность исключим, то придем к случаю монотонного возрастания (или убывания) в строгом смысле.

Теорема 2. Для того, чтобы функция f(x) возрастала (убывала) на интервале (а,b), достаточно, чтобы производная была положительной (отрицательной) всюду на этом интервале.

Доказательство проводится по той же схеме, что и доказательство достаточности в предыдущей теореме 1. Пусть х₁ и х₂ – любые две точки интервала (а,b), удовлетворяющие условию х₁ < х₂. Записывая для сегмента [х₁,х₂] формулу Лагранжа, получим f(х₂) > f(х₁), так как на этот раз .

Замечание. Подчеркнем, что положительность (отрицательность) производной на интервале (а,b) не является необходимым условием возрастания (убывания) функции f(x) на интервале (а,b). Так, функция возрастает на интервале (0,4), но производная этой функции = 3(х – 2)² не является всюду положительной на этом интервале (она обращается в нуль в точке х = 2). Вообще, легко доказать, что функция f(x) возрастает (убывает) на интервале (а,b), если производная этой функции положительна (отрицательна) всюду на этом интервале, за исключением конечного числа точек, в которых эта производная равна нулю.

Установленную теоремой 2 связь между знаком производной и направлением изменения функции легко понять из геометрических соображений. Поскольку производная равна угловому коэффициенту касательной к графику функции y = f(x), знак производной указывает, острый или тупой угол с положительным направлением оси Oх составляет луч касательной, лежащий в верхней полуплоскости, т.е. наклонена ли касательная вверх или вниз, а с нею – идет ли вверх или вниз и сама кривая (рис.20).

Однако в отдельных точках x = x₀ касательная при этом может оказаться и горизонтальной (рис.20), т.е. производная – даже в строгом смысле – монотонно возрастающей (убывающей) функции может для отдельных значений x = x₀ обращаться в нуль.

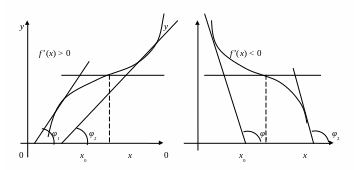
Рис. 20

4.3. Формула Коши (обобщенная формула конечных приращений)

В этом пункте мы докажем теорему, принадлежащую Коши и обобщающую установленную выше теорему Лагранжа.

Теорема Коши. Пусть функции f(x) и g(x): 1) непрерывны на сегменте [a,b], 2) существуют конечные производные и в каждой точке интервала (а,b), 3) производная функции g(x) на интервале (а,b) не обращается в нуль, тогда в интервале (а,b) найдется такая точка , что справедлива формула

, (3.36)

т.е. отношение приращений функций на данном отрезке равно отношению их производных в точке . Формулу (3.36) называют обобщенной формулой конечных приращений или формулой Коши.

Доказательство. Установим вначале, что знаменатель левой части равенства (3.36) не равен нулю, так как в противном случае это выражение не имело бы смысла. Если бы было g(b) = g(a), то для функции g(x) были бы выполнены на сегменте [a,b] все условия теоремы Ролля и по этой теореме внутри сегмента [a,b] нашлась бы такая точка , что = 0. Последнее противоречит условию 3) теоремы; значит, g(b)  g(a).