§4. Основные теоремы дифференциального исчисления

4.1. Теорема Ролля (теорема о корнях производной)

_{Теорема Ролля. Если функция y = f(х): 1) определена и непрерывна на сегменте [a,b], 2) дифференцируема в каждой точке интервала (a,b), 3) на концах сегмента принимает равные значения f (a) = f (b), то внутри сегмента [a,b] найдется по крайней мере одна точка ξ, производная в которой f ′(ξ) равна нулю.}

_{С геометрической точки зрения это означает, что внутри сегмента найдутся такие точки ξ, что касательная к кривой в этих точках параллельна оси Ох (рис.18).}

_{Доказательство. Так как функция f(х) непрерывна на отрезке [a,b], то, по 2-ой теореме Вейерштрасса (гл.1, §12, п.12.9), она имеет на этом отрезке наибольшее значение М и наименьшее значение m (рис.18).}

_{Если M = m, то функция f(х) при всех значениях х из промежутка [a,b] имеет постоянную величину f(х) = f(a) = f(b) = М. Но тогда в любой точке отрезка будет f ′(x) = 0, и теорема доказана.}

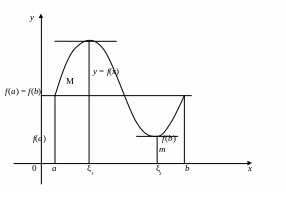
_{Рис. 18}

_{Предположим, что M  m. Мы знаем, что оба эти значения функцией достигаются, но, так как f(a) = f(b), то хоть одно из них достигается в некоторой точке ξ между а и b. Для определенности предположим, что f(ξ) = М. Тогда, так как f(ξ) – наибольшее значение функции, то f(ξ + x) – f(ξ)  0 как при Δх  0, так и при x  0.}

_{Отсюда следует, что}

_{при x  0,}

_{при x  0.}

_{Так как по условию теремы производная при х = ξ существует, то, переходя к пределу при x  0, получим}

_{при x  0,}

_{при x  0.}

_{Но соотношения f ′(ξ) ≤ 0 и f ′(ξ) ≥ 0 совместимы лишь в том случае, если f ′(ξ) = 0. Следовательно, внутри отрезка [a,b] имеется точка ξ, в которой производная f ′(ξ) = 0.}

_{Замечания: 1. Из доказательства теоремы Ролля вытекает справедливость следующего утверждения, которое носит название теоремы Ферма.}

_{Теорема Ферма. Пусть функция f(х) определена в некотором промежутке [a,b] и во внутренней точке  этого промежутка принимает наибольшее (наименьшее) значение. Если существует конечная производная f ′(ξ) в этой точке, то необходимо f ′(ξ) = 0.}

_{2. Точек, в которых производная функции равна нулю, может быть больше одной.}

_{Например, функция у = sin х:}

1. _{на сегменте [0,2 непрерывна}

2. _{имеет производную на интервале (0,2);}

3) f (0) = f (2) = 0;

у' = cosx, cosx = 0, при .

Таким образом, на [0,2 имеются две точки , в которых f ' = 0.

3. Если функция не удовлетворяет хотя бы одному из трех условий теоремы, то теорема не выполняется.

Например, функция x,

1. непрерывна на сегменте , 2) f (1) = f (1) = 1,

Но в точке х = 0 заданная функция производной не имеет. Для этой функции теорема Ролля на  не выполняется.

4.2. Формула Лагранжа (формула конечных приращений)

Большое значение в анализе и его приложениях имеет следующая теорема, принадлежащая Лагранжу.

Теорема Лагранжа. Если функция у = f(х):

1. непрерывна на сегменте [a,b],

2. дифференцируема в каждой точке интервала (a,b), то внутри сегмента [a,b] существует, по крайней мере, одна такая точка ξ, что справедлива формула

где а < ξ < b. (3.31)

Формулу (3.31) которую обычно записывают в виде

(3.32)

называют формулой Лагранжа или формулой конечных приращений. Подчеркнем, что в формуле (3.31) и (3.32) не обязательно считать, что b > a.

Геометрическая интерпретация теоремы дана на рис.19. Отношение равно угловому коэффициенту k = tg секущей, проходящей

через точки А(а, f(a)) и В(b, f(b)) кривой у = f(х), а есть угловой коэффициент касательной к кривой у = f(х), проходящей через точку С(ξ, f(ξ)). Формула Лагранжа (3.31) означает, что на кривой у = f(х) между точками А и В найдется такая точка С, касательная в которой параллельна секущей АВ.

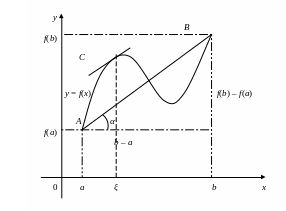
Рис. 19

Заметим, что теорема Ролля является частным случаем теоремы Лагранжа (при f(а) = f(b) и касательной параллельной оси Ох). Теорему Лагранжа называют также теоремой о среднем значении (в дифференциальном исчислении).

Доказательство. Рассмотрим на сегменте [a,b] следующую вспомогательную функцию:

(3.33)

Эта функция удовлетворяет всем условиям теоремы Ролля. В самом деле, она непрерывна в [a,b], так как представляет собой разность между непрерывной функцией f(х) и линейной функцией. В интервале (a,b) она имеет определенную конечную производную, равную

Наконец, непосредственной подстановкой в формулу (3.33) убеждаемся, что , т.е. F(x) принимает равные значения на концах промежутка.

Следовательно, к функции F(x) можно применить теорему Ролля и утверждать существование в (a,b) такой точки ξ, что = 0. Таким образом, что и требовалось доказать.

Часто удобно бывает записывать формулу Лагранжа в виде, несколько отличном от (3.32). Пусть f(x) удовлетворяет условиям теоремы Лагранжа. Зафиксируем любое х₀ из сегмента [a,b] и зададим ему приращение Δх произвольное, но такое чтобы значение (х₀+Δх) также лежало на сегменте [a,b]. Применим формулу Лагранжа к сегменту [х₀, х₀ +Δх] при Δх > 0. Число ξ, заключенное в этом случае между х₀ и х₀ + Δх, можно представить так: , где 0 < θ < 1. Тогда формула Лагранжа примет вид:

или (0 < θ <1). (3.34)

Формула Лагранжа в виде (3.34) дает точное выражение для приращения функции через вызвавшее его произвольное конечное приращение Δх аргумента. Отсюда проистекает и самое название «формула конечных приращений». Эта формула противопоставляется приближенному равенству (§2, п.2.1):

относительная погрешность которого стремится к нулю лишь при бесконечно малом Δх. Некоторым неудобством формулы Лагранжа является то, что в ней фигурирует неизвестное нам число (или ). Это не мешает, однако, многообразным применением этой формулы в анализе. В качестве примера рассмотрим следующие утверждения, справедливость которых непосредственно вытекает из формулы Лагранжа.