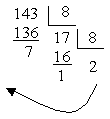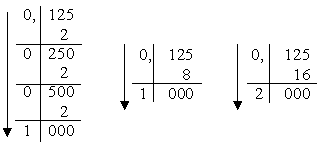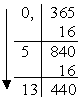Переведення чисел із десяткової системи числення у будь-яку іншу
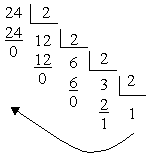
Переведення цілого числа з десяткової системи числення у будь-яку іншу здійснюється шляхом послідовного ділення числа на основу нової системи числення. Ділення виконується до тих пір, поки остання частка не стане менше дільника. Отримані остачі від ділення, взяті у зворотному порядку, будуть значеннями розрядів числа в новій системі числення. Остання частка дає старшу цифру числа.
Приклад: (24)10 = (?)2 |
|
(24)10 = (11000)2 |
Приклад: (143)10 = (?)8 |
|
(143)10 = (217)8 |
Приклад: (687)10 = (?)16 |
|
(687)10 = (2AF)16 |
Для переведення правильного дробу з десяткової системи числення у будь-яку іншу потрібно помножити заданий дріб на основу нової системи числення. Отримана ціла частина добутку буде першою цифрою після коми дробу в новій системі числення. Далі по черзі множаться дробові частини добутків на основу нової системи. Отримані цілі частини добутків будуть цифрами дробу у новій системі числення. Цей процес продовжують до тих пір, поки не буде знайдено число із заданою точністю.
Приклад: ( 0,125 )10 = ( ? )2; ( 0,125 )10 = ( ? )8; ( 0,125 )10 = ( ? )16. |
|
( 0,125 )10 = (0,001)2; ( 0,125 )10 = (0,1)8; ( 0,125 )10 = (0,2)16. |
Приклад: (0,365)10 = (?)16 |
|
(0,365)10 = (0,5D)16 |
Для переведення змішаного числа з десяткової системи числення в іншу необхідну окремо перевести цілу й дробову частини за вказаними правилами, а потім об'єднати результати у змішане число.
Переведення чисел із будь-якої системи числення в десяткову
Для переведення чисел із будь-якої системи числення в десяткову необхідно це число представити у вигляді полінома і розкрити всі члени полінома в десятковій системі числення.
Приклад: |
|
Приклад: |
|
Приклад: |
|
Переведення чисел із двійкової системи числення у вісімкову, із двійкової у шістнадцяткову і навпаки
Для переведення двійкового числа у вісімкову систему числення необхідно розбити двійкове число на тріади ( групи по три розряди ) вправо й вліво від коми, доповнюючи крайні тріади до повних нулями. Далі переводять кожну тріаду із двійкової системи числення у вісімкову.
При переведенні вісімкового числа у двійкову систему числення кожна вісімкова цифра записується двійковою тріадою (див. табл. 1).
Приклад: (111001,011000)2 = (71,30)8
Таблиця 1 |
|
Вісімкова цифра |
Тріада у коді 4-2-1 |
0 |
000 |
1 |
001 |
2 |
010 |
3 |
011 |
4 |
100 |
5 |
101 |
6 |
110 |
7 |
111 |
При переведенні вісімкового числа у двійкову систему числення кожна вісімкова цифра записується двійковою тріадою.
Приклад: |
(57,371)8 = (1011111,011111001)2 |
Аналогічно виконується переведення чисел із двійкової системи числення у шістнадцяткову систему числення і навпаки. При цьому для кожної шістнадцяткової цифри ставиться у відповідність двійкова тетрада (див табл. 2).
Таблиця 2 |
|
Шістнадцяткова цифра |
Тетрада у коді 8-4-2-1 |
0 |
0000 |
1 |
0001 |
2 |
0010 |
3 |
0011 |
4 |
0100 |
5 |
0101 |
6 |
0110 |
7 |
0111 |
8 |
1000 |
9 |
1001 |
A |
1010 |
B |
1011 |
C |
1100 |
D |
1101 |
E |
1110 |
F |
1111 |
Приклади: |
(5F,1)16 = (01011111,0001)2 (000010110001,1101)2 = (0B1,C)16 |