25. Граничні значення інтеграла типу Коші.

Теорема 1. Нехай – гладкий замкнений жорданоіий шлях є межею області , яка містить точку , і функція задовольняє умову

, (1)

, ,

Тоді функція є голоморфною в кожній із областей і , і для кожної точки справедливі формули Сохоцького

, , (2)

, , (3)

де

, , .

Доведення. Голоморфність випливає із властивостей інтеграла типу Коші. Крім цього, і, враховуючи, що

, ,

отримуємо

, , ,

, .

Завдяки умові (1) останній інтеграл існує в звичайному розумінні і для

та маємо

. (4)

Розіб’ємо на дві частини. Нехай – та частина , яка лежить в , а -та, що лежить зовні . Тоді останній інтеграл дорівнює сумі ,

, .

Використовуючи умову (1) отримуємо

.

Крім цього, якщо і , то , . Тому

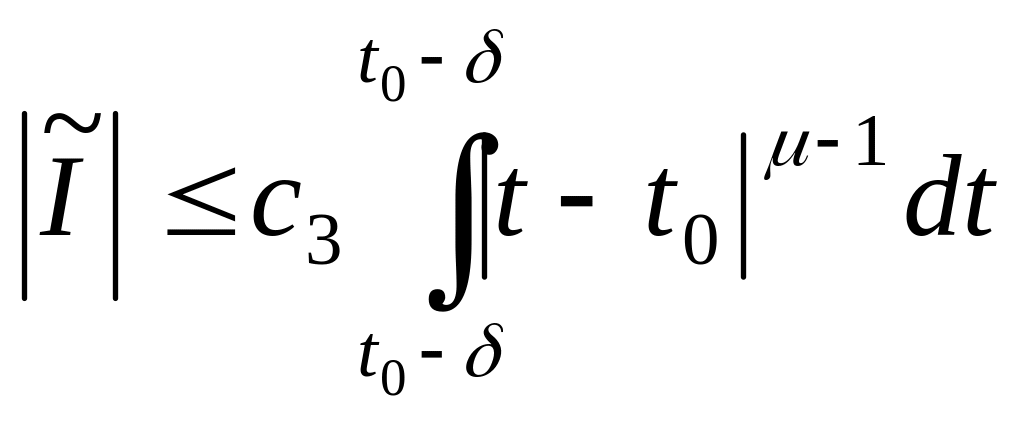
і при цьому , якщо . З іншого боку,

,

де –відстань між і , а – відстань між відстань між і . Бачимо, що для заданого можна так підібрати , що для всіх достатньо близьких до буде виконуватись і . Тому із (4) отримуємо першу із рівностей (2), а друга доводиться аналогічно. Рівності (3) безпосередньо випливають із (2). ►

26. Ріманова поверхня повної аналітичної функції. Ріман запропонував об’єкти, на яких повні аналітичні функції можна розглядати як однозначні. Ці об’єкти дістали назву ріманових поверхонь. Розглянемо множину , точками якої є всі канонічні елементи функції . -околом точки називається множина тих точок , для яких b лежить в деякому -околі точки і f_b є безпосереднім аналітичним продовженням f_a . Множина називається рімановою областю існування функції . Відображення , яке точці ставить у відповідність точку , тобто центр круга збіжності відповідного канонічного елемента, називається проекцією на , а точка а – проекцією точки . Відображення не є, взагалі кажучи, взаємно однозначним. Проте, якщо -правильна точка функції , то звуження на деякий окіл точки є взаємно однозначним. Цей окіл називається відміченим околом точки або її параметричним околом, а відображення , визначене рівністю , –параметричним або відміченим відображенням. Круг називається параметричним кругом, а відображення , задане формулою , –відображенням сусідства. Якщо -точка розгалуження порядку , тобто якщо –алгебраїчний або полярно критичний елемент, то відповідне параметричне відображення, визначається рівністю . Упорядкована пара ріманової області існування функції і відображення називається рімановою накриваючою поверхнею. Відображення називається також накриттям площин . Упорядкована пара ріманової області існування функції і сукупності вказаних вище параметричних відображеннь називається рімановою поверхнею функції . Одна точка може бути проекцією не більше, ніж скінченного або зліченного числа точок . Область називається простим листом ріманової поверхні , якщо відображення є однолистим. Ріманова поверхня однозначних функцій складається із одного листа. Ріманові поверхні n-значних функцій – із n-листів. При цьому в точку проектуються n-точок із . Інакше кажуть, що над точкою лежить n точок поверхні. Ріманова поверхня повної аналітичної функції є хаусдорфовим топологічним простором , кожна точка якого має окіл, який можна взаємно однозначно відобразити на . Якщо круги і канонічних і елементів фунції склеювати, тобто утотожнювати, по їх перетину у випадку, коли ці канонічні елементи є безпосереднім аналітичним продовженням один одного, то прийдемо до моделі ріманової поверні функції F . Для функцій і ці моделі були вже нами розглянуті.

27. Абстрактна ріманова поверхня. Абстрактною рімановою поверхнею називається зв’язний підпростір гаусдорфого топологічного простору , для кожної точки якого існує окіл та взаємно однозначне і неперервне відображення таке, що і для будь-яких двох околів і , перетин яких непорожний, функція , визначкна рівністю , є голоморфною в області . Функція називається відображенням сусідства, –параметричним кругом, –параметричним околом точки , а –параметричним відображенням. Таким чином, абстрактна ріманова поверхня –це двомірний багатовид, відображення сусідства якого є голоморфними функціями. Однозначна функція називається голоморфною на , якщо для кожної точки функція є голоморфною в деякому околі точки . Підкреслимо, що ріманова поверхня –це не тільки множина . Ріманова поверхня – це упорядкована пара підпростору і сукупності відповідних параметричних відображень. Один і той же підпростір можна перетворити в різні ріманаві поверхні вводячи різні параметричні відображення. При цьому дві абстрактні ріманові поверхні і називаються рівними, якщо існує топологічне, тобто неперервне і взаємно однозначне відображення , при якому для кожного функція , , є голоморфною в точці . Кожну абстрактну ріманову поверхню можна розглядати як ріманову поверхню деякої повної аналітичної функції. Докладніше про ріманові поверхні дивись в [ ].