
Розділ 6
Теорема
2.
Якщо
функція
![]() є однозначною і неперервною гілкою на
шляху
є однозначною і неперервною гілкою на
шляху
![]() функції
функції
![]() ,
аналітичної в області
,
аналітичної в області
![]() ,
то
,
то
![]() є аналітичною на
є аналітичною на
![]() .
.
Доведення.
Для кожного
![]() через
через
![]() позначимо такий канонічний елемент
функції
з центром в точці
позначимо такий канонічний елемент
функції
з центром в точці
![]() ,
для якого
,
для якого
![]() .
Таких елементів може бути декілька.
Оскільки
–
неперервна функція і згідно з теоремою
Пуанкаре різних канонічних елементів
з центром в заданій точці є скінченна
або зліченна кількість, то серед них
знайдеться такий (він єдиний), що для
всіх
.
Таких елементів може бути декілька.
Оскільки
–
неперервна функція і згідно з теоремою
Пуанкаре різних канонічних елементів
з центром в заданій точці є скінченна
або зліченна кількість, то серед них
знайдеться такий (він єдиний), що для
всіх
![]() з деякого проміжку
з деякого проміжку
![]() виконується
виконується
![]() (якщо
(якщо
![]() то беремо проміжок
то беремо проміжок
![]() ,
а якщо
,
а якщо
![]() ,
– то проміжок
,
– то проміжок
![]() ).
Ці проміжки є відкритими множинами в
просторі
).
Ці проміжки є відкритими множинами в
просторі
![]() і утворюють його відкрите покриття. З
нього можна виділити скінченне
підпокриття. Звідси і з означення
аналітичного продовження вздовж шляху
випливає твердження теореми.
►
і утворюють його відкрите покриття. З
нього можна виділити скінченне
підпокриття. Звідси і з означення
аналітичного продовження вздовж шляху
випливає твердження теореми.
►
Наслідок
2.
Для
того, щоб функція
була аналітичною на неперервному шляху
![]() ,
необхідно і достатньо, щоб вона була
неперервною гілкою на
деякої функції
,
аналітичної в області
,
необхідно і достатньо, щоб вона була
неперервною гілкою на
деякої функції
,
аналітичної в області
![]() .
.
Наслідок
3.
Якщо
функція
є аналітичною на неперервному шляху
і
![]() – її початковий канонічний елемент, то
існують область
і клас
– її початковий канонічний елемент, то
існують область
і клас
![]() неперервних шляхів з початками в точці
неперервних шляхів з початками в точці
![]() такій, що функція
такій, що функція
![]() є аналітичною в
.
є аналітичною в
.
Доведення.
Справді, такою областю
є обєднання
кругів
![]() ,
де
,
де
![]() ,
,
![]() і
і
![]() ,
збіжності рядів Тейлора канонічних
елементів
,
збіжності рядів Тейлора канонічних
елементів
![]() ,
за допомогою яких здійснюється аналітичне
продовження
вздовж
.
Множину
утворюють ті неперервні шляхи
,
за допомогою яких здійснюється аналітичне
продовження
вздовж
.
Множину
утворюють ті неперервні шляхи
![]() з початками в точці
з початками в точці
![]() ,
для яких існують точки
,
для яких існують точки
![]() ,
,![]() ,такі,
що
,такі,
що
![]() і
і
![]() ,
.
►
,
.
►
Отож,
для кожної функції
,
аналітичної на неперервному шляху
![]() ,
існує єдина повна аналітична функція
,
для якої
є неперервною гілкою на
.
Тому функцію
,
аналітичну на шляху
,
яка є неперервною гілкою на
повної аналітичної функції
,
позначають також через
,
існує єдина повна аналітична функція
,
для якої
є неперервною гілкою на
.
Тому функцію
,
аналітичну на шляху
,
яка є неперервною гілкою на
повної аналітичної функції
,
позначають також через
![]() ,
а також так
,
а також так
![]() .
.
Теорема
3.
Нехай
– загальна аналітична функція і її
канонічний елемент
допускає аналітичне продовження вздовж
неперервного шляху
,
то на
існує неперервна гілка
функції
така, що
![]() ,
де
.
Ця функція
є аналітичною функцією на
і
– її початковий елемент.
,
де
.
Ця функція
є аналітичною функцією на
і
– її початковий елемент.
Доведення.
Нехай
![]() ,
,
– ланцюг канонічних елементів, за
допомогою якого здійснюється аналітичне
продовження
вздовж
.
Шуканою функцією є функція
визначена рівністю
,
,
– ланцюг канонічних елементів, за
допомогою якого здійснюється аналітичне
продовження
вздовж
.
Шуканою функцією є функція
визначена рівністю
![]() ,
,
![]() ,
,
![]() ,
де
,
де
![]() –
такі точки, що
–
такі точки, що
![]() і
,
і
,
![]() ,
а
–
канонічні елементи за допомогою яких
здійснюються аналітичні продовження
вздовж
.
Отож, якщо функція
–
неперервна на неперервному шляху
,
а
–
канонічні елементи за допомогою яких
здійснюються аналітичні продовження
вздовж
.
Отож, якщо функція
–
неперервна на неперервному шляху
![]() ,
то
,
то
![]() ,
де
–
результат аналітичного продовження
вздовж звуження
на
,
де
–
результат аналітичного продовження
вздовж звуження
на
![]() .►
.►
Приклад
1.
Функція
![]() ,
,
![]() ,
є аналітичною на колі
,
є аналітичною на колі
![]() ,
,
і є неперервною гілкою на цьому колі
функції
,
,
і є неперервною гілкою на цьому колі
функції
![]() з
початковим елементом з центром в точці
4, який в цій точці приймає значення 2.
з
початковим елементом з центром в точці
4, який в цій точці приймає значення 2.
18.
Голоморфна
первісна.
Голоморфною
або однозначною первісною функції
![]() в області
називається така голоморфна в
функція F,
що
в області
називається така голоморфна в
функція F,
що
![]() .
.
Теорема 1. Якщо функція має голоморфну первісну в області , то є голоморфною в .
Доведення.
Справді, F
є голоморфною в
.
Тому голоморфними в
є
і
всі її похідні. Але
![]() .
Отже,
є
голоморфною в D.
►
.
Отже,
є
голоморфною в D.
►
Теорема 2. Для того, щоб функція була голоморфною в однозв’язній області , необхідно і достатньо, щоб вона мала в голоморфну первісну.
Доведення.
Якщо
є
голоморфною в однозв'язній області
,
то на підставі теореми Коші інтеграл
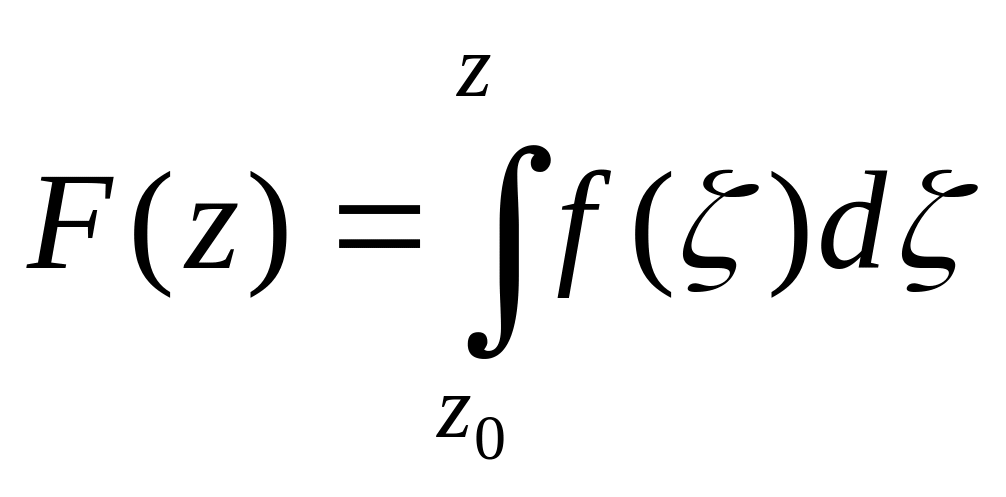 не
залежить в
від шляху інтегрування і (дивись доведення
теореми Морери) функція
не
залежить в
від шляху інтегрування і (дивись доведення
теореми Морери) функція
![]() є голоморфною первісною функції
в області
.
Тому необхідна частина теореми доведена,
а достатня випливає із попередньої
теореми. ►
є голоморфною первісною функції
в області
.
Тому необхідна частина теореми доведена,
а достатня випливає із попередньої
теореми. ►
Теорема
3.
Якщо
голоморфна в області
функція f
має
в
голоморфну
первісну ,
то для будь-яких точок
![]() і
і
![]()
![]() (5)
(5)
і інтеграл (5) не залежить в від шляху інтегрування.
Доведення.
Справді, нехай
![]() – гладкий шлях із початком в точці
– гладкий шлях із початком в точці
![]() і
кінцем в точці
і
кінцем в точці
![]() ,
а
,
а
![]() .
Тоді
.
Тоді
![]() ,
тобто функція
,
тобто функція
![]() є звичайною первісною функції
на
будь-якому гладкому шляху
.
Тому
є звичайною первісною функції
на
будь-якому гладкому шляху
.
Тому
![]() .
.
Звідси випливає (5) і незалежність інтеграла (5) в від шляху інтегрування. ►
Теорема
4.
Якщо
функція
,
голоморфна в області
,
має в
голоморфну первісну
![]() ,
то голоморфною первісною
в D
є також функція
,
то голоморфною первісною
в D
є також функція
, ![]() ,
(6)
,
(6)
й
існує стала с така, що
![]() .
.
Доведення.
Справді, з попередньої теореми випливає,
що інтеграл (6) не залежить в D
від шляху інтегрування. Тому (див.
доведення теореми Морери) функція F
є також голоморфною первісною
.
Отже,
![]() ,
якщо
,
якщо
![]()
Звідси та з умов Коші-Рімана отримуємо
Звідси та з умов Коші-Рімана отримуємо
![]() ,
,
де
![]() і
і
![]() .
Тому W
є сталою функцією і теорема 4 доведена.
►
.
Тому W
є сталою функцією і теорема 4 доведена.
►
Приклад
1. Функція
![]() є голоморфною первісною в
є голоморфною первісною в
![]() функції
функції
![]() .
.
19.
Аналітична первісна.
Аналітичною або багатозначною первісною
функції
називається така аналітична функція
![]() ,
що для кожної точки
,
що для кожної точки
![]() існують
існують
![]() -окіл
-окіл
![]() і голоморфна гілка
і голоморфна гілка
![]() функції
в
,
для яких
функції
в
,
для яких
![]()
Теорема
1.
Для
того, щоб неперервна в області
функція
мала
аналітичну первісну, необхідно і
достатньо, щоб
була
голоморфною в області D.
Якщо ця умова виконана, то аналітичною
первісною є функція![]() , де
, де
![]()
і
Г – клас шляхів з початками в точці
![]() таких, що для кожної точки
знайдеться
таких, що для кожної точки
знайдеться
![]() з кінцем в точці
з кінцем в точці
![]() .
Якщо
.
Якщо
![]() – інша аналітична первісна функції
з такою ж множиною шляхів Г, то існує
стала
– інша аналітична первісна функції
з такою ж множиною шляхів Г, то існує
стала
![]() , для якої
, для якої
![]() ,
тобто
,
тобто
![]() .
.
Доведення.
Необхідність випливає безпосередньо
з означення та нескінченної диференційовності
голоморфних функцій. Далі, якщо
є
голоморфною в D,
то
![]() є голоморфною первісною
в
деякому крузі
є голоморфною первісною
в
деякому крузі
![]() .
Якщо
– довільна точка області і
– шлях, який з’єднує точки а
та b,
то результат аналітичного продовження
.
Якщо
– довільна точка області і
– шлях, який з’єднує точки а
та b,
то результат аналітичного продовження
![]() вздовж
має вигляд
вздовж
має вигляд
![]() ,
,
звідси
випливає (1) і достатність доведена. Якщо
– інша аналітична первісна,
то в деякому околі точки a
маємо![]() .
Тому
.
Тому
![]() і
і
![]() є голоморфними первісними функції
в
крузі
.
Отже, за відповідною теоремою для
голоморфних первісних існує стала
є голоморфними первісними функції
в
крузі
.
Отже, за відповідною теоремою для
голоморфних первісних існує стала
![]() , за якої
, за якої
![]() в
цьому крузі.
►
в
цьому крузі.
►
Приклад
1. Функція
![]() є аналітичною первісною в
є аналітичною первісною в
![]() функції
функції
![]() .
.
20.
Первісна аналітичної функції. Первісною
функції
![]() ,
аналітичної в області
,
називається аналітична в області
функція
,
аналітичної в області
,
називається аналітична в області
функція
![]() ,
для якої
є голоморфною первісною
.
,
для якої
є голоморфною первісною
.
Теорема
3.
Нехай
канонічний елемент
з центром у точці
допускає аналітичне продовження вздовж
спрямлюваного шляху
і
.
Тоді канонічний елемент
![]() ,
також допускає аналітичне продовження
вздовж
і результатом
аналітичного
продовження є
,
також допускає аналітичне продовження
вздовж
і результатом
аналітичного
продовження є
![]() ,
,
де
![]() ,
,
![]() –
довільний спрямлюваний шлях з початком
в точці
,
який є гомотопним шляху
в області, яка є обєднанням
кругів збіжності канонічних елементів,
за допомогою яких здійснюється аналітичне
продовження
вздовж
,
а
– функція, аналітична на
–
довільний спрямлюваний шлях з початком
в точці
,
який є гомотопним шляху
в області, яка є обєднанням
кругів збіжності канонічних елементів,
за допомогою яких здійснюється аналітичне
продовження
вздовж
,
а
– функція, аналітична на
![]() ,
з початковим елементом
.
,
з початковим елементом
.
Доведення.
Досить довести теорему у випадку, коли
![]() ,
а в цьому випадку твердження випливає
безпосередньо з прикладу 6.3.2.
►
,
а в цьому випадку твердження випливає
безпосередньо з прикладу 6.3.2.
►
Теорема
2.
Кожна
функція
,
аналітична в області
,
має первісну. Однією з її первісних є
функція
![]() ,
де
,
де
,
а
для кожної іншої первісної
![]() існує стала
існує стала
![]() така, що
,
тобто
така, що
,
тобто
![]() .
.
Доведення.
Ця
теорема випливає безпосередньо з
означень, оскільки
![]() в деякому околі точки
.►
в деякому околі точки
.►
Теорема
3.
Якщо
первісна функції
![]() ,
аналітичної в області
,
,
аналітичної в області
,
![]() і
і
![]() та
– результати
аналітичних
продовжень вздовж
функцій
та
відповідно, то
є голоморфною первісною
.
та
– результати
аналітичних
продовжень вздовж
функцій
та
відповідно, то
є голоморфною первісною
.
Доведення. Це твердження випливає з попередніх двох теорем. ►
Приклад
1.
Кожна повна аналітична функція виду
![]() ,
де
,
де
![]() -стала,
є первісною повної аналітичної функції
-стала,
є первісною повної аналітичної функції
![]() .
.
21.
Первісна функції, аналітичної на шляху.
Первісною
функції
![]() ,
аналітичної на спрямлюваному
шляху
,
з початковим елементом
називається така аналітична на
функція
,
аналітичної на спрямлюваному
шляху
,
з початковим елементом
називається така аналітична на
функція
![]() ,
початковий елемент
якої є голоморфною первісною початкового
елемента
.
,
початковий елемент
якої є голоморфною первісною початкового
елемента
.
Теорема
1.
Кожна
функція
з
початковим елементом
,
аналітична на неперервному шляху
![]() ,
має первісну. Однією з її первісних є
функція
,
аналітична на шляху
,
з початковим елементом
,
а для кожної іншої первісно
,
має первісну. Однією з її первісних є
функція
,
аналітична на шляху
,
з початковим елементом
,
а для кожної іншої первісно
![]() існує стала
така, що
існує стала
така, що
![]() .
.
Теорема 2. Якщо є первісною функції , аналітичної на неперервному шляху , то функція є голоморфною первісною функції , де і кінцеві елементи функцій і , відповідно.
Теорема
3.
Якщо
![]() є первісною функції
є первісною функції
![]() ,
аналітичної на неперервному шляху
,
то
,
аналітичної на неперервному шляху
,
то
![]() є неперервною гілкою на
деякої первісної функції
,
аналітичної в деякій такій області
,
що
є неперервною гілкою на
деякої первісної функції
,
аналітичної в деякій такій області
,
що
![]() ,
де
–
початковий канонічний елемент функції
.
,
де
–
початковий канонічний елемент функції
.
Ці три теореми є наслідками результатів попередніх пунктів.
Теорема
4.
Якщо
![]() є первісною функції
,
аналітичної на спрямлюваному шляху
,
то
є первісною функції
,
аналітичної на спрямлюваному шляху
,
то
![]() , (1)
, (1)
тобто
![]() ,
(2)
,
(2)
де
![]() ,
,
![]() .
.
Доведення.
Нехай
–
початковий канонічний елемент функції
,
а
![]() ,
,![]() ,
–
ланцюг канонічних елементів, за допомогою
якого здійснюється аналітичне продовження
вздовж
і
,
–
ланцюг канонічних елементів, за допомогою
якого здійснюється аналітичне продовження
вздовж
і
![]() – множина точок таких, що
і для
виконується
– множина точок таких, що
і для
виконується
![]() .
Якщо шлях
є гладким, то
.
Якщо шлях
є гладким, то
![]() ,
тобто
є звичайною первісною. Тому в цьому
випадку (1) виконується. Якщо
– довільний спрямлюваний шлях, то
позначимо через
,
тобто
є звичайною первісною. Тому в цьому
випадку (1) виконується. Якщо
– довільний спрямлюваний шлях, то
позначимо через
![]() гладкий шлях, який є гомотопним в
гладкий шлях, який є гомотопним в
![]() звуженню
на
звуженню
на
![]() .
Тоді на підставі теореми Коші
.
Тоді на підставі теореми Коші
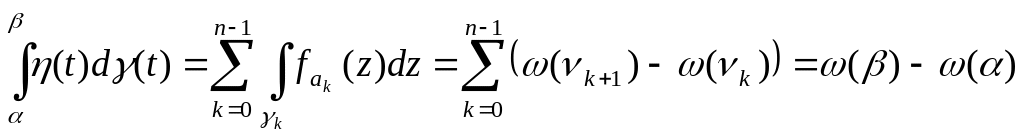
і теорема доведена. ►
Теорема
5.
Для
того, щоб функція
була первісною функції
,
аналітичної на гладкому шляху
,
необхідно і достатньо, щоб
![]() для всіх
для всіх
![]() ,
тобто щоб
була звичайною первісною функції
на
.
,
тобто щоб
була звичайною первісною функції
на
.
Доведення.
Необхідність. Нехай
є первісною функції
,
аналітичної на
.
Тоді для кожного
![]() знайдеться окіл
знайдеться окіл
![]() і голоморфні в деякому крузі
і голоморфні в деякому крузі
![]() функції
функції
![]() та
та
![]() такі,
такі,
![]() для всіх
для всіх
![]() і
і
![]() для всіх
для всіх
![]() ,
тобто
є звичайною первісною функції
на
.
Навпаки, якщо
є
звичайною первісною функції
на на гладкому шляху
,
то для кожного
знайдеться окіл
і
голоморфні в деякому крузі
функція
,
тобто
є звичайною первісною функції
на
.
Навпаки, якщо
є
звичайною первісною функції
на на гладкому шляху
,
то для кожного
знайдеться окіл
і
голоморфні в деякому крузі
функція
![]() такі, що
такі, що
![]() і
і
![]() для всіх
.
Нехай
для всіх
.
Нехай
![]()
Тоді
![]() допускає аналітичне продовження вздовж
і
результат аналітичного продовження
вздовж звуження
допускає аналітичне продовження вздовж
і
результат аналітичного продовження
вздовж звуження
![]() шляху
на
шляху
на
![]() має
вигляд
має
вигляд
![]()
Крім цього, для всіх і
![]()
для
всіх
з
делякого околу точки
![]() .
Тому
є також первісною функції
,
аналітичної на
.►
.
Тому
є також первісною функції
,
аналітичної на
.►
Приклад 1. Функція , , є аналітичною на колі , , і є неперервною гілкою на цьому колі функцій з початковим елементом з центром в точці 4, який в цій точці приймає значення 2,
![]() .
.
Водночас,
функція
![]() є первісною функції
є первісною функції
![]() ,
аналітичної на
,
і
,
аналітичної на
,
і
![]() .
з іншого боку, функція
.
з іншого боку, функція
![]() є первісною повної аналітичної функції
.
Функція
є первісною повної аналітичної функції
.
Функція
![]() ,
,
є аналітичною гілкою функції
на
,
,
,
є аналітичною гілкою функції
на
,
![]() і
і
![]() .
.
Зауваження
1. Останній приклад показує, що рівність
(1) може бути не справедливою, якщо
![]() є неперервною гілкою на
аналітичної функції
,
а
є неперервною гілкою на
аналітичної функції
,
а
![]() – довільна однозначна гілка на
первісної
функції
.
Суть теореми 2 полягає в тому, що рівність
(2) справедлива, якщо
–та
гілка
,
яка є первісною
на
.
Разом з цим, справедливе наступне
твердження.
– довільна однозначна гілка на
первісної
функції
.
Суть теореми 2 полягає в тому, що рівність
(2) справедлива, якщо
–та
гілка
,
яка є первісною
на
.
Разом з цим, справедливе наступне
твердження.
Теорема 6. Якщо функція є аналітичною первісною f, голоморфної в області D, то для будь-якого спрямлюваного шляху , , виконується
![]() ,
(1)
,
(1)
де
![]() – будь-яка однозначна неперервна гілка
функції F
на
,
– будь-яка однозначна неперервна гілка
функції F
на
,
![]() і
і
![]() .
.
Доведення.
Справді, будь-який канонічний елемент
![]() функції
з центром в точці
має вигляд
функції
з центром в точці
має вигляд
![]() ,
,
а результат його аналітичного продовження вздовж шляху є таким
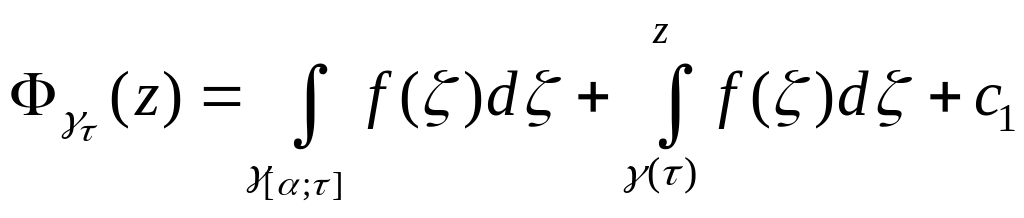 .
.
Тому
кожна однозначна гілка
![]() аналітичної первісної функції
має вигляд
аналітичної первісної функції
має вигляд
![]() ,
,
де – стала. Звідси випливає потрібний висновок. ►
Наслідок 1. Якщо –повна аналітична функція, яка є аналітичною первісною в області функції , голоморфної в , то для будь-якого спрямлюваного шляху виконується (1).
Зауваження 2. Суть теореми 3 полягає в тому, що якщо є голоморфною в , то формула (2) справедлива для кожної однозначної неперервної гілки функції на .
22.
Приріст функції на шляху.
Приростом функції (однозначної)![]() на шляху
називається число
на шляху
називається число
![]() ,
де
і
.
Таким чином, приріст однозначної функції
на шляху –це різниця значень функції
цієї в кінцевій та початковій точках
шляху. Приростом функції
,
де
і
.
Таким чином, приріст однозначної функції
на шляху –це різниця значень функції
цієї в кінцевій та початковій точках
шляху. Приростом функції
![]() на
шляху
називається число
на
шляху
називається число
![]() .
Якщо
є однозначною гілкою на
багатозачної функції
,
то знову можемо записати, що
.
Якщо
є однозначною гілкою на
багатозачної функції
,
то знову можемо записати, що
![]() .
Але тепер
.
Але тепер
![]() означає
те значення функції
в точці
,
яке приймає функція
в точці
означає
те значення функції
в точці
,
яке приймає функція
в точці
![]() ,
а
,
а![]() –
те значення функції
в точці
,
яке приймає функція
в точці
–
те значення функції
в точці
,
яке приймає функція
в точці
![]() .
Приростом канонічного елемента
.
Приростом канонічного елемента
![]() або приростом функції
або приростом функції
![]() ,
голоморфної в крузі
,
голоморфної в крузі
![]() ,
на шляху
такому, що
,
на шляху
такому, що
![]() ,
називається число
,
називається число
![]() ,
де
,
де
![]() і
і
![]() – результат аналітичного продовження
вздовж .
Різні канонічні елементи з центром в
точці а повної аналітичної функції F
на одному і тому ж шляху можуть мати
різні прирости. В цьому переконуємось
на прикладі функції
– результат аналітичного продовження
вздовж .
Різні канонічні елементи з центром в
точці а повної аналітичної функції F
на одному і тому ж шляху можуть мати
різні прирости. В цьому переконуємось
на прикладі функції
![]() .
Для цієї функції існують два різні
канонічні елементи Fa
з центром в точці
.
Для цієї функції існують два різні
канонічні елементи Fa
з центром в точці
![]() ,
які на шляху
,
які на шляху
![]() ,
,
мають прирости
,
,
мають прирости
![]() і
і
![]() .
Різні однозначні неперервні гілки
повної аналітичної на одному і тому ж
шляху також можуть мати різні прирости.
Проте для деяких функції ці прирости є
одинакові і тоді можна говорити про
приріст багатозначної функції на
заданому шляху.
.
Різні однозначні неперервні гілки
повної аналітичної на одному і тому ж
шляху також можуть мати різні прирости.
Проте для деяких функції ці прирости є
одинакові і тоді можна говорити про
приріст багатозначної функції на
заданому шляху.
23. Однозначні гілки і прирости логарифма і аргументу на шляху.
Теорема
1.
На
будь-якому спрямованому шляху
![]() ,
який не проходить через початок координат,
при будь-якому
,
який не проходить через початок координат,
при будь-якому
![]() існує єдина однозначна неперервна гілка
існує єдина однозначна неперервна гілка
![]() функції
функції
![]() на
така,
що
на
така,
що
![]() ,
причому
,
причому
![]() ,
, ![]() ,
(1)
,
(1)
і
![]() для всіх t
із деякого околу точки ,
де
для всіх t
із деякого околу точки ,
де
![]() – звуження
на
,
– результат аналітичного продовження
вздовж
тої однозначної гілки
– звуження
на
,
– результат аналітичного продовження
вздовж
тої однозначної гілки
![]() функції
в околі точки
функції
в околі точки
![]() ,
для якої
,
для якої
![]() .
.
Доведення.
Справді, функція ,
визначена рівністю (1), є неперервною на
.
Крім цього,
![]() .
Отже,
є шуканою неперервною гілкою. Справедливість
рівності
випливає із теореми 1.2, а єдиність – із
неперервності і того, що два різні
значення Ln
z
в одній точці відрізняються на
.
Отже,
є шуканою неперервною гілкою. Справедливість
рівності
випливає із теореми 1.2, а єдиність – із
неперервності і того, що два різні
значення Ln
z
в одній точці відрізняються на
![]() .►
.►
Наслідок 1. Приріст кожної неперервної однозначної гілки функції на спрямованому шляху , який не проходить через початок координат, дорівнює
![]()
і
цей приріст збігається із приростом на
будь-якого канонічного елемента функції
з
центром в точці а, а також з приростом
кожної первісної функції
![]() на шляху .
на шляху .
Наслідок
2.
На
будь-якому спрямованому шляху
,
який не проходить через початок координат,
при будь-якому
![]() існує єдина неперервна однозначна гілка
існує єдина неперервна однозначна гілка
![]() на шляху
функції
на шляху
функції
![]() така, що
така, що
![]() .
При цьому
.
При цьому
![]() ,
де
,
де
![]() -
та однозначна гілка
на ,
для якої
-
та однозначна гілка
на ,
для якої
![]() .
Цю гілку позначають також через
.
Цю гілку позначають також через
![]() .
.
Доведення.
Для отримання наслідку 2 досить врахувати
![]() .►
.►
Наслідок 3. Приріст кожної неперервної гілки функції
на спрямованому шляху , який не проходить через початок координат, дорівнює
![]() .
.
Це
число
![]() називається
приростом
на шляху
.
При цьому, якщо шлях
є
замкненим, то
називається
приростом
на шляху
.
При цьому, якщо шлях
є
замкненим, то
![]() .
.
Наслідок
4.
На
будь-якому спрямованому шляху
,
який не проходить через початок координат
при будь-якому
![]() існує єдина неперервна гілка
існує єдина неперервна гілка
![]() функції
функції
![]() така, що
така, що
![]() .
.
Доведення.
Справді, такою гілкою є функція
![]() ,де
,де
![]() та гілка
на
,
для якої Im(Ln
())=..►
та гілка
на
,
для якої Im(Ln
())=..►
Наслідок
5.
Якщо
функція
є голоморфною в області G,
то на будь-якому спрямованому шляху
![]() такому, що (z)0
для всіх z[],
існують однозначні і неперервні гілки
функцій
такому, що (z)0
для всіх z[],
існують однозначні і неперервні гілки
функцій
![]() ,
,![]() і
і
![]() ,
які в заданій точці приймають задані
значення із множини своїх значень в цій
точці. Зокрема, гілка
,
яка в точці
приймає задане значення
,
які в заданій точці приймають задані
значення із множини своїх значень в цій
точці. Зокрема, гілка
,
яка в точці
приймає задане значення
![]() ,
має вигляд
,
має вигляд
![]() ,
,
а
гілкою
функції
,
яка в точці
приймає значення
![]() ,
є функція
,
є функція
![]() .
.
Наслідок
6.
Нехай
функція
є голоморфною в області G
і
–
спрямований шлях такий, що
![]() при всіх
при всіх
![]() .
Тоді приріст кожної однозначної і
неперервної гілки
на
має
.
Тоді приріст кожної однозначної і
неперервної гілки
на
має
вигляд
![]() ,
а приріст кожної неперервної гілки
рівний
,
а приріст кожної неперервної гілки
рівний
![]() .
.
При
цьому якщо шлях
є замкнений, то
![]() .
.
Приклад 1. Нехай – гладкий шлях. Покажемо, що
![]() ,
,
![]() ,
,
і, якщо не проходить через початок координат, то
![]() ,
,
де
![]() –
така голоморфна гілка функції
в області
–
така голоморфна гілка функції
в області
![]() ,
що
,
що
![]() ,
де
,
і
–
шлях в
,
де
,
і
–
шлях в
![]() ,
заданий ормулою
,
заданий ормулою
![]() .
Справді, шлях
є образом шляху
при відображені,
його початок знаходиться в
.
Справді, шлях
є образом шляху
при відображені,
його початок знаходиться в
![]() ,
кінець в точці
,
кінець в точці
![]() і він не проходить через точку
і він не проходить через точку
![]() .
Тому функція
.
Тому функція
![]() є голоморфною в
є голоморфною в
![]() і
і
![]() .
.
Крім
цього, функція
![]() є
голоморфною первісною функції
є
голоморфною первісною функції
![]() в
в
![]() .
Отже,
.
Отже,
![]() ,
,
![]() .
.
З іншого боку,
![]() ,
.
,
.
Отже, існує стала для якої
![]() .
.
Але
![]() ,
,
![]() .
.
Тому
![]() і ми приходимо до потрібних рівностей.
і ми приходимо до потрібних рівностей.
24.
Інтеграл в розумінні головного значеня
по гладкому шляху. Нехай
–
гладкий жордановий шлях,
і
.
Тоді в кожній точці
![]() цей шлях має дотичну і для всіх досить
малих
цей шлях має дотичну і для всіх досить
малих
![]() коло
коло
![]() перетинає
перетинає
![]() тільки
в двох точках :
тільки
в двох точках :
![]() і
і
![]() ,
,
![]() .
Розглянемо звуження
.
Розглянемо звуження
![]() та
та
![]() шляху
на проміжки
шляху
на проміжки
![]() і
і
![]() відповідно.
Інтегралом в розумінні головного
значення функції
відповідно.
Інтегралом в розумінні головного
значення функції
![]() в точці
називається
границя
в точці
називається
границя
![]() .
.
Використовується також позначення
![]() .
.
Якщо
функція
ішнтегрованих на
,
то вона інтегрована на
і в розумінні головного значеня і обидва
шнтеграли збігаються. Тому для позначення
інтеграла в розумінні головного значення
використовують талож символ![]() .
.
Приклад 1. Нехай – замкнений жорданоіий гладкий шлях.. Покажемо, що
![]() ,
,
![]() ,
,
причому
береться знак
“+”,
якщо
задає
додатну орієнтацію області
![]() і
береться знак “
і
береться знак “![]() ”
у протилежному випадку. Справді, нехай
”
у протилежному випадку. Справді, нехай
![]() .
Тоді в першому випадку
.
Тоді в першому випадку
![]() ,
,
де
![]() -
та частина кола
,
яка входить в межу області
-
та частина кола
,
яка входить в межу області
![]() .
Якщо
.
Якщо
![]() ,
то
прямує до півкола. Тому
,
то
прямує до півкола. Тому
![]()
і ми приходимо до потрібного висновку.
Приклад 2. Нехай –замкнений жорданоіий гладкий шлях де , . Покажемо, що
![]() ,
,
,
,
де
![]() ,
,
![]() ,
–такий
замкнений жордановий гладкий шлях, що
,
–такий
замкнений жордановий гладкий шлях, що
![]() для
для
![]() і
задає
додатну орієнтацію області
і
задає
додатну орієнтацію області
![]() ,
а
–звуження
на
,
а
–звуження
на
![]() .
Справді,
.
Справді,
![]()
і залишилось скористатись попереднім прикладом.
