18. Построить на числовой плоскости множества , , . Найти множество .

19. Существуют ли такие множества А, В, С, что АВ, АС= и (АB)\C=?

20. Определить (графически), в каком отношении (XY, YX, Y=X) находятся множества X и Y, если: 1) X=A(B\C); Y=(AB)\(AC); 2) X=(AB)\C, Y=(A\C)(B\C); 3) X=A\(BC), Y=(A\B)(A\C).

21. Проверить справедливость включения (AC)\B(A\B)C

22. Доказать, что .

23. Доказать, что .

24. Доказать, что . Доказать тождества

- исходя из определений операций;

- на основе законов алгебры множеств.

Проиллюстрировать доказательство диаграммами Венна.

25. .

26. .

27. .

28. .

29. .

30. .

31. Определить операции , , \ через: 1)  и ; 2)  и ; \ и . Определить (если это возможно) \ через  и .

Доказать равенства:

32. .

33. .

34. .

35. .

36. .

37. .

38. .

39. .

40. .

41. .

42. Доказать, что сумма является полным квадратом.

Доказать неравенства:

43. .

44. .

45. .

46. .

47. .

48. .

49. .

Доказать делимость чисел:

50. .

51. .

52. .

53. .

54. .

55. .

56. Пусть положительные числа, такие, что . Доказать, что .

57. Пусть произвольные положительные числа. Доказать, что .

58. Пусть . Доказать, что .

59. Определить общий член последовательности, заданной рекуррентным соотношением , если а₁=0.

60. Сколько подмножеств имеет n-элементное множество?

61. Доказать, что любую сумму денег, большую 7 копеек, можно разменять монетами по 3 и 5 копеек.

62. На плоскости проведено n прямых, из которых никакие две не параллельны и никакие три не проходят через одну точку. На сколько частей они разбивают плоскость?

63. Доказать, что .

НЕЧЕТКИЕ МНОЖЕСТВА

64. Пусть U – множество дней недели. Выступая в роли эксперта, запишите следующие нечеткие множества: – начало недели; – середина недели; – конец недели; – не начало, но и не конец недели. Есть ли среди определенных Вами функций принадлежности унимодальные?

65. Пусть – возможный возраст человека. Выступая в роли эксперта, постройте графики функций принадлежности следующих нечетких множеств: – молодой; – старый; – очень молодой; – не старый. Сравните полученные Вами графики с графиками Ваших коллег. Если есть различия, попытайтесь объяснить причины этих различий.

66. Пусть U – множество дисциплин, изучаемых в текущем семестре. Присвойте номер каждой дисциплине и, выступая в роли эксперта, запишите следующие нечеткие множества: – мне нравится эта дисциплина; – я не понимаю эту дисциплину; – мне не нравится эта дисциплина; – я бы хотел изучать эту дисциплину глубже. Представьте разложение каждого из нечетких множеств по уровням.

67. Пусть U – множество неотрицательных действительных чисел, на котором заданы функции принадлежности следующих нечетких множеств: ; ; 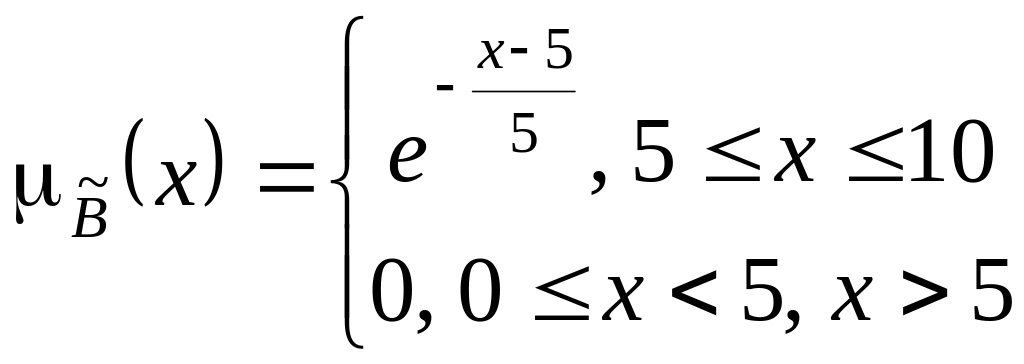; . Для каждого из этих множеств требуется:

- построить график функции принадлежности;

- записать разложение по множествам уровня;

- записать приближенное дискретное разложение, разбив отрезок [0, 1] на пять равных частей.

68. Пусть U – цены автомобилей, 4≤u≤5000 (у.е.). Выступая в роли эксперта, постройте графики функций принадлежности следующих нечетких множеств: – цены автомобилей для среднего класса; – цены автомобилей для богатых людей; – цены автомобилей для небогатых людей. Для каждой кривой запишите функцию принадлежности аналитически. Запишите разложения по множествам уровня каждого из нечетких множеств. Запишите приближенное дискретное разложение, разбив отрезок [0, 1] на десять равных частей.

69. Даны нечеткие множества: и . Требуется:

- записать множества ; ;

- сделать два чертежа: на одном изобразить множества , на втором – множества ;

- вычислить индексы нечеткости по метрике Хемминга для всех шести множеств;

- вычислить индексы нечеткости по евклидовой метрике для всех шести множеств.

70. Пусть – нечеткое множество, заданное на множестве неотрицательных действительных чисел функцией принадлежности . Требуется:

- записать множества ;

- построить графики функций принадлежности множеств ;

- вычислить индексы нечеткости по метрике Хемминга для всех трех множеств;

- вычислить индексы нечеткости по евклидовой метрике для всех трех множеств.

71. На универсальном множестве заданы нечеткие множества , , . Найти множества ; ; ; ; ; ; ; ; . Привести графическую интерпретацию выполненных операций.

72. На универсальном множестве U=[0, 3] заданы нечеткие множества и . Требуется:

- построить графики функций принадлежности;

- записать множества ; ; ; ; ; и построить графики их функций принадлежности.

73. Доказать, что для операций над нечеткими множествами выполняются законы ассоциативности, идемпотентности, поглощения, действия с константами, де Моргана, но не выполняются закон противоречия и закон исключения третьего (свойства дополняемости операций пересечения и объединения), т.е. в общем случае справедливы соотношения ; .

74. Даны нечеткие числа: а – «немного больше 3» и b – «примерно 3», если и . Выполнить арифметические операции и сравнить нечеткие числа с дискретными носителями.

75. Пусть является носителем следующих нечетких чисел: a – «в городе К проезд на метро стоит приблизительно 8 руб.»; b – «проезд на маршрутке в этом городе стоит приблизительно 15 руб.»; c – «мне надо проехать на метро раз пять»; d – «мне надо проехать на маршрутке, по крайней мере, раза три». Требуется:

- выступая в роли эксперта, записать нечеткие числа a, b, c, d в форме объединения точечных нечетких множеств;

-найти нечеткое число х – «примерная сумма расходов на транспорт в городе К»;

- разложить нечеткие числа a, b, c, d и х по множествам α-уровня, если ;

- построить графики функций принадлежности чисел a, b, c, d и х.

76. Пусть: а – «немного больше 3» и b – «примерно 5», причем ; . Требуется:

- разложить нечеткие числа a, b по множествам α-уровня, если ;

- построить графики функций принадлежности этих чисел, используя полученные разложения;

- записать функции принадлежности и построить их графики для чисел ;

- сравнить числа a и b.

77. Доказать, что нечеткие числа a и b являются числами -типа, если ; . Выполнить над ними все арифметические операции и сравнить эти числа.

78. Прибыль коммерческой фирмы формируется из выручки трех магазинов и некоторой статьи расходов. При анализе продаж магазинов было установлено следующее:

- первый магазин в течение месяца обеспечивает уровень продаж на сумму от 40 до 100 тыс. руб. в зависимости от величины спроса, но с наибольшей вероятностью можно ожидать сумму от 50 до 70 тыс. руб.;

- второй магазин надежно обеспечивает высокий уровень продаж на сумму 100 – 110 тыс. руб.;

- третий магазин ненадежен и обеспечивает уровень продаж не более 20 тыс. руб. в месяц.

Расходы могут находиться в пределах от 50 до 100 тыс. руб. в месяц, но с наибольшей вероятностью составят 80 тыс. руб. Определить прибыль фирмы.